Loss Function
= objective function, cost function
Linear classification에서 말했듯이 최적의 W를 찾기 위하여 만든 W가 좋은지 나쁜지 정량화할 방법이 필요한데 이 때, loss function은 그 역할을 한다.
Low loss = good classifier
High loss = bad classifier
loss를 구하는 방법
- SVM
- Cross Entropy(Softmax loss)
Cross Entropy
- Softmax loss, multinomial logistic regression(다항 로지스틱 회귀)
- unnormalized log probabilities of the classes. 클래스의 정규화되지 않은 로그 확률입니다.
- 스코어 자체에 추가적인 의미를 부여한다.
- 스코어를 가지고 클래스 별 확률 분포를 계산
- softmax function : 스코어들에 지수를 취해서 양수가 되게 만든다. 그리고 그 지수들의 합으로 다시 정규화시킨다. 그래서 softmax함수를 거치게 되면 확률분포를 얻을 수 있고 그것은 바로 해당 클래스일 확률이 되는 것이다. 확률이기 때문에 0에서 1사이의 값이고 모든 확률들의 합은 1이 된다.
- loss = -log(정답클래스확률)
- loss함수는 얼마나 좋은지가 아니라 얼마나 안 좋은지를 측정하는 것이기 때문에 log에 마이너스를 붙인다.

(조건부확률)X = xi일 때, Y가 k라는 클래스에 속할 확률로 계산한다. 이 식은 likelihood 구조가 된다.
밑에 식은 모든 클래스에 대한 스코어 값의 합이다. 위에는 k클래스에 대한 스코어값이다.
아래는 실제로 대입해본 결과이다.

- 스코어를 지수화 -> 합이 1이 되도록 정규화 -> 정답스코어에만 -log를 씌어줌
Question
What is the min/max possible loss Li?
loss function이 어떤 최소, 최대값을 가질 수 있나?
최솟값 = 0, 최댓값 = 무한대
최솟값 : 클래스에 대해 제대로 예측하게 되면 확률이 1이 되는데, 이 1값이 negative log로 들어가기 때문에 (-log1 = 0) 0이 되게 된다. 이 특징은 SVM과 똑같다.
정답클래스에 대한 log확률이기 때문에 -log(1) = 0이 된다. 그래서 완벽히 분류했다면 loss는 0이 될 것이다.
loss가 0이 되려면 실제 스코어는 어떤 값이어야 할까?
정답스코어는 극단적으로 높아야할 것이다. 거의 무한대에 가깝게. 지수화를 하고 정규화를 하기 때문에, 확률1(정답)과 그외 0을 얻으려면 정답클래스 스코어에는 +무한대가 되어야하고, 나머지는 -무한대가 되어야한다.
Usually at initialization W are small numbers, so all s~=0. What is the loss?
만약 스코어 모두 0과 가까운 수를 가지면, 이 경우 loss는 어떻게 될까?
스코어가 0이면 e의 0승이 되기 때문에 정규화되지 않은 확률은 각 클래스마다 1이 되고
결국 -log(1/class수)가 된다.
Multiclass SVM
- hinge loss
- multiclass Support Vector Machine
- 스코어 자체가 실제로 의미하는 것보다 정답클래스가 정답이 아닌 클래스들보다 더 높은 스코어를 내기를 원함
x𝑖=이미지, y𝑖=이미지가 어떤 클래스인지를 나타내는 정수 값
scores vector : s = f(x𝑖, W) : 입력이미지인 x𝑖와 학습하고자하는 가중치 W의 함수로 나타낼 수 있다.

j = 정답이 아닌 케이스에 대해 하나씩 반복하게 된다.
s𝑗= 오답일 때 스코어
s𝑦𝑖 = 정답일 때 스코어
1 = SVM의 마진

추정값과 정답 사이의 차이의 마진을 반영하고 이 값과 0을 비교하여 더 큰 값을 해당 클래스에 대한 loss로 정의한다. 마진보다 작은 스코어의 크기 변화는 loss에 대해 영향을 주지 않는다.
각 정답이 아닌 클래스마다 반복하면서 정답을 얼마나 못맞췄는지 계산한 다음 전체 학습데이터 수만큼 나눠줘서 평균을 구한다. 이 값이 loss값이 된다.
예)


그래서 최종 해당 분류기의 loss 값이 4.6이 됨을 알 수 있다.
Question
What happens to the loss if the scores for the car image change a bit?
car 스코어가 조금 변하면 loss에는 무슨 일이 일어날까?
car 스코어가 조금 바뀌더라도 loss는 바뀌지 않을 것이다.
loss는 오직 정답스코어와 그 외의 스코어와의 차이만 고려했다. 따라서 이경우에는 car스코어가 이미 다른 스코어들보다 엄청 높기 때문에 스코어를 조금 바꾼다해도, 서로간의 margin은 여전히 유지될 것이고, 결국 loss는 변하지 않고 0일 것이다.
what is the min/max possible loss?
loss가 가질 수 있는 최솟값, 최댓값은?
정답에 가까울수록 loss값은 0에 가깝고(식 자체가 0을 포함한 max()이므로), 많은 오답이 발생할 경우 무한대값까지 가질 수 있다.
If all the scores were random, what loss would we expect?
만약 모든 점수가 무작위로 나온다면, loss는 어떻게 될까?
what if the sum was instead over all classes?(including j=y𝑖)
합계가 모든 클래스에 대해 대신 있다면 어떨까? 정답인 경우까지 포함해서 loss를 계산하면 어떻게 될 것인가?
우리는 정답인 경우를 빼놓고 loss를 계산했었다.
정답인 경우를 식에 대입해보면(그림상 cat) max(0, 3.2-3.2+1)로 결국 1이 나오기 때문에 loss에 1이 더 증가할 것이다. 굳이 넣을 필요가 없다.
What if the loss used a mean instead of a sum?
합계 대신 평균을 사용한다면?
답은 영향을 미치지 않는다이다. 클래스의 수는 어차피 정해져 있으니 평균을 취한다는건 그저 loss function을 리스케일할 뿐이다.(단지 스케일만 변하는 것뿐)
자유롭게 결정하면 된다. 우리의 목적은 W의 loss를 최소화하는데 있기 때문에 크게 상관이 없다.
what if we used? 제곱을 사용하면 어떨까? 같은 결과가 나올까?
결과는 달라질 것이다. 좋은 것과 나쁜 것 사이의 트레이드 오프를 비선형적인 방식으로 바꿔주는 것이다. 그렇게 되면 loss함수의 계산 자체가 바뀌게 된다. 이 경우에는 squared hinge loss라고 부르고, 특정 데이터셋에서는 squared hinge loss가 더 좋은 성능을 보이는 경우가 있다고 한다.둘 중 어떤 loss를 선택하느냐는 우리가 에러에 대해 얼마나 신경쓰고 있고, 그것을 어떻게 정량화할 것인지에 달려있다.
- 다른 답안
제곱을 하면 none liner해서 차이는 생기지만 결과에는 영향이 없다. 그렇다면 굳이 수를 커지게 해서 bit를 많이 쓸 필요가 없다.
usually at initialization W are small numbers, so all s ~= 0 What is the loss?
만약 스코어 모두 0과 가까운 수를 가지면, 이 경우 loss는 어떻게 될까?
클래스의 개수 -1 이 된다.
loss를 계산할 때 정답이 아닌 클래스를 순회한다. 그러면 (클래스-1)클래스를 순회할 것이다. 비교하는 두 스코어가 거의 비슷하니 답은 클래스의 개수 -1 이 된다.
운이 좋게도 W가 0인 정답을 찾았다면, Loss가 0이 되게 하는 W가 유일하게 하나만 존재할까?
아니다. 다른 W도 존재한다. W의 스케일은 변하므로 W에 두배(2W)를 한다고 해도 변하지 않을 것이다.
Example code
def L_i_vectorized(x, y, W):
delta = 1.0 # margin
scores = W.dot(x)
margins = np.maximum(0, scores - scores[y] + delta) # loss
margins[y] = 0
loss_i = np.sum(margins)
return loss_iWeight Regularization
그럼 학습데이터를 제외하고 어떤 W값이 좋은가?라는 의문점이 생긴다. 그래서 나온 개념이 Weight Regularization이다.
- Regularization : 모델이 트레이닝 데이터셋에 완벽히 핏하지 못하도록 모델의 복잡도에 패널티를 부여하는 방법
- Regularization 참고

람다 : 얼마나 세게 Regularization할건지 정하는 파라미터
이 텀을 너무 세게 하면 람다 앞부분의 트레인 성능이 줄어들 수 있다. 하지만 트레인 성능이 줄어들더라도 테스트셋을 만났을 때 테스트 성능이 더 좋아질 수 있다.
(만약 너가 복잡한 모델을 계속 쓰고싶으면, 이 패널티를 감수해야할거야!)
function 종류
- L2 reqularization
- 가중치 행렬 W의 Euclidean Norm에 패널티를 주는 것
- 위 이미지에서 w1보다 w2를 더 선호할 것이다. 왜냐하면 w1은 2-4번째가 다 0이기 때문에 0에 매칭되는 x의 인풋값들이 무시되기 때문이다. (w2가 더 norm이 작기 때문)
- L2는 분류기의 복잡도를 상대적으로 w1과 w2 중 어떤 것이 더 거친지를 측정한다.(값이 매끄러워야함) 즉, 모든 요소가 영향을 주는 것을 원한다.
- L1 reqularization
- 가중치 W에 0의 개수에 따라 모델의 복잡도를 다룬다.
- Elastic net(L1+L2)
- Max norm reqularization
- Dropout
SVM vs Cross-Entry
score func = Wx+b 로 정의할 수 있다.

SVM
- 정답스코어와 정답이 아닌 스코어간의 마진에 신경씀
- 일정 선(margins)을 넘기만 하면 더이상 성능개선에 신경쓰지 않는다.
Softmax
- 확률을 구해서 -log(정답클래스)
- 정답스코어가 충분히 높고, 다른 클래스스코어가 충분히 낮은 상태에서도 최대한 정답 클래스에 확률을 몰아넣으려고 할 것이고, 정답클래스는 무한대로, 그외의 클래스는 음의 무한대로 보내려할 것이다.
- 성능을 더 높이려할 것이다.
1.

데이터의 한 점이 있는데 이 점이 조금씩 이동하는 경우가 있을 때 스코어 값도 영향을 받게 된다. 이때 각각의 loss function은 어떻게 될까? SVM같은 경우에는 식에서 정의한 마진(1)보다 변화량이 작을 때는 실제 loss값은 변화가 없다. 반면 cross는 분모, 분자 모두 전체적으로 영향을 받기 때문에 많이 진동하는 현상을 확인할 수 있다.
2.
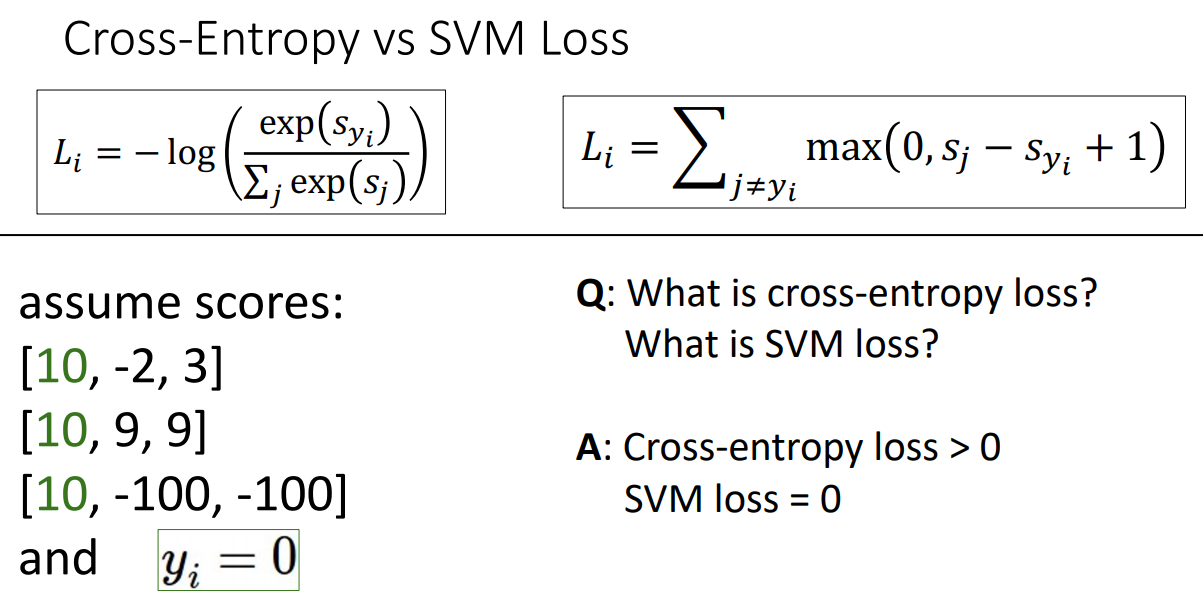
3.
마지막 데이터 포인트의 점수를 약간 변경하면 각 손실이 어떻게 됩니까?
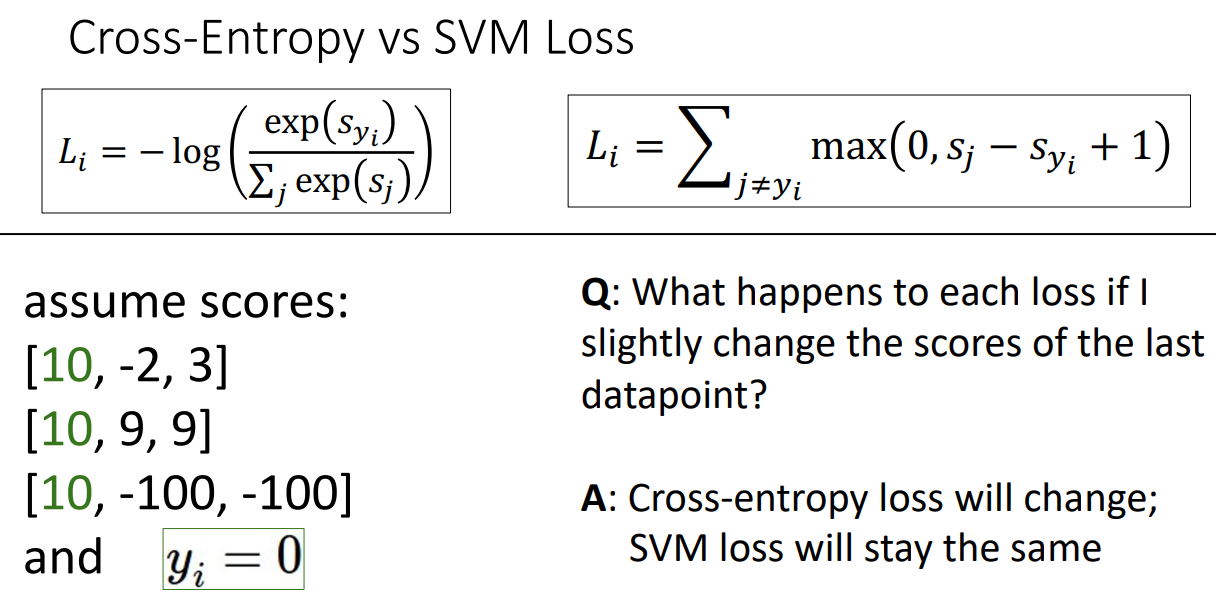
cross-entry loss는 변경되고, SVM loss는 그대로 유지된다.
4.
10점에서 20점으로 점수를 두 배로 올리면 각 loss는 어떻게 됩니까?

cross-entry loss는 감소하고, SVM loss는 여전히 0이다.


- full loss - loss function + lambda(Weight Regularization) : 복잡함과 단순함을 통제하기 위해 loss func에 reqularization term추가


