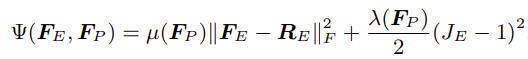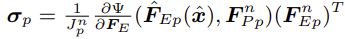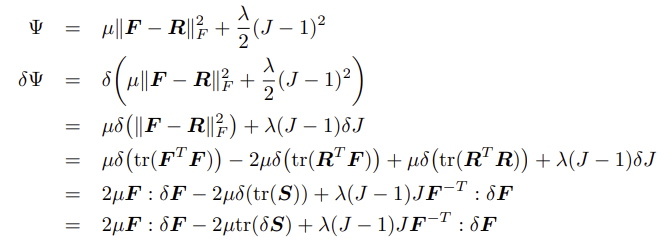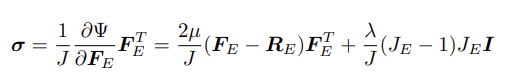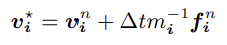Summury

MPM snow simulation에서 3,4번째 단계인 "Compute grid force & Update grid velocity"를 수행하기 위한 개념과, 코드 구현 방식 설명

---

개념

1. $Fˆ_{Ep}(xˆ)$

임의의 node index $i$에 대한 좌표상 위치 $x_i$는 다음을 만족한다.

$xˆ_i=x_i + ∆tv_i$


또한, $xˆ_i$에 대한 탄성 deformation gradient $Fˆ_{Ep}$는 [Sulsky et al. 1995]에 의해 다음을 만족한다.

$Fˆ_{Ep}(xˆ) = (I + Σ_i (xˆ_i - x_i) (∇w_{ip}^n)^T ~ )F_{Ep}^n$

이때, 논문의 full method에서는 $xˆ_i=x_i$라고 한 뒤, force를 계산하라 하였으므로, $Fˆ_{Ep}(xˆ) = F_{Ep}^n$ 이다.
( Eulerian grid node에서의 위치 $xˆ_i$인데, 이 grid는 움직이지 않으므로 위치의 변형이 일어난다고 생각하지 않는다, 따라서 $xˆ_i=x_i$)

---

2. 탄성-소성 energy density 함수 $Ψ(F_E, F_P)$

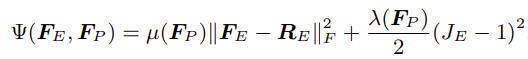
∵ $µ(F_P) = µ^0e^{ξ(1-J_P)}$ , $λ(F_P)=λ^0e^{ξ(1-J_P)}$, $J_P = det(F_P), J_E=det(F_E)$

polar decomposition을 통해 $F_E= R_E S_E$로 분해가 가능하고, $R_E = UV^T$이다.
($U,V$는 $F_E$를 "polar SVD"한 것)

---

3. CauchyStress "σ"

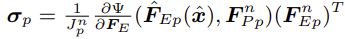
여기서 $Fˆ_{Ep}(xˆ)$는 1번에서 언급한대로 이 논문에서 $Fˆ_{Ep}(xˆ) = F_{Ep}^n$ 이고,

$\frac{∂Ψ}{∂F_E} (F_{Ep},F_{Pp}^n)$를 구하는 식은 다음과 같이 변형 가능하다.

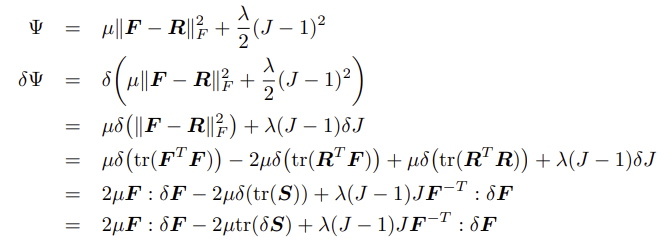
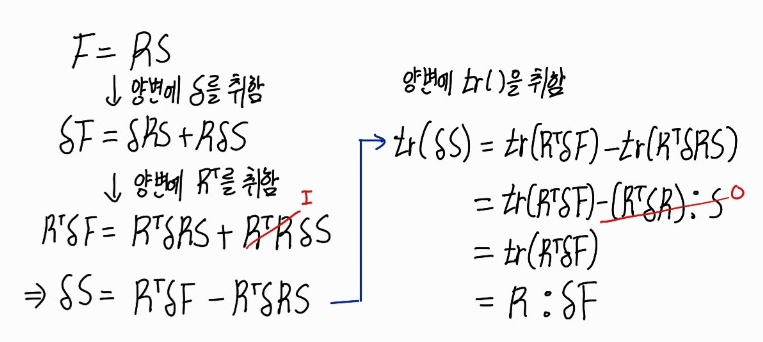
※ tr : 행렬의 주대각 성분들의 합

이렇게 구한 $tr(δS)$을 위의 $δΨ$식에 넣으면 $\frac{∂Ψ}{∂F_E}$를 구할 수 있음.

---

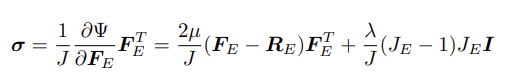
4. Force $f_i(xˆ)$ from elastic stress

탄성 응력으로 발생한 node index $i$에서의 force $f_i(xˆ)$는 다음과 같다.

$-f_i(xˆ) = \frac{∂Φ}{∂xi}(xˆ) = Σ_p V_p^0 \frac{∂Ψ}{∂F_E} (Fˆ_{Ep}(xˆ),F_{Pp}^n) (F_{Ep}^n)^T ∇w_{ip}^n$

이때, $σ_p = \frac{1}{J_p^n} \frac{∂Ψ}{∂F_E} (Fˆ_{Ep}(xˆ),F_{Pp}^n) (F_{Ep}^n)^T$ 이고, $V_p^n = J_p^nV_p^0$이므로

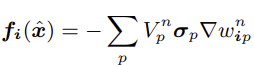
따라서 3번에서 구한 CauchyStress "σ"식을 이용하여 Force $f_i(xˆ)$를 구할 수 있음.

---

5. Update velocities on grid ($v^*$)

논문의 식에 의해서 update할 속도 $v^*$는 다음을 만족한다.

---

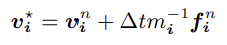
In code

이전 단계에서 각 paticle의 density, volume 초기값은 계산되어 저장되었고, 각 node의 mass, 힘이 적용되기 전의 velocity가 계산되어 저장되었다.
이 값들을 이용하여 grid의 force를 계산하고, 이 힘이 적용된 $v^*$값을 계산한다.

1. computeGridForce()

• 각 particle의 bound 안에 있는 node의 force를 계산하는 함수.
• 위의 개념 4에서 설명한 것과 같이 각 particle의 부피 V와 CauchyStress σ를 한 값을, particle이 속한 node를 돌면서 가중치의 gradient를 곱해 node의 force에 더함.
• 추가적으로 중력가속도 9.8을 node의 질량과 곱하여 y축의 음수방향으로 곱하여 힘을 추가

2. updateGridVelocity()
   모든 node를 돌면서 해당 node의 속도 v를 개념 5의 식과 같이 더함.
   여기서 ∆t는 미리 정한 constant 값.

---

추가할것

polar decomposition 개념
Lame perameter?