해당 논문은 2018년 4월, Deepmind에서 나온 논문으로 Vector Quantised Variational AutoEncoder, VQ-VAE 라고 부르는 모델을 소개한다.
기존 VAE와 Vector quantisation을 접목해 나온 method라고 생각하면 될것 같다.
논문에서 스펠링 보고 헷갈렸는데 찾아보니 영국식 영어로 learnt, quantised를 사용하고 있다.
Variational AutoEncoder (VAE)
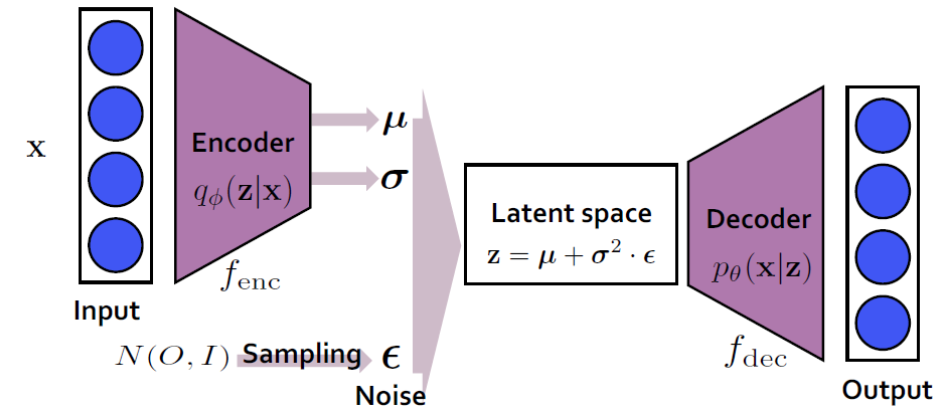기존 VAE같은 경우 위와 같은 구조를 갖고있는데 input을 encoder를 통해 input x 에대해 latent vector z의 분포 (mean, std)를 예측하는 형태이다. 즉 encoder는 q(z|x)를 approximate하는 것을 목표로 한다. decoder같은 경우 latent vector를 통해 input으로 변환하는 과정을 하게된다. encoder과는 반대로 p(z|x)를 approximate하는 것을 목적으로한다. z를 통해 x를 생성하는것으로 `generate model`이라고 한다. mean, std로 복원을 하게 된다면 decoder에서 항상 같은 x를 뽑아내기에 latent space에서 noise epsilon을 추가해줘 약간의 변화를 준다.
VAE를 자세히 살펴보면 재미있는 과정이 많다. 확률 분포를 어떻게 approximate하고 loss를 계산할 것인가에 대해 수학적으로 접근하고 해석하는 것이 있는데 나중에 정리해볼까 한다.
Vector Quantised VAE
그럼 이제 VQ-VAE를 살펴보자. 논문의 Abstract 를 보면 Vector Quantised 를 이용하면 VAE에서 발생할 수 있는 posterior collapse (여러 이유가 있지만 하나의 원인으로 powerful decoder에 의해 발생할 수 있는 것으로 input에 상관없이 즉, condition과 상관없이 sequence를 생성하는 문제이다.)를 해결할 수 있다고 한다.
그래서 Vector Quantised가 뭔데?
처음에 이 단어를 들었을때 quantised를 생각해 차원을 양자화하는 건가? 어떤 method인지 감이 안잡혔다. 찾아보니 양자역학과 같은 간지나는 기술은 아니고 Continuous space 데이터를 Discrete space로 representation하는 기술이다. 어떤 식으로 할까 생각하면 그냥 간단하게 continuous space를 잘게잘게 잘라 대표적으로 여러 Codebook으로 mapping하는 간단한 기술이다.
그냥 봤을때는 KNN이랑 크게 달라보일게 없어보인다. 이름만 바꿔서 멋있게 포장한것 같다...
그래서 quantisation을 사용하면 왜 posterior collapse가 해결된다는 걸까?
기존 VAE에서는 input x 에대해 사전 분포 (gaussian distribution)으로 예측하는데 그래서, VAE에서 학습과정에서 KL발산 항을 통해 정규분포를 따르도록 유지한다. 그런데 VQ-VAE에서는 continous space에서 codebook으로 양자화를 진행하면서 input x에대해 여러 이산 벡터들로 예측하는 차이가 있다. 이로써 특정 분포로 수축시키려는 압력이 사라지고 KL 발산 항을 필요하지 않아 위 문제를 해결할 수 있다.
더 자세한 내용은 posterior collapse가 발생하는 이유를 찾아보면 좋을 것 같다.
VQ-VAE의 전체적인 구조는 다음과 같이 생겼다.
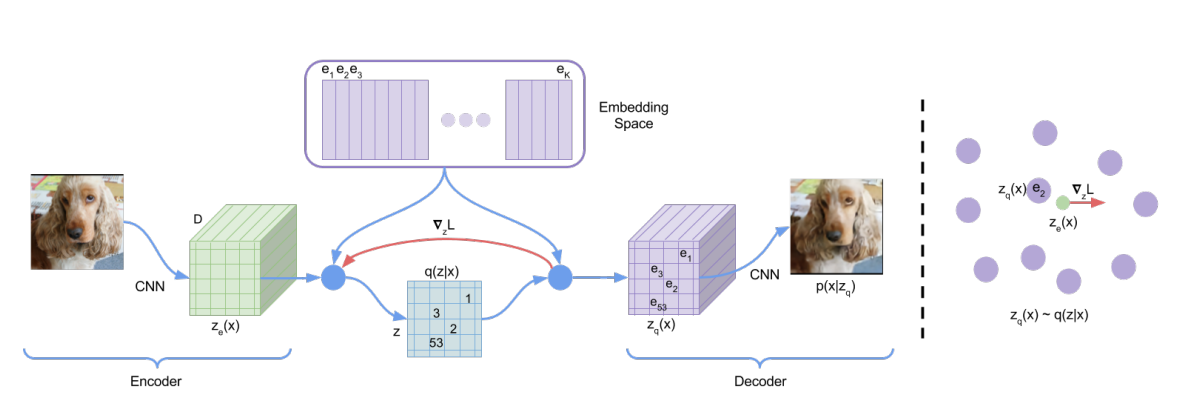
loss는 어떻게 계산되는데?
total loss = reconstruction loss + embedding loss + commitment loss
참고로 헷갈릴만한 요소로 ze(x) 는 encoder로 continous vector space를 가지고 zq(x)는 decoder에서 사용하는 것으로 ze(x)의 값을 가장 가까운 codebook으로 매핑한 값이다.
신기한 점은 reconstruction loss는 zq에 대해 적용하고 ze에는 stop gradient를 적용하고 codebook e에 l2 loss를 적용하고 있다.
log p(x) = log (sigma p(x|zk)p(zk))
p(x) >= log p(x|zq(x))p(zq(x)) (jensen's enquality)
decoder에서 z = zq(x) 를 만족하는 z에만 확률을 할당하는 것이고 z != zq(x) 일경우에는 p(x|z)를 0에 근사한다. prior 확률 p(z)에 대해서는 논문에서는 catergorical distribution으로 동일확률분포를 사용해 학습후 추후에 autoregressive model을 사용해 image, audio데이터에 적용했다고 한다. p(z)를 VQ-VAE와 같이 학습할 수 있다면 더 좋아질 수 있는 여지를 남겨두었다.
VQ-VAE를 처음 봤을때 모델을 경량화하고 실시간으로 적용할때 좋겠다고 생각이 들었지만 hyper parameter에 민감하고 단순히 봤을때 optimal한 값을 찾기에는 좋은 구조는 아닌것 같다고 생각이 들었다. task에 따라 VQ-VAE로도 충분히 잘 작동할 환경이라면 적용하는데 이점은 클것같아 보인다.
생각나는 다음에 다룰 것들...?
- GameNGen: Diffusion Models Are Real-Time Game Engines
