[알고리즘] 에라토스테네스의 체 - 소수(Prime Number)

소수 판별 알고리즘

소수란 1보다 큰 자연수 중에서 1과 자기 자신을 제외한 자연수로는 나누어 떨어지지 않는 자연수이다. 보통은 2부터 N-1(자신-1)까지 돌며 나누어 떨어지는 수가 있는지 확인한다.

어떤 수의 약수는 그 수의 제곱근을 기준으로 곱셈 연산에 대해 대칭을 이룬다. 이런 성질로 인해 어떤 수의 2부터 제곱근까지만 나누어 떨어지는 수가 있는지 확인하면 된다.

💡에라토스테네스의 체 알고리즘이란?

에라토스테네스의 체(Sieve of Eratosthenes)는 N보다 작거나 같은 모든 소수를 찾을 때 사용하는 알고리즘이다.

• 에라토스테네스의 체 동작 과정
  • 2부터 N까지의 모든 자연수를 나열한다.
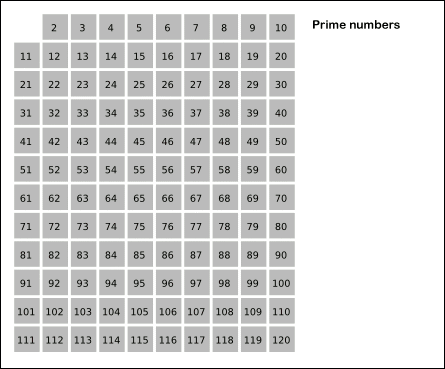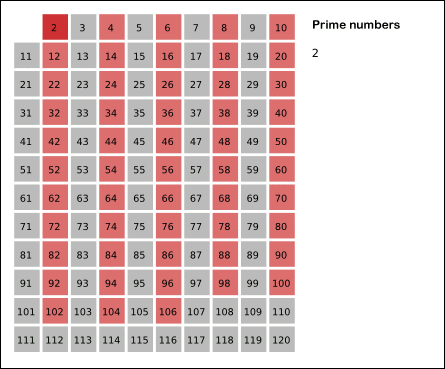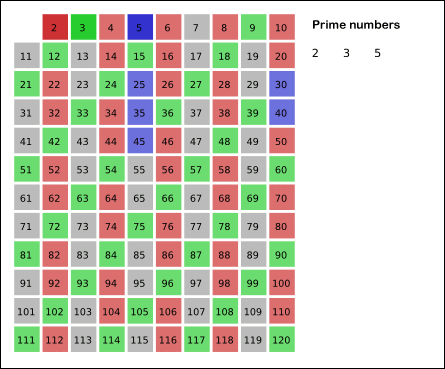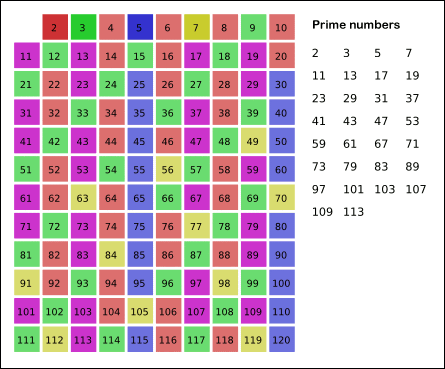
  • 2부터 시작하여 n의 제곱근 까지 돌며, 그 수의 배수에 해당하는 수를 모두 지운다. 지울 때 자기 자신은 지우지 않고, 이미 지워진 수는 건너뛴다.
  • 순회를 다 돌고 남아있는 수를 모두 출력한다.

import math

a=int(input()) # a보다 작거나 같은 소수를 구할 것임
answer=[]
check=[True for i in range(a + 1)]
for i in range(2,int(math.sqrt(a))+1): # 2부터 입력받은 수의 제곱근 까지 모두 확인
    if check[i] == False: continue # 확인하는 값이 이미 제거되었으면 스킵
    for j in range(i+i,a+1,i): # 확인하고자 하는 배수에 해당하는 값을 False
        check[j]=False

# 위에 for문이 끝나면, 소수가 아닌 곳에는 False 체크가 되어 있고
# 소수인 숫자들에는 True 가 남아 있다.

for i in range(2,a+1):
    if check[i]==True:
        print(i,end=' ')

💡에라토스테네스의 체 시간복잡도

• 에라토스테네스의 체는 선형 시간에 가까울 정도로 빠른 O(nlog(logn))이다.
• 하지만 각 자연수에 대한 소수 여부를 저장해야 하므로 숫자가 클 경우 메모리가 많이 필요하다.