Today What I Learned

Javascript를 배우고 있습니다. 매일 배운 것을 이해한만큼 정리해봅니다.

1. Data Structure - Stack

1. Stack은 어떻게 생겼나?

1) 그림으로 그려보자.

먼저 내가 그린 그림

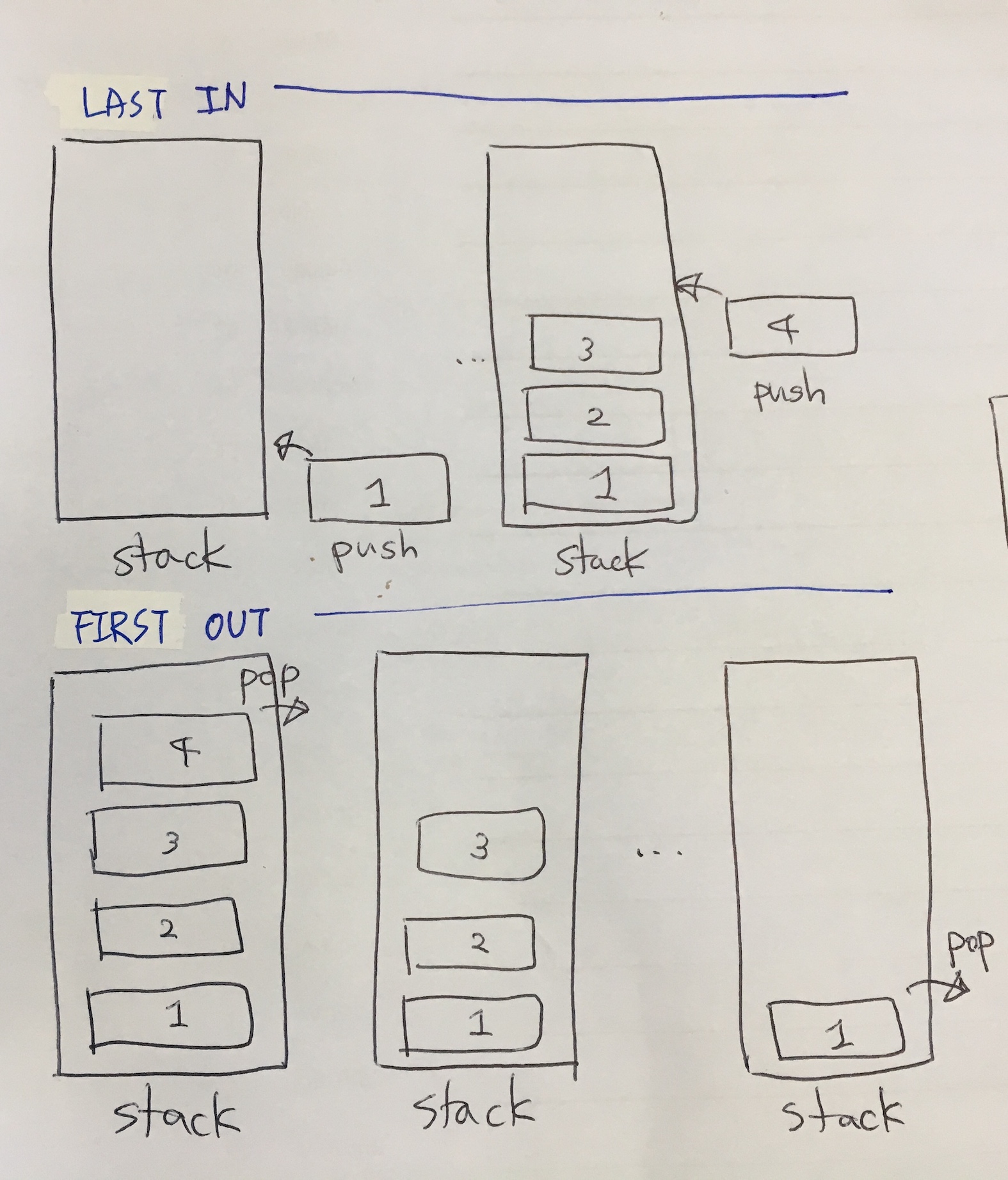
좀 더 나은 그림으로...

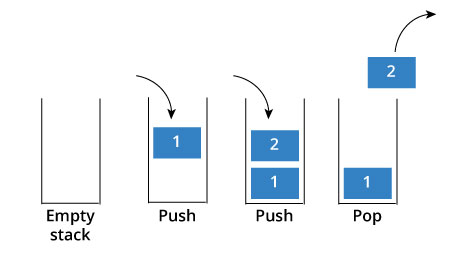
[그림 출처: https://www.programiz.com/dsa/stack]

2) Stack 구조

• stack은 Last In First Out(후입선출)의 구조을 가지고 있다.
• 빈 stack에 value가 차곡 차곡 순서대로 쌓이고, value를 제거할 때에는 가장 마지막에 쌓였던 것부터 뒤에서부터 제거된다.
• 실생활에서 예시를 떠올리다 보니 택배상하차 모습이나 만원 버스에 가장 마지막으로 문 앞에 탔다가 맨 처음 내리는 내 모습이 떠올랐다.
  브라우저에서의 예시는 '돌아가기 버튼'이 stack 구조 중 하나이다.
• stack은 tree 구조 검색 시 깊이우선검색(Depth First Search: 한 노드의 끝까지 탐색한 후 옆으로 이동하는 방식)에서 사용된다.

2. Stack의 property와 method

1. Property of Stack
   • top point: stack의 가장 상단 위치
2. Method of Stack
   • push: 스택에 하나씩 아래에서부터 위로 쌓아줌
   • pop: 스택 가장 상단에서부터 하나씩 아래로 제거해줌
   • peek: 스택 가장 상단 데이터를 리턴
   • empty: 빈 스택인 경우 true, 아닌 경우 false를 리턴
   • swap: 스택 가장 상단의 데이터 2개의 위치를 변경
3. Pesuedo Code 짜보기
   • 스택이라는 배열을 선언하고 top point를 0으로 지정한다.
   • push & pop :
     • 배열의 method push와 pop과 같은 형식으로 함수를 마련한다.
     • 데이터가 주어질 때 가장 후반부에 쌓거나 제거하고
     • top point가 +1 혹은 -1 한다.
   • peek: top point 값을 인덱스로 가진 배열의 요소를 리턴한다.
   • empty:
     • 스택이 비어있는지를 확인하기 위해 스택의 길이를 확인하는 함수를 준비한다.
     • 함수는 스택 배열의 길이가 0일 때 true, 그렇지 않을 때는 false를 리턴한다.
   • swap:
     • top point의 데이터를 임시로 담을 변수를 선언한다.
     • top point의 데이터를 임시 변수에 담는다.
     • top point -1 위치의 데이터를 top point에 할당한다.
     • top point -1 위치에는 임시 변수의 데이터를 할당한다.
     • top point와 top point -1 위치의 데이터를 리턴한다.
4. Pesuedoclassical implementation

   const Stack = function() {
    this.storage = {};
    this.count = 0;
   };
   Stack.prototype.push = function(value) {
    this.storage[this.count] = value;
    this.count++;
    return value;
   };
   Stack.prototype.pop = function() {
    if (this.count > 0) {
      const isRemoved = this.storage[this.count];
      delete this.storage[this.count];
      this.count--;
      return isRemoved;
    } else {
      return;
    }
   };
   Stack.prototype.size = function() {
    return this.count;
   };

2. Data Structure - Queue

1. Queue은 어떻게 생겼나?

1) 그림으로 그려보자.

여기도 내가 그린 그림부터...

좀 더 나은 그림으로

[그림 출처: https://www.programiz.com/dsa/queue]

2) Queue 구조

• queue은 First In First Out(선입선출)의 구조을 가지고 있다.
• 빈 queue에 value가 차곡 차곡 순서대로 쌓이지만 value를 제거할 때에는 가장 먼저 쌓였던 것부터 앞에서부터 제거된다.
• 실생활에서 예시는 그냥 편의점 음료수를 배치할 때가 떠올랐다.
  프로그래밍 중에서는 '프린터에 인쇄 예정인 문서 올리기'가 있다.
• queue는 tree 구조 검색 시 넓이우선검색(Breadth First Search: 노드 레벨에서 좌에서 우로 탐색한 후 다음 노드 레벨로 이동하는 방식)에서 사용된다.

2. Queue의 property와 method

1. Property of Queue
   • locaCount: queue에 쌓인 각각 데이터 개수
   • head: queue의 가장 앞부분에 있는 데이터
2. Method of Queue
   • enqueue: queue head부터 tail 방향으로 하나씩 순서대로 쌓아줌
   • denqueue: queue head부터 tail 방향으로 하나씩 순서대로 제거해줌
   • peek: queue front 데이터를 리턴
   • isEmpty: queue에 아무 것도 없는 경우 true, 아닌 경우 false를 리턴
3. Pseudocode 짜보기
   • queue라는 빈 객체를 선언하고 locaCount, head를 0으로 선언.
   • enqueue:
     • 만약 queue가 비어있다면, head를 +1 한다.
     • queue에 locaCount가 key인 value에 주어진 data를 추가하고, locaCount를 +1 한다.
   • dequeue:
     • 만약 head가 0이면 dequeue는 불가능하다.
     • queue에 값이 1개 이상이면(locaCount가 0보다 크면)
       1) head 값을 임시로 저장한다.
       2) queue에서 head -1 값을 key로 하는 값을 delete하고 locaCount를 -1한다.
       3) 그런 다음 head를 임시로 저장한 이전 head 값 +1로 다시 할당한다.
   • peek: queue에서 head -1 값을 key로 하는 값을 리턴한다.
   • isEmpty: locaCount가 0이면 true, 아니면 false를 리턴한다.
4. Pesuedoclassical implementation

const Queue = function() {
  this.storage = {};
  this.start = 0;
  this.end = 0;
};

Queue.prototype.enqueue = function(value) {
  this.storage[this.end] = value;
  this.end++;
  return value;
};

Queue.prototype.dequeue = function() {
  if (this.end - this.start > 0) {
    const isRemoved = this.storage[this.start];
    delete this.storage[this.start];
    this.start++;
    return isRemoved;
  } else {
    return ;
  }
};

Queue.prototype.size = function() {
  return this.end - this.start;
};