Today What I Learned

Javascript를 배우고 있습니다. 매일 배운 것을 이해한만큼 정리해봅니다.

4. Data Structure - Binary Tree

1. Binary Search Tree는 어떻게 생겼나?

1) 그림으로 보자.

Binary Search Tree는 Binary Tree 중 하나이고, Binary Tree는 Tree 구조 중 하나이다.
Tree 구조 보다 모양이 더 깔끔해서 맘에 든다.🙆‍♀️

[출처: https://medium.com/swlh/how-to-solve-a-js-binary-search-tree-problem-585673fc3287 ]

2) Binary Search Tree 구조

• Binary Tree는 Tree 구조이므로 root 노드로부터 시작한다.
  다만 부모 노드 1개에 자식 노드 최대 2개의 구조로 파생되어 가는 자료 구조이다.
  • Root: Binary Tree의 가장 상단에 있는 노드이다.
  • Parent Node: 다른 노드의 부모가 되는 노드이다.
  • Child Node: 부모 노드를 가진 노드이다.
    • left child: 왼쪽에 배치한 자식 노드를 가리킨다.
    • right child: 오른쪽에 배치한 자식 노드를 가리킨다.
• GIF로 보이듯 노드에 담긴 data는 정렬되어 어떠한 위치로 찾아간다. 즉, 노드에 담긴 data는 정렬 기준에 따라 그 위치가 정해진다.
• Binary Search Tree의 정렬 순서
  • 가장 작은 숫자는 가장 왼쪽에, 가장 큰 숫자는 가장 오른쪽에 위치
  • 어떤 숫자가 주어지면 root 노드와 비교하여 작을 경우 왼쪽, 클 경우 오른쪽으로 방향을 정해 계속해서 노드와 숫자를 비교해 그 자리를 찾아간다.
  • 왼쪽 자식 노드는 부모 노드보다 작고, 오른쪽 자식 노드는 부모 노드보다 크다고 볼 수 있다.
• Binary Search Tree의 탐색 속도: 부모 노드를 기준으로 절반의 노드를 고려하지 않고 다른 절반의 노드에서 재귀적으로 탐색하기 때문에 전체 노드를 고려하여 검색하는 것보다 속도가 빨라진다.
  
• Binary Search Tree의 종류
  • Full Binary Tree(포화 이진 트리): 자식 노드가 각각 2개씩 가득 찬 상태
  • Complete Binary Tree(완전 이진 트리): 왼쪽 자식 노드부터 채워가면서 자식 노드가 다 차 있는 상태
  • 편향 이진 트리: 모든 노드들이 한 방향으로만 자식노드를 가짐
• Binary Search Tree 순회 방식
  • 전위: 자신 -> 왼쪽 -> 오른쪽
  • 중위: 왼쪽 -> 자신 -> 오른쪽
  • 후위: 왼쪽 -> 오른쪽 -> 자신

2. Binary Search Tree의 property와 method

1. Property of Binary Search Tree
   • node: 노드(left, value, right 로 구성)
   • sub tree: 부모 노드 속 자식 노드들
   • level & height: 노드의 깊이, 높이
2. Methods of Binary Search Tree
   - insertNumberNode: 숫자로 된 노드를 삽입
   - removeNumberNode: 숫자로 된 노드를 삭제
   - contains: 해당 노드가 존재하는지 검색(children을 찾기 때문에 재귀가 적용)
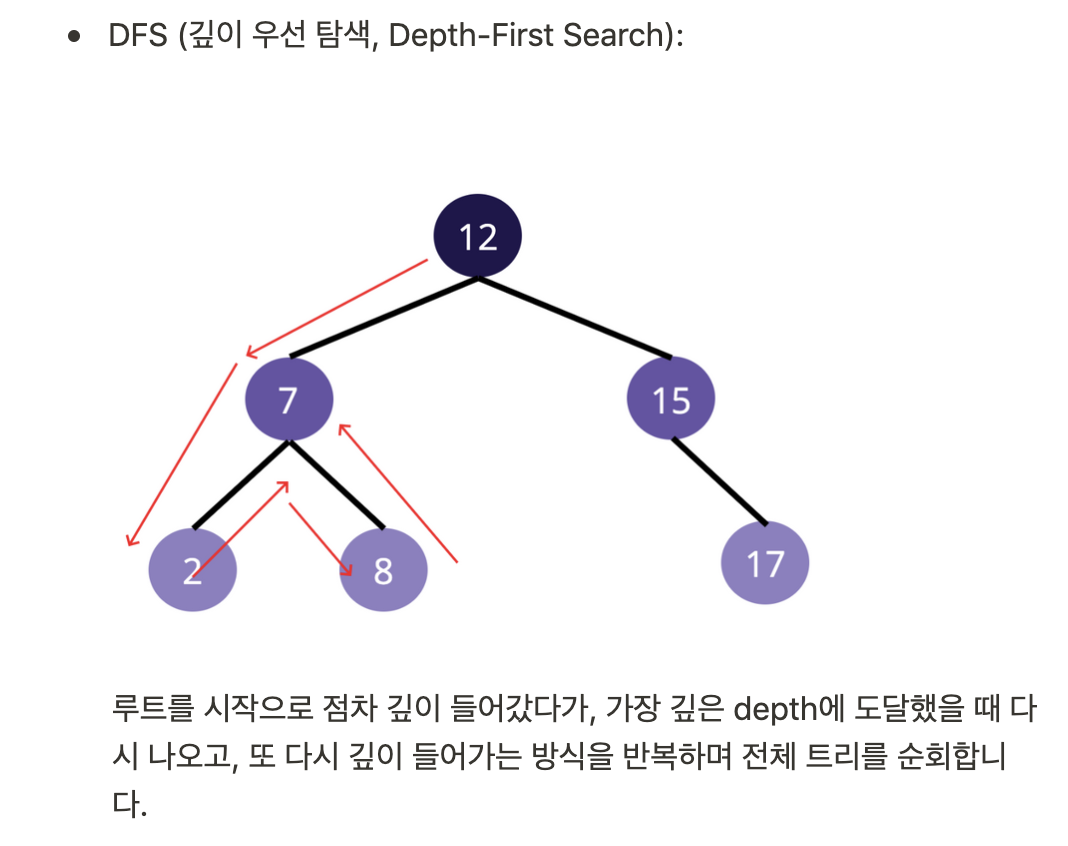
   - Depth-First Search(깊이 우선 탐색 - DFS): 루트에서부터 하단의 노드로 수직적으로 들어가면서 노드마다 callback 함수에 의해 값 변경
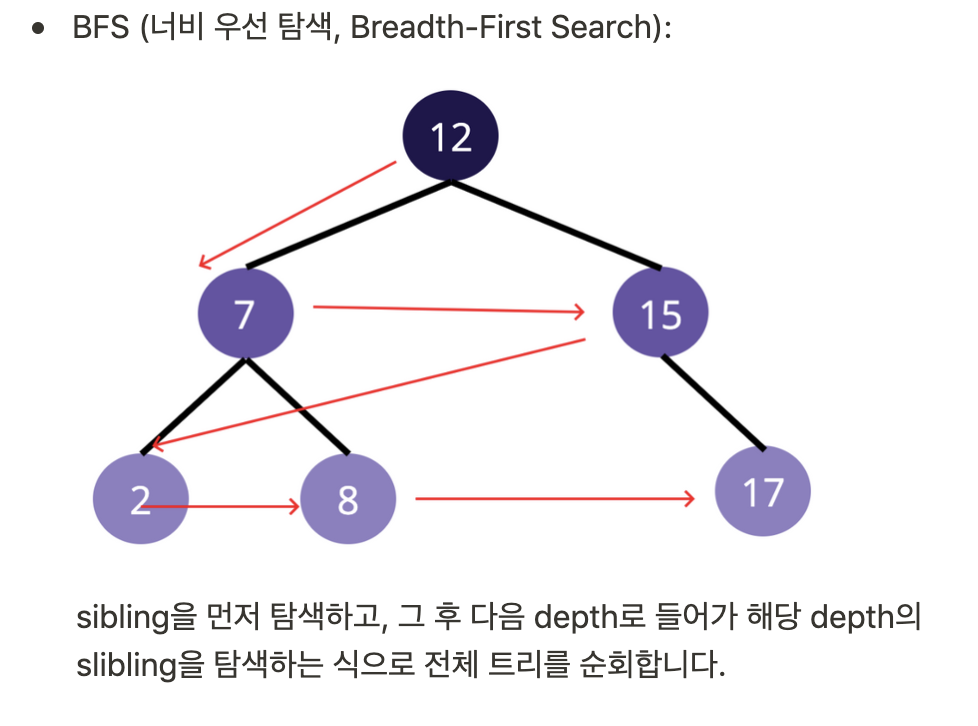
   - Breadth-First Search(너비 우선 탐색 - BFS): 루트에서부터 수평적인 레벨의 노드를 지나 하단의 노드들을 수평적으로 돌면서 callback 함수에 의해 값 변경
   
   
3. Binary Search Tree 관련 읽어보기
   • How Binary Search Trees work in JavaScript: https://medium.com/javascript-in-plain-english/binary-search-tree-in-javascript-ca5aa7ba05de
4. Pseudoclassical Implementation

const BinarySearchTree = function(value) {
  this.value = value;
  this.left = null;
  this.right = null;
}

BinarySearchTree.prototype.insert = function(val) {
  if(val < this.value) {
    if(this.left === null) {
      this.left = BinarySearchTree(val);
    } else {
      this.left.insert(val);
    }
  } else if(this.value < val) {
    if(this.right === null) {
      this.right = BinarySearchTree(val);
    } else {
      this.right.insert(val);
    }
  }
};

BinarySearchTree.prototype.contains = function(val) {
  if(val === this.value) {
    return true;
  }
  if(val < this.value) {
    return !!(this.left && this.left.contains(val));
  }
  if(this.value < val) {
    return !!(this.right && this.right.contains(val));
  }
};

BinarySearchTree.prototype.depthFirstLog = function(callBack) {
  callBack(this.value);
  
  if(this.left) {
    this.left.depthFirstLog(callBack);
  }
  if(this.right) {
    this.right.depthFirstLog(callBack);
  }
};

5. Data Structure - Hash Table

1. Hash Table은 어떻게 생겼나?

1) 그림으로 보자.

정제된 그림으로 보기
[출처: https://bcho.tistory.com/1072]

2) Hash Table 구조

• 개발에 자주 쓰이는 자료 구조이다. 기본적으로 key에 value를 저장하는 데이터 구조이다.
• 크기가 큰 데이터를 저장하기에 좋은 구조이다.
• 위 그림은 전화번호 저장을 예시로 한 그림이다.
  • 이름이 key이고, 전화번호를 최종적으로 bucket에 넣어줘야 한다.
  • 이 때 hash function은 어떠한 규칙에 의해 key 값을 해시 코드(index)로 변환해준다.
    hash function에 의한 해시 코드, 즉 변환 값은 항상 바뀌지 않는다.
  • 변환된 해시 코드(index)를 가지고 해당하는 전화번호는 해당 index의 buckets로 저장되게 된다.
  • 주의할 점은, key 값이 상이하더라도 hash function에 의해 변환된 index가 같은 충돌이 발생할 수 있다. 이를 Hash Collision(해시 충돌)이라 부른다.
    이런 충돌을 해결하기 위해서는 chaining(buckets의 구조를 linked list로 구현)이나 open addressing하는 방법이 있다.
• hash table 자료구조는 비밀번호 암호와와 같은 곳에서 사용된다.
• hash table은 키와 값을 받아 hash function에 넣어 ouput으로 받은 index값을 참조해 스토리지내 해당 index를 가지는 공간(tuple)에 들어가는 과정을 지니고 있다. 아래 그림 참고

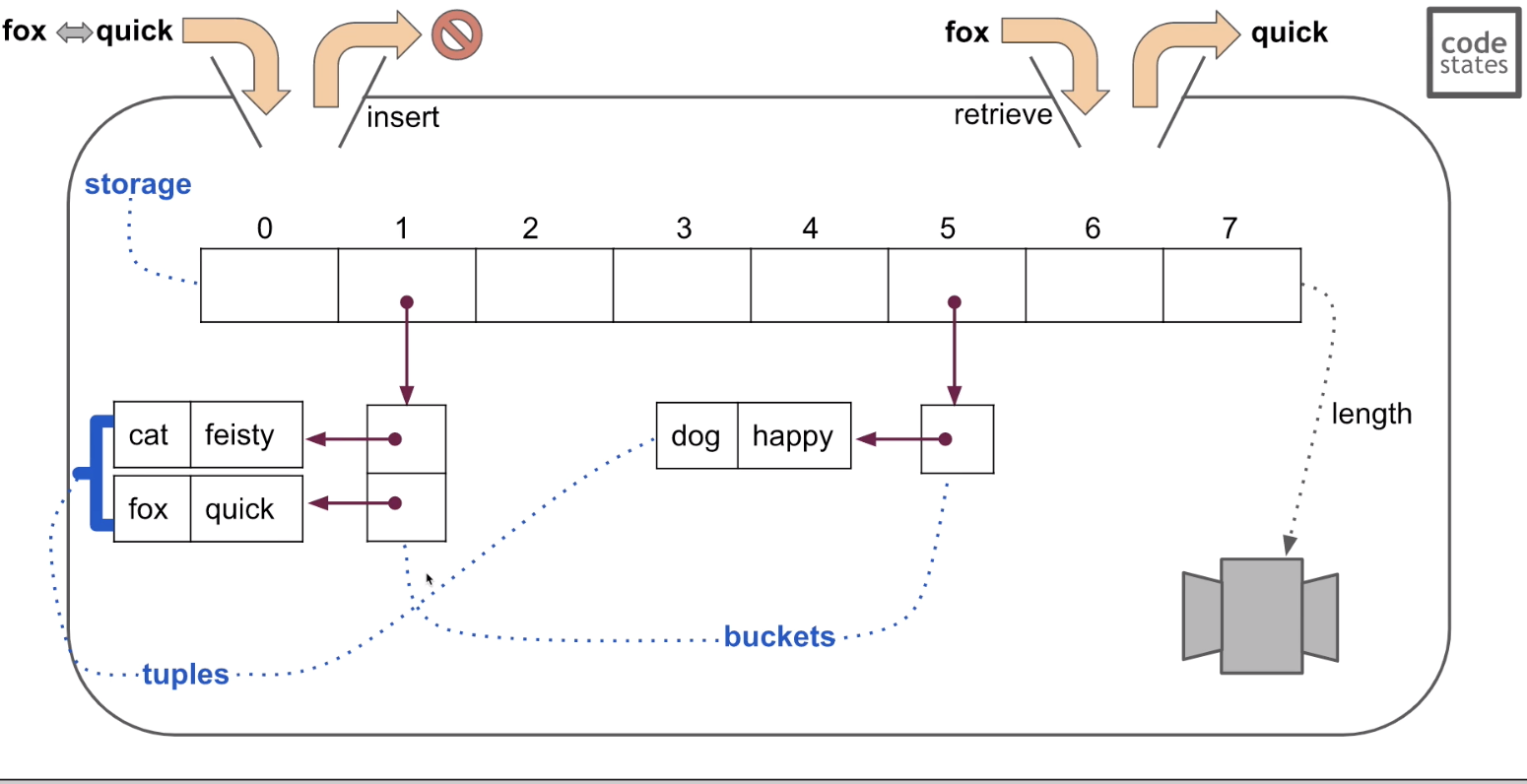
• hash table가 가장 효율적으로 실행될 때는 값이 저장되는 'tuple'과 일정한 사이즈를 받아 운용되는 'storage'의 비율이 25~75% 사이일 때이다. 이렇게 가장 효율적인 형태의 hash table 운영을 위해 만약 비율이 75% 이상이 되는 경우에는 storage의 사이즈를 2배로 증가시키고, 25% 이하인 경우에는 storage를 절반으로 줄이는 작업을 진행해야 하는데 이를 Table Resizing이라고 부른다.
• Table Resizing이 이루어지면 기존 storage의 크기가 달라지기 때문에 새로이 storage를 만들어 이전 storage를 순회하면서 모든 bucket의 tuple 값들을 다시 입력하는 과정이 필요하다. Hash Table은 보통 O(1)의 시간 복잡도를 가지지만 리사이징으로 인해 모든 데이터를 옮기는 이러한 경우에는 O(n)의 시간 복잡도를 나타내기도 한다.

2. Hash Table의 property와 method

1. Property of Hash Table
   • buckets: data를 담을 공간
   • size: buckets에 할당할 사이즈
   • limit: data가 담기는 최대 한계치
2. Methods of Hash Table
   • set: key-value를 저장시킨다.
   • get: key가 주어지면 해당하는 value를 구한다.
3. Hash Table 관련 읽어보기
   • 해쉬 테이블의 이해와 구현 (Hashtable): https://bcho.tistory.com/1072
   • How to implement hash table in javascript: https://reactgo.com/hashtable-javascript/
4. Pseudoclassical Implementation
   • hash table은 모든 function을 처음부터 짜기에 어렵기 때문에 helper function을 받아서 구현.

//Helper Function
const LimitedArray = function(limit) {
  const storage = [];

  const limitedArray = {};
  limitedArray.get = function(index) {
    checkLimit(index);
    return storage[index];  //[0]
  };
  limitedArray.set = function(index, value) {
    checkLimit(index);
    storage[index] = value; //[100]     <<[0] = [100]
  };
  limitedArray.each = function(callback) {
    for (let i = 0; i < storage.length; i++) {
      callback(storage[i], i, storage);
    }
  };
// LimitedArray 함수는 제한된 사이즈를 가진 배열에 접근할 수 있게 해준다.
  
  var checkLimit = function(index) {
    if (typeof index !== "number") {
      throw new Error("setter requires a numeric index for its first argument");
    }
    if (limit <= index) {
      throw new Error("Error trying to access an over-the-limit index");
    }
  };

  return limitedArray;
};
// checkLimit 함수는 배열에서 사용할 인덱스가 전체 한계치를 넘지 않고, 숫자 형식으로 나오게끔 알림을 준다.

// "hashing function"
const getIndexBelowMaxForKey = function(str, max) {
  let hash = 0;
  for (let i = 0; i < str.length; i++) {
    hash = (hash << 5) + hash + str.charCodeAt(i);  //str[3]
    hash &= hash; // Convert to 32bit integer
    hash = Math.abs(hash);
  }
  return hash % max;
}
// 해시테이블에서 사용할 키로 변경해주는 함수이다.: Hash Function이라 부름

이제 Hash Table 구현

const HashTable = function() {
  this._size = 0;
  this._limit = 8;
  this._storage = LimitedArray(this._limit);
}

Hashtable.prototype.insert = function(key, val) {
  const index = getIndexBelowMaxForKey(key, this._limit);
  const bucket = this._storage.get(index) || [];
  
  for(let i = 0; i < bucket.length; i++) {
    const tuple = bucket[i];
    if(tuple[0] === key) {
      const oldValue = tuple[1];
      tuple[1] = value;
      return oldValue;
    }
  }
  
  bucket.push([key, value]);
  this._storage.set(index, bucket);
  this._size++;
  
  if(this._size > this._limit * 0*75) {
    this._resize(this.limit * 2);
  }
  
  return;
};

HashTable.prototype.retrieve = function(key) {
  const index = getIndexBelowMaxForKey(key, this._limit);
  const bucket = this._storage.get(index) || [];
  
  for(let i = 0; i < bucket.length; i++) {
    const tuple = bucket[i];
    if(tuple[0] === key) {
      return tuple[1];
    }
  }
  return ;
};

HashTable.prototype.remove = function(key) {
  const index = getIndexBelowMaxForKey(key, this._limit);
  const bucket = this._storage.get(index) || [];
  
  for(let i = 0; i < bucket.length; i++) {
    const tuple = bucket[i];
    if(tuple[0] === key) {
      bucket.splice(i, 1);
      this._size--;
      
      if(this._size < this._limit * 0.25) {
        this._resize(Math.floor(this._limit / 2));
      }
      return tuple[1];
    }
  }
  return;
}
 
HashTable.prototype._resize = function(newLimit) {
  const oldStroage = this._storage;
  
  newLimit = Math.max(newLimit, 8);
  if(newLimit === this._limit) {
    return;
  }
  
  this._limit = newLimit;
  this._storage = LimitedArray(this._limit);
  this._size = 0;
  
  oldStorage.each(function(bucket) {
    if(!bucket) {
      return;
    }
    for(let i = 0; i < bucket.length; i++) {
      const tuple = bucket[i];
      this.insert(tuple[0], tuple[1]);
    }
  });
});