Today What I Learned

Javascript를 배우고 있습니다. 매일 배운 것을 이해한만큼 정리해봅니다.

---

시간 복잡도 : Time Complexity

• 알고리즘을 수행하는데(컴퓨터가 문제를 풀 때) 최악의 경우에 시간이 얼마나 걸릴지 보여주는 개념이다.
• 그 외 복잡도 분석: 공간 복잡도(space complexity, 알고리즘이 얼마만큼 메모리를 잡아먹는지 보여줌)
• 얼마나 시간이 걸리고 공간을 차지하는 지가 왜 중요한가?
  시간이 오래 걸릴수록, 공간을 많이 차지할 수록 비용 효율적이지 못하기 때문

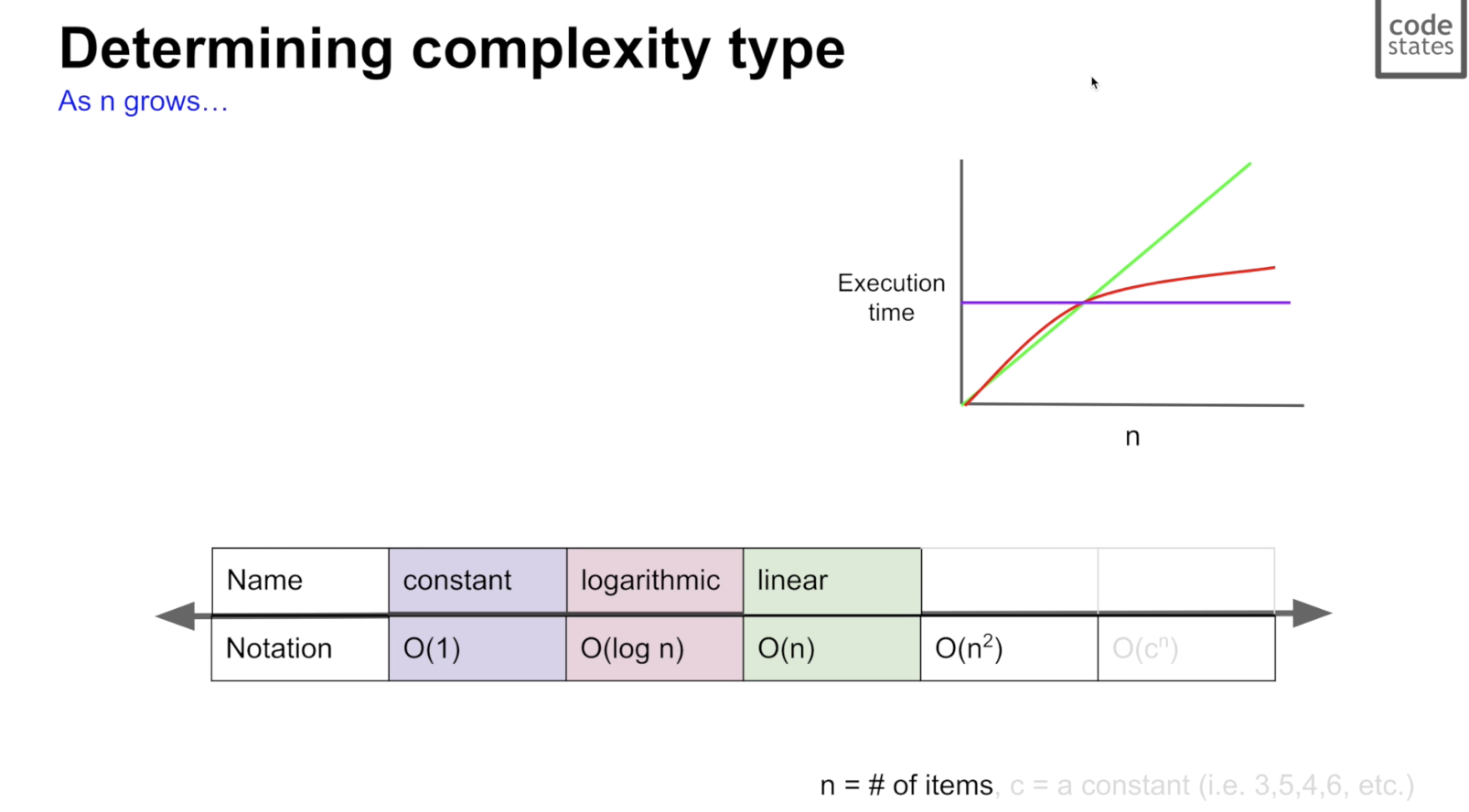
1. Big O 표기법

• 시간 복잡도를 나타내는 방법

• 최악의 경우를 기준으로 정도를 표기한다.
  [출처: 코드스테이츠]

• 좌측은 시간 복잡도가 낮아 시간이 적게 드는 방향, 문제의 규모가 클 수록 느린 폭으로 속도가 줄어든다.

• 우측은 시간 복잡도가 높아 시간이 많이 드는 방향, 문제의 규모가 클 수록 빠른 폭으로 속도가 늘어난다.

2. Big O Notation 종류

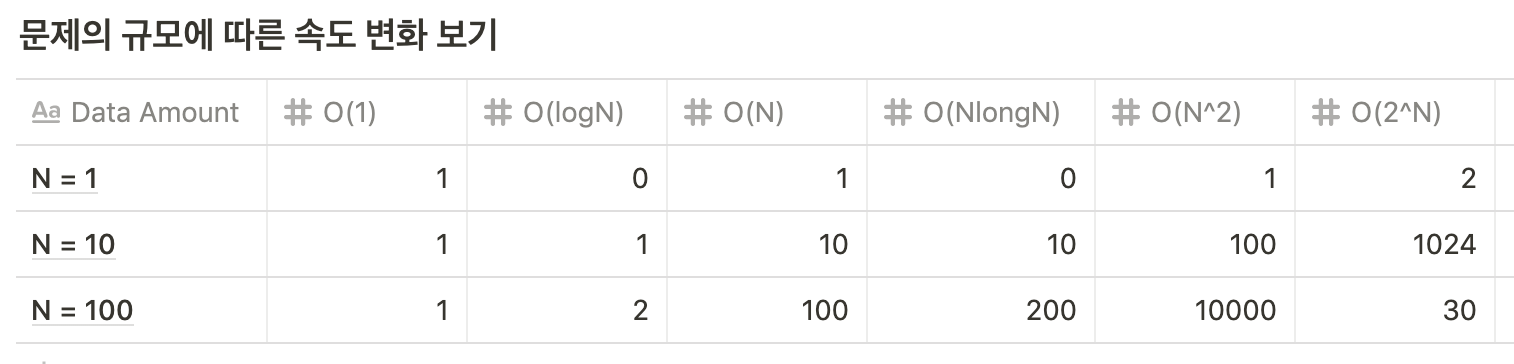
1. O(1) : constant time operation

- 데이터 개수와 상관없이 작업 시간이 일정
- ex) 배열에서 index 찾기, hash table에 데이터 추가

2. O(logN): logarithmic time operation

- 데이터 개수가 많을 수록 서서히 커브를 띄며 작업 시간 증가
- ex) binary search tree search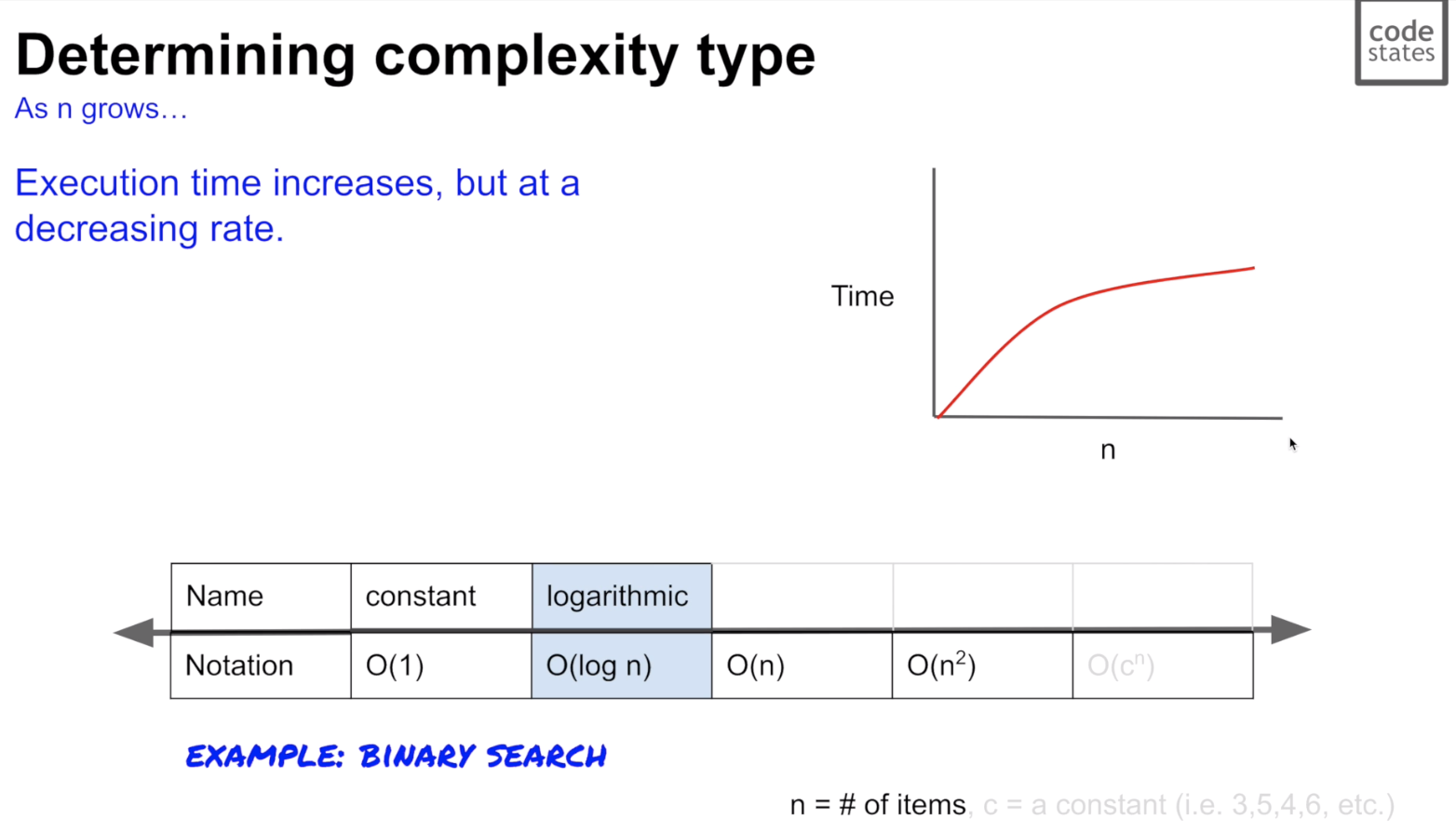

3. O(n): linear

- 개수와 작업시간은 정비례
- ex) linked list 혹은 배열에서 find

4. O(n^2): quadratic

- 일정 정도의 개수가 넘으면 작업 시간이 훨씬 늘어남
- ex) 이중 for문 구조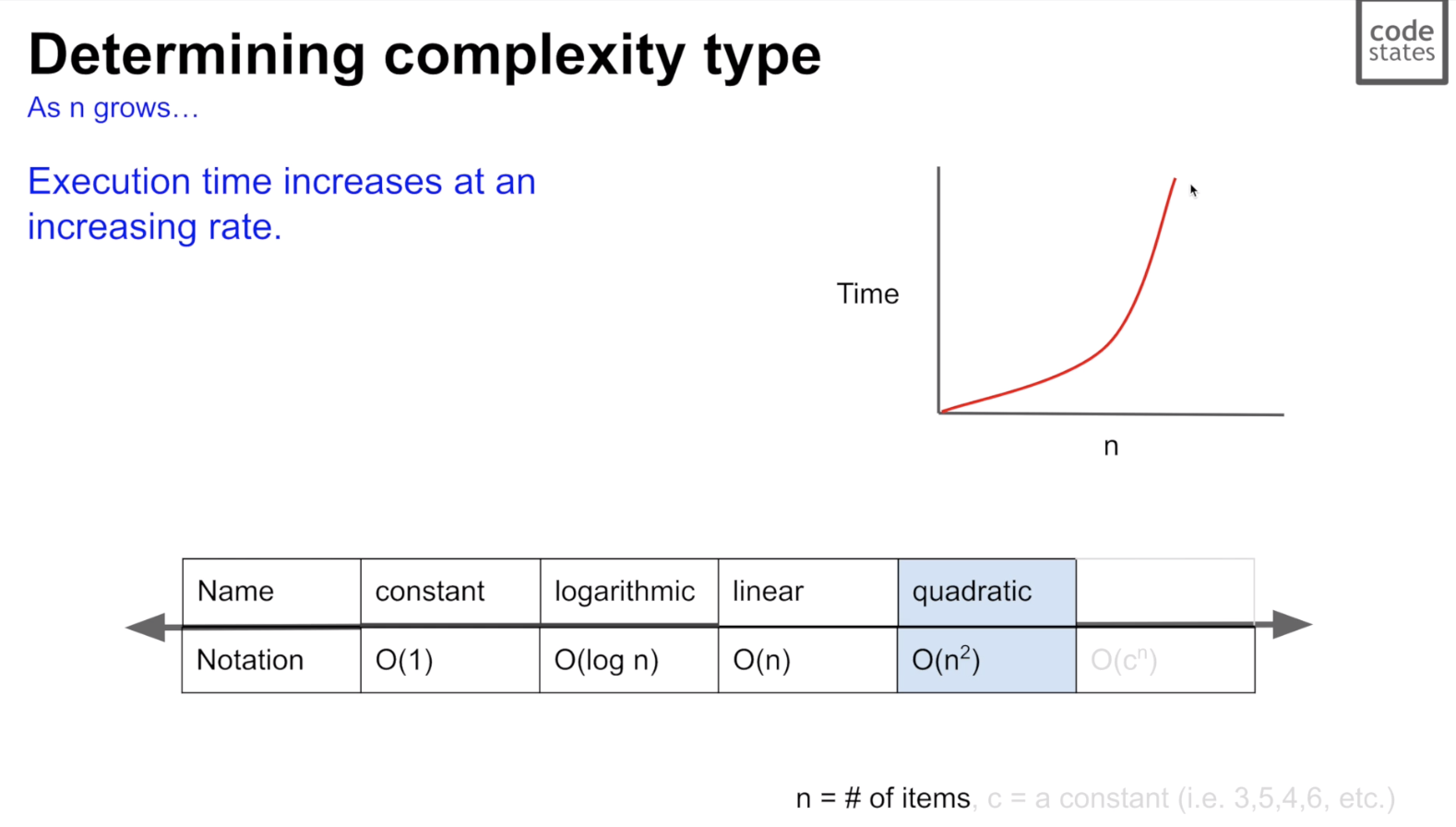

5. O(c^n): exponential

- 개수가 증가할수록 작업 시간이 급격히 늘어남
- ex) 피보나치 수열, recursion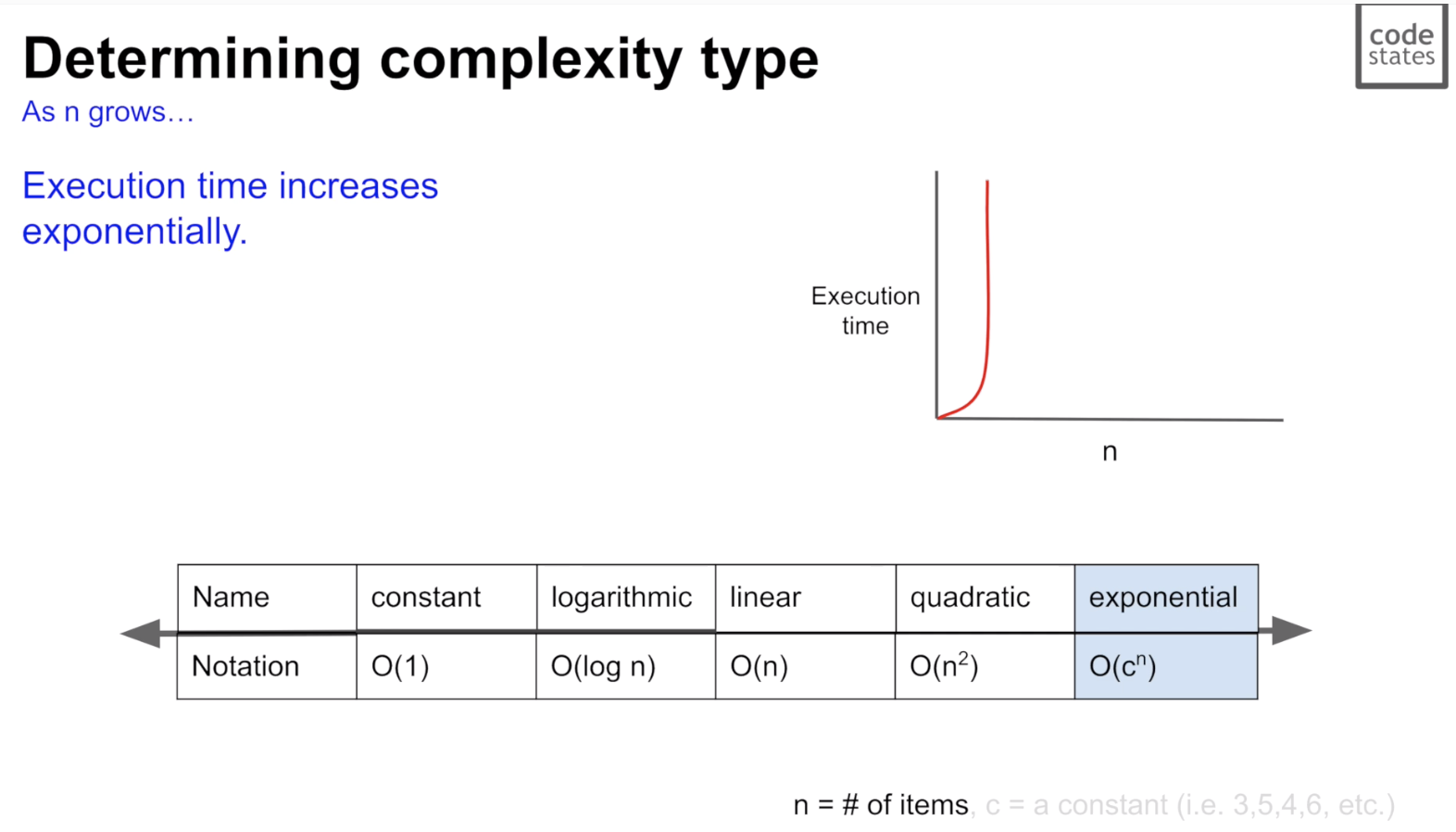

6. Big O Notation cheatsheet : https://www.bigocheatsheet.com/

3. Data Structure별 Big O 표기법

1. Array(자바스크립트의 배열 말고 일반적인 배열)

• 배열이란? 메모리 상에서 일정 부분 사이즈를 할당하고, 그 후 해당 공간에 데이터를 이어서(순서대로) 배치하는 자료 구조

• primitive data structure중 하나 → array를 사용해서 다른 데이터 구조 구현이 가능

• method별 Big O Notation
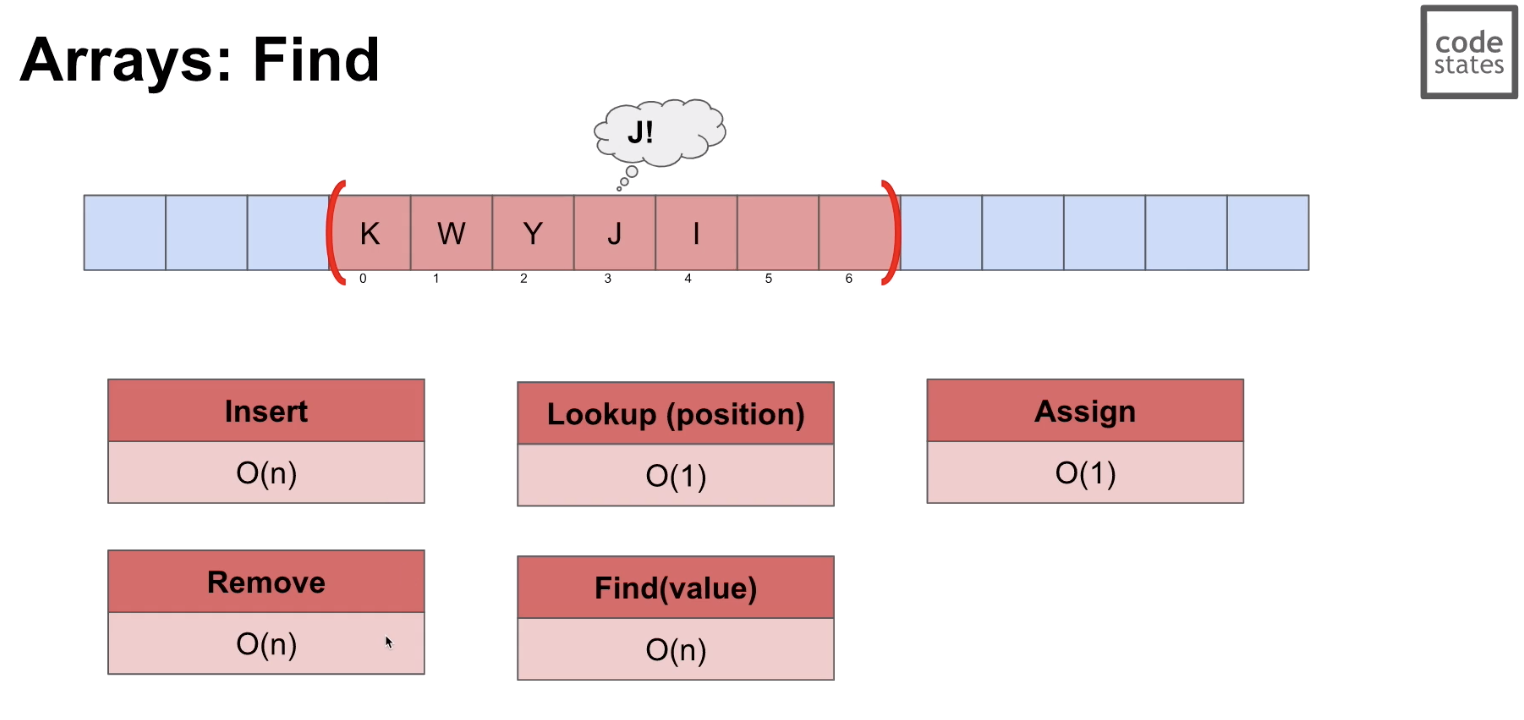
  - lookup position : O(1)
  - 특정 위치(인덱스)의 값을 찾는 기능
  - 배열은 순서대로 이어 붙어(contiguous) 있기 때문에 위치 파악이 가능하고, 바로 위치 확인 후 값을 불러올 수 있다. (head부터 임의의 위치를 검색할 필요가 없음)
  - assign: O(1)
  - 특정 위치에 data를 배치하는 것(override)
  - 위치 파악이 가능하기 때문에 바로 위치로 접근해 override 가능
  - insert: O(n)
  - 특정 위치에 data를 삽입하는 것
  - 삽입 시에는 그 뒤의 데이터들의 위치가 연달아 변경되기 때문에 최악의 경우 데이터들을 모두 옮겨야 할 수 있다.
  - remove: O(n)
  - 특정 위치의 data를 삭제하는 것
  - 삭제 시에는 그 뒤의 데이터들의 위치를 앞으로 당겨야 하기 때문에 최악의 경우 데이터들을 모두 옮겨야 할 수 있다.
  - find value: O(n)
  - 값의 특정 위치를 찾는 기능
  - lookup과 달리 인덱스를 활용해 데이터를 호출하지 않고 데이터들과 찾고자 하는 target과 비교를 계속해서 진행해야 한다.
  

2. Single Linked List

• unlike array, linked list는 메모리 상에서 순서대로 되어 있지 않고(non-contiguous) random 배치 되어 있다. 다음 노드를 기억하는 주소로 서로 연결되어 있다.

  • 따라서 위치나 data 검색을 위해서는 head를 꼭 알아야 한다.
    

  • find: O(n)

    • head부터 시작해서 원하는 값(target)이 나올 때까지 계속 데이터를 확인해야 한다.

  • lookup: O(n)

    • head부터 시작해서 찾고자 하는 값까지 계속해서 데이터를 확인해야 한다.

  • insert: O(1)

    • 넣고자 하는 위치에 바로 자신을 추가(이전/후 노드를 주소로 연결)하면서 1개 노드 안에서 처리

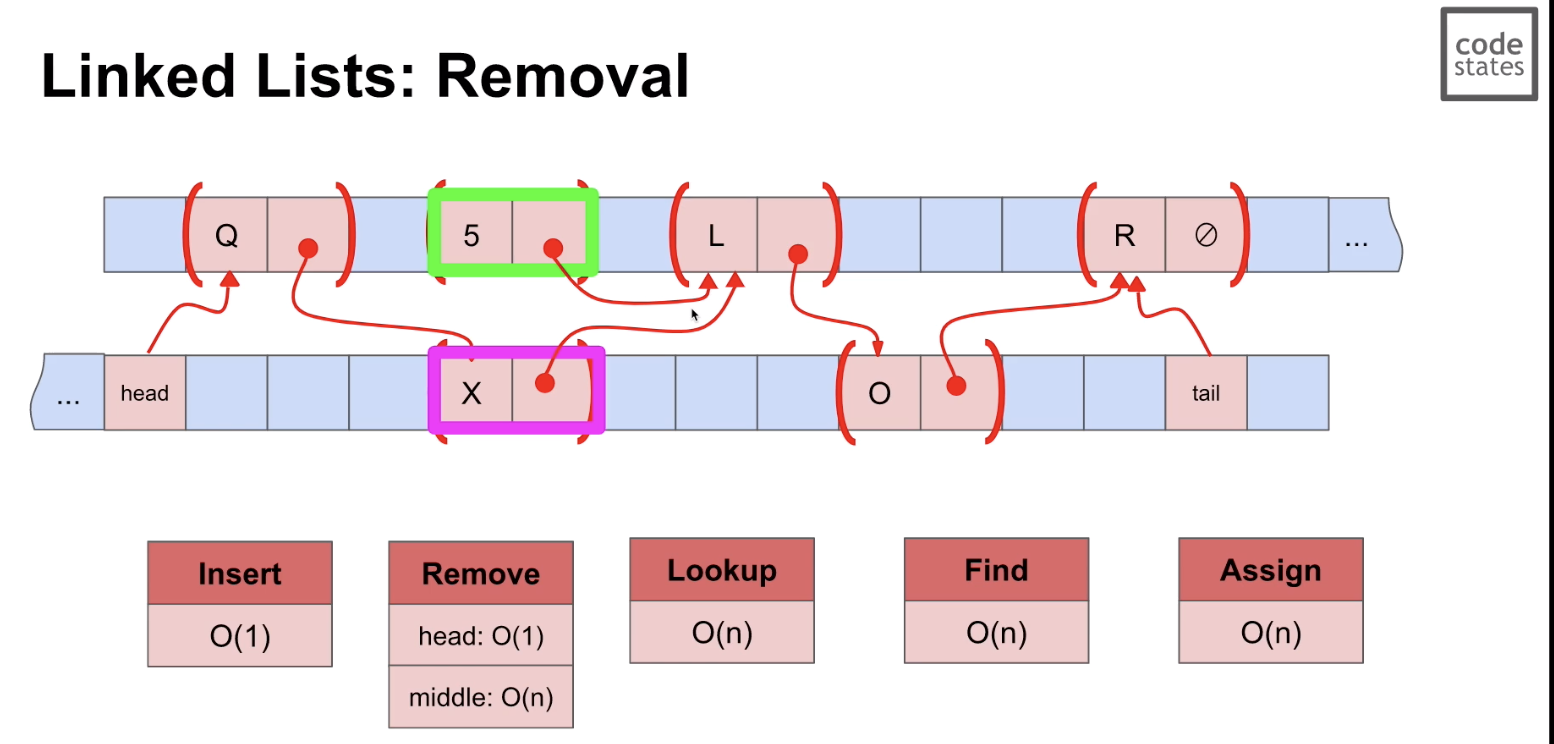
  • remove

    • 삭제할 값의 위치를 안다고 할 때 이전 노드의 주소를 자신의 다음 노드의 주소로 연결하고, 나를 지우면 된다.
    • 여기서 문제는 나의 위치를 먼저 알아야 한다는 것이다. 그 과정에서 이전 노드의 위치와 다음 노드의 위치 파악이 가능하다.
    • 중간 부분 삭제: O(n) - 내 전 노드가 무엇인지 모르기 때문 doubly linked list가 이 문제 해결
    • head 삭제: O(1) - 이전 노드와의 관계가 없기 때문에 바로 처리 가능

  • assign: O(n)

    • 원하는 위치에 값을 assign하기 위해서는 head에서 출발하여 원하는 위치까지 계속 데이터를 확인하며 진행한다.

3. Double Linked List

• Single Linked List와 달리 이전 값을 알려주는 값이 속성으로 존재한다.!
  

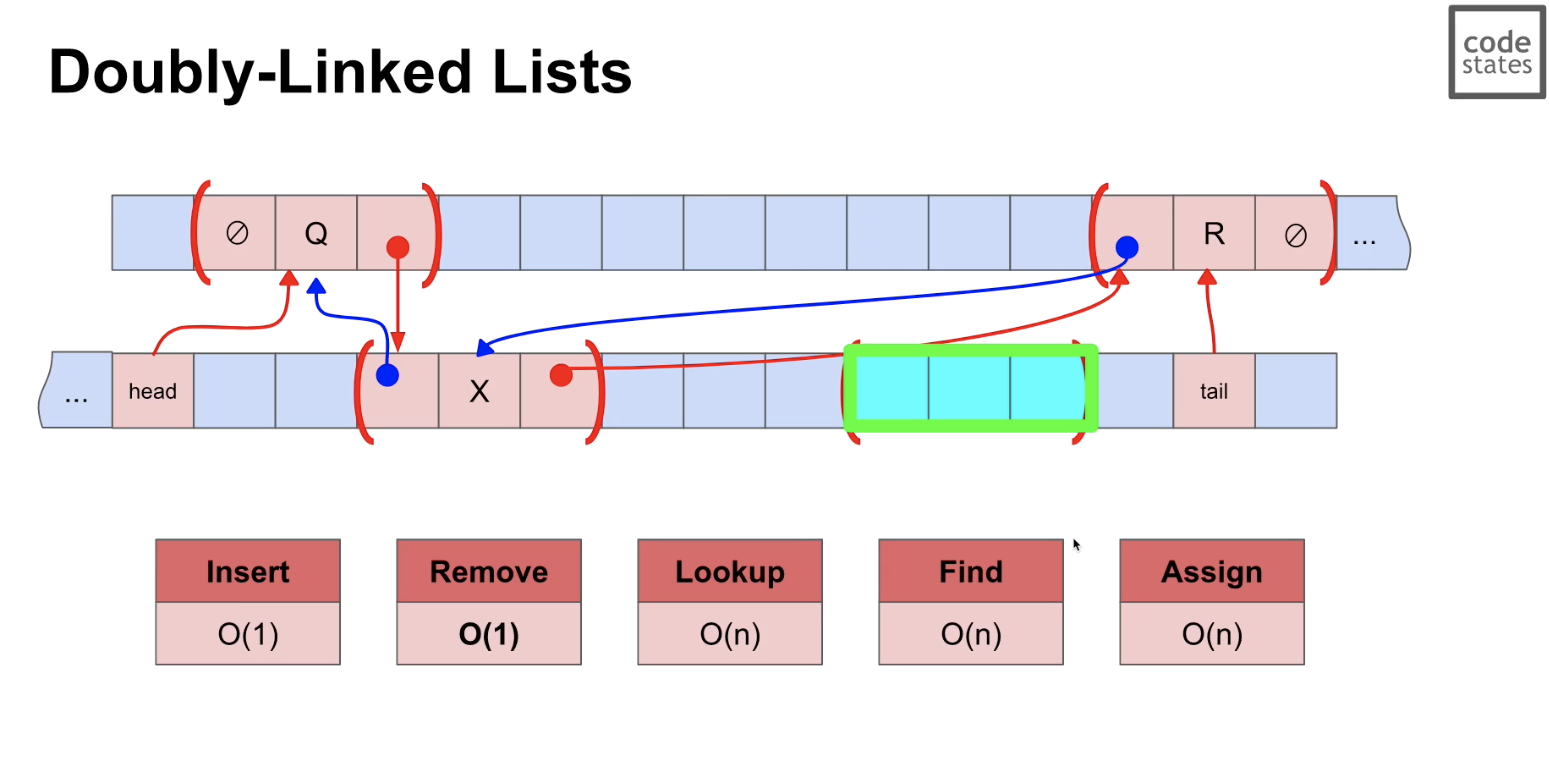
      - lookup: O(n)
      - find: O(n)
      - assign: O(n)
      - insert: O(1)
          - 앞/뒤/중간 등에 추가 가능하고, 추가하기를 원하는 위치를 아는 경우 O(1)
      - remove: O(1)
          - 나를 다음으로 기억하는 이전 값의 주소를 나의 다음 값으로 할당한다.
          - 그러면 나를 참조 해주는 link가 없어 지므로, garbage collector가 수집을 해 간다.
          - 처리가 끝나므로 1개의 동작으로 처리

4. Stack

• stack은 후입선출(LIFO) 구조로 하나의 데이터 공간에 데이터가 차곡 차곡 쌓이고, 제거할 때는 뒷데이터부터 제거하는 형태의 자료 구조이다.
  • method: push, pop, isEmpty, size 등
  • time complexity: 대부분 O(1)
    • push, pop, isEmpty, size method는 원하는 데이터 하나 안에서 작업이 이뤄진다.
    • access나 search method는 데이터를 계속해서 확인해야 하기 때문에 O(n)이 발생한다.

5. Queue

• queue는 선입선출(FIFO)구조로 하나의 데이터 공간에 데이터가 앞에서부터 쌓이고, 제거할 때에도 앞에서부터 제거되는 형태의 자료 구조이다.
• method: enqueue, dequeue, isEmpty, size 등
• time complexity: 대부분 O(1)
  • enqueue, dequeue, isEmpty method는 원하는 데이터 하나 안에서 작업이 이뤄진다.
  • size는 head와 tail의 비교를 할 때 O(n)
  • access나 search method는 데이터를 계속해서 확인해야 하기 때문에 O(n)이 발생한다. → Stack과 동일

6. Graph

• graph는 노드(버텍스)와 엣지(아크)로 구성되었고, 노드와 노드(버텍스와 버텍스) 사이를 엣지(아크)로 이어 상하위 개념이 없다. 비교적 자유로운 자료 구조이다.
  • method: insert(node, edge), remove(node, edge), find(hasNode, hasEdge), assign 등
  • time complexity:
    • search: DFS(위에서부터 가장 깊숙이 들어갔다가 다음 노드 레벨로 넘어가는 검색 방법), BFS(같은 노드 레벨을 수평적으로 모두 보고 그 하위 레벨로 이동하는 검색 방법)
    • time complexity
      • DFS - O(e): 엣지 개수
      • BFS - O(v): 버텍스(노드) 개수

7. Tree

• single linked list의 노드 구성이 자신의 값, 다음 노드의 주소 reference였다면
  trees 구조는 노드의 구성이 자신의 값, children reference다.
  • ex) DOM
    • find(DFS or BFS): O(n)
  • Binary tree
    • 트리 구조이나 노드가 최대 2개씩 가지는 특정한 규칙을 가지고 있음
    • 이진트리, 포화이진트리, 완전이진트리, 편향이진트리 등 종류가 다양
    • search/find
      • average - O(log N)
      • worst - O(n)
      • 편향이진트리의 경우에는 time complexity가 O(n)까지 갈 수 있기 때문에 이럴 때에는 할당 순간부터 rebalancing(오른쪽, 왼쪽 값의 depth가 2이상이 되는 경우 노드의 위치를 적절히 변경해줌)을 통해서 이진탐색트리가 가진 장점인 O(logN)을 놓치지 않게 할 수 있다.

8. Binary Search Tree

• Binary Trees: 정렬이 되어 있다면 tree 구조에서도 array를 사용하지 않고도 binary search가 가능하다.
  • Q. 배열의 형태로도 정렬하여 검색에 사용할 수 있지 않나?
    → A. 배열은 continuous block으로 공간이 차지되어 있다.
    반면에 binary search tree 구조는 linked list 등을 사용해서 continous block을 차지하지 않기 때문에 메모리 효율성이 더 높은 편이다.
  • binary search tree의 평균적 time complexity: O(logN)

9. Hash Table

• hash table은 데이터를 받아 hash function을 적용해 hash key를 index로 가지는 공간에 할당하는 자료 구조이다.
  • method: insert, remove, retrieve, resize, each 등
  • hash table에서 데이터 탐색이나 삽입/삭제 등은 hash function으로 받은 index를 기준으로 별도의 추가 절차 없이 바로 처리가 되기 때문에 O(1)다.
  • 그러나 limit이 75%를 넘거나 25%보다 작아져 테이블의 리사이징이 필요한 경우에는, 조정된 테이블에 새로이 값을 부여하는 과정에서 O(n)의 시간복잡도를 보인다.
  • 또 가끔 hash function에 의해 나온 index가 계속해서 같은 bucket을 가리킨다면 이 또한 O(n)의 복잡도를 가지게 되기 때문에 hash function이 다양한 index 값을 output으로 나오게끔 함수 구성을 해야 한다.