Hopfield Network is all you need 살펴보기

nawnoes·2021년 1월 12일
Deep Learninghopfield network
0

NLP

목록 보기
23/45

Hopfield Network is all you need 살펴보기

최근 트랜스포머를 사용하다 보니 모델의 크기나 몇가지 제한 사항들을 느끼면서 새로운 모델들을 보고 다른 가능성들이 있는지 살펴보고 싶었습니다.

이번 글을 참조한 블로그들을 정리하여 전통적인 홉필드 네트워크부터 현대의 홉필드 네트워크까지 살펴봅니다.

1. 전통적인 홉필드 네트워크

홉필드 네트워크는 물리학적인 스핀 모델에서 착안하였으며, 에너지 개념을 신경망에 처음으로 도입하였습니다.

홉필드 네트워크의 제한사항
① 뉴런 사이의 weight는 대칭이다 wij=wjiw_{ij} = w_{ji}
② 각 뉴런들은 완전히 비동기적으로 동작할 때만 안정된 상태에 도달 가능.

첫번째 제한 사항은 생물학적인 뉴런에서 일반적으로 대칭성이 성립할 수 없기 때문에 중대한 제약사항으로 볼수 있습니다. 두번째 제한 사항의 경우 비동기 적인 경우에만 동작하는것을 가정하므로 동기적으로 작동할 때에는 에너지가 안정적인 상태에 도달하지 못할 수 있으며 루프에 걸릴 가능성도 있습니다.

아이디어 및 구조

뉴런의 작용을 단지 임계값을 작용으로 보고 훈련에 의한 정보가 연결강도에 의해 표현된다는 이론에 기초한다. 연상기억(associative memory)나 순회판매원 문제(Traveling Saleman Problem)과 같은 최적화 문제를 해결하는데 유용하며, 많은 수의 비동기적이고 국소적인 계산을 통해 전역최적화를 이룰 수 있다는것이 증명되어 많은 관심을 끌었습니다.

홉필드 네트워크는 기존 신경망과 다르게 고정된 가중치를 이용하여 완전한 정보를 연상하는 차이점을 가집니다. 홉필드 네트워크는 학습 패턴에 대해 계산된 고정 가중치 행렬을 저장하고, 입력값이 들어 올때마다 가중치 행렬을 이용해 입력값과 유사한 학습 패턴을 연결합니다.

또한 홉필드 네트워크는 모든 뉴런이 양방향으로 연결된 신경회로망의 동작 모델로서 양극화된 입력을 받아, 양,음의 에너지상태를 출력합니다.


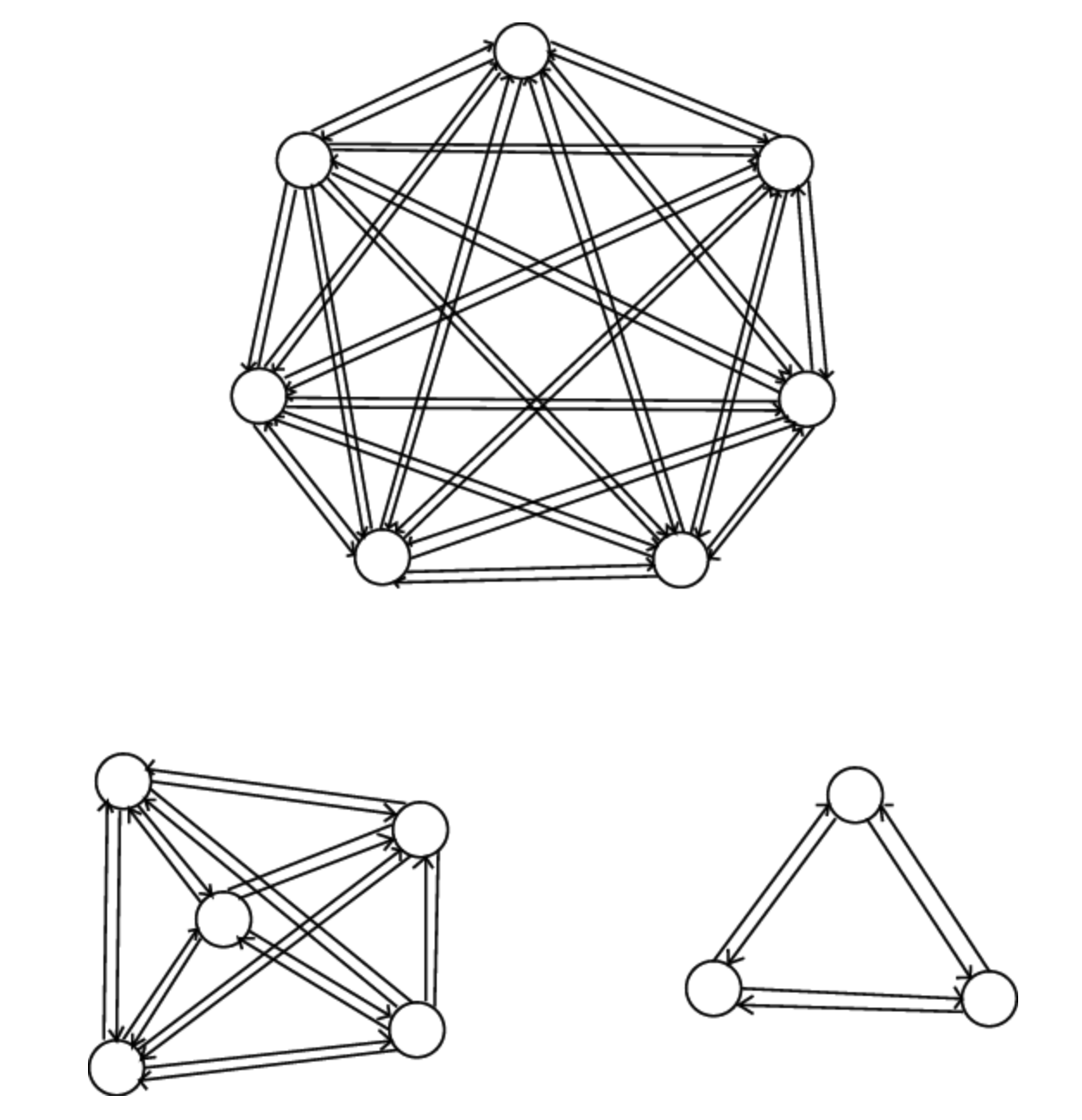
홉필드 네트워크는 완전연결된 구조로 되어 각 유닛은 다른 모든 유닛들과 직접적인 연결 경로를 가집니다. 그리고 각각의 경로들은 연결에 대한 가중치를 가지고 있습니다.

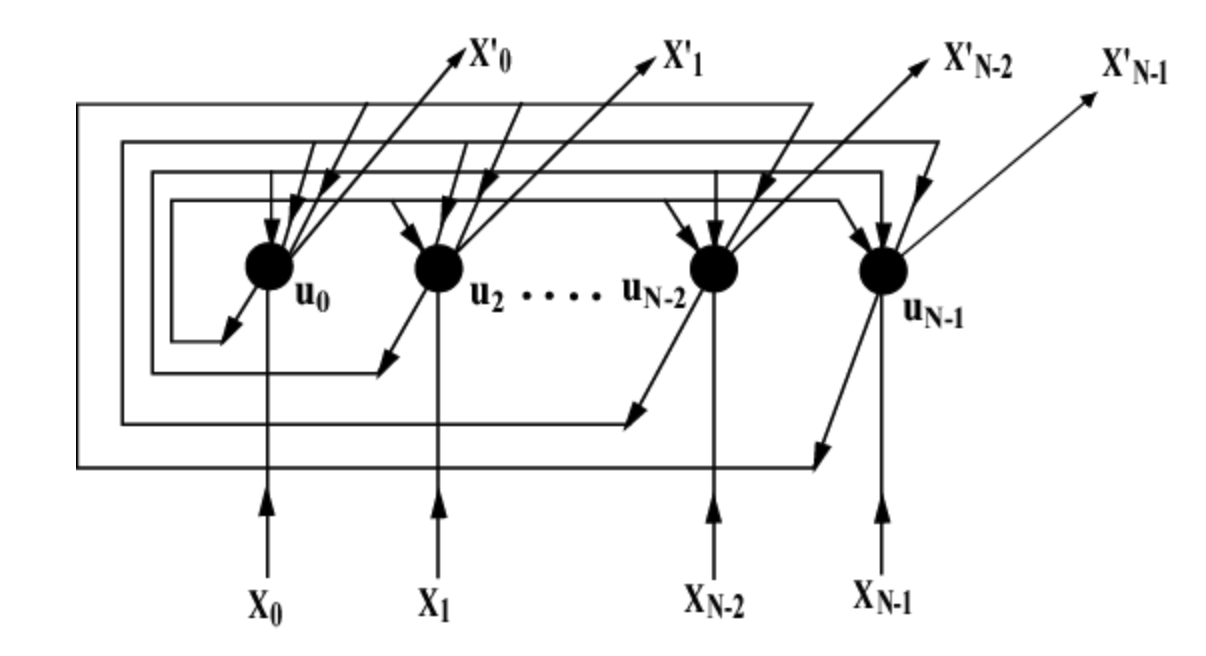
홉필드 네트워크의 연상 기억장치(associative memory)

홉필드 네트워크는 연상 기억장치로 효과적으로 동작합니다. 여기서 말하는 연상기억장치란 일반적인 컴퓨터에서 내용 주소화 기억장치로써 기억장치에 저장된 데이터에 접근하기 위해 주소를 사용하는 것이 아닌, 기억된 데이터의 일부분을 이용해 원하는 정보의 위치를 얻어, 그위치에서 데이터에 접근하는 기억장치의 역할을 말합니다.

인간과 비교 하자면 인간의 과거의 경험했던 것들을 새로운 경험들과 연관, 통합함으롰서 새로운 개념을 창조해내는 능력을 가지고 있습니다. 이와 같이 홉필드 네트워크에서도 심한 노이즈나 불완전한 패턴, 왜곡된 패턴이 입력으로 들어왔을때, 기존에 학습한 패턴을 바탕으로 본래의 완전한 형태를 유추할 수 있습니다.

홉필드 네트워크 알고리즘

① 학습 패턴에 대한 양극화(Polar) 연산을 적용
② 학습 패턴에 대한 홉필드 네트워크의 가중치 행렬을 계산
③ 계산되니 가중치 행렬을 저장
④ 입력 값이 들어오면 위에 저장된 가중치 행렬을 이용해 입력 값에 대한 학습 패턴을 연상

설명

가장 단순한 연상 메모리는 NN 패턴들 {xi}iN\{x_i\}^N_i의 외적의 합과 같습니다. NN 패턴 {xi}iN\{x_i\}^N_i들은 우리가 저장하길 원하는 패턴입니다.(Hebbian learning rule에 따라서). 전통적인 홉필드 네트워크에서는 패턴들이 양극성(polar)를 가지며 xi∈{−1,1}dx_i\in\{-1,1\}^d와 같으며 이때 dd는 그 패턴들의 길이를 의미합니다. 이때 웨이트 매트릭스(weight matrix) WW는 아래와 같습니다.

W=∑NixixiTW= \underset{i}{\overset{N}{\sum}} x_ix^T_i

웨이트 매트릭스 WW는 저장된 패턴들을 의미하며, 이 패턴들은 상태 패턴(state pattern) ξ\xi에서 찾을 수있는 패턴을 말합니다.

표기법 Notation

  • NN 저장된 패턴(stored pattern): {xi}iN\{x_i\}^N_i
  • 상태패턴(state pattern)또는 상태(state): ξ\xi

동기 업데이트(Synchronous Update Rule) 은 상태패턴 ξ\xi를 웨이트 매트릭스 WW와 반복적으로 곱하고 bias를 뺀 후 sign 을 취한다.

이때의 sign이 어떤 의미인지 확인 필요.

ξt+1=sgn(Wξt−b)...(2)\xi^{t+1} = sgn(W\xi^t - b) ... (2)

이때 b∈Rdb \in \mathbb{R}^d인 bias 벡터이다. 이 벡터는 모든 컴포넌트에 대한 임계값으로 해석될 수 있습니다.

비동기 업데이트(Asynchronous Update Rule) 은 ξ\xi 의 한 컴포넌트에 대해 업데이트를 수행하며, 그후에 업데이트를 위해 다음 컴포넌트를 선택합니다. 만약 ξt+1=ξt\xi^{t+1}=\xi^t라면 수렴합니다.
방정식 (2)의 업데이트 룰에 대해 비동기적인 방식은 에너지 함수(energy function) EE를 최소화 하는것입니다:

E=−12ξTWξ+ξTb=−12∑di=1∑dj=1wijξiξj+∑di=1biξiE = -\frac{1}{2}\xi^TW\xi + \xi^Tb = -\frac{1}{2} \underset{i=1}{\overset{d}{\sum}} \underset{j=1}{\overset{d}{\sum}} w_{ij}\xi_i\xi_j + \underset{i=1}{\overset{d}{\sum}}b_i\xi_i

이전 논문들에서 보여주듯이, 수렴 속성들은 웨이트 매트릭스 WW의 구조와 노드들이 업데이트 되는 방법들에 결정:

  • wii≥0w_{ii} \ge 0와 wij=wjiw_{ij}=w_{ji}인 비동기 업데이트에 대해, 안정상태(stable state)로 수렴되어 업데이트
  • wij=wjiw_{ij} = w_{ji}인 동기 업데이트에 대해, 안정상태나 길이 2의 제한된 사이클로 수렴

비동기업데이트 규칙과 대칭웨이트들(symmetric weights)에 대해서 E(ξt+1)≤E(ξt)E(\xi^{t+1}) \le E(\xi^t)는 유지되고, ξt\xi^t의 모든 컴포넌트에 대해 업데이트가 E(ξt+1)=E(ξt)E(\xi^{t+1}) = E(\xi^t) 인 경우에는 EE에서 지역 최소값에 도달할 수 있습니다. 모든 저장된 패턴인 {xi}iN\{x_i\}^N_i는 홉필드 네트워크에서 고정된 포인트여야 합니다. 즉, xi=sgn(Wxi−b)x_i = sgn(Wx_i-b) 는 E의 지역 최소값이어야 합니다.

Hopfield network 예제

아래 예제를 통해 홉필드 네트워크의 예제를 살펴보고자 합니다. 아래 설명하는 예제에서는 바이어스가 없는 벡터가 사용되었습니다. 바이어스가 없는 벡터가 사용되었다는것의 의미는 역 이미지를 취할때 같은 에너지를 가지는 것을 의미한다고 합니다.(This means that taking the inverse image, i.e. flipping all pixels at once, results in the same energy.)

정확하게 어떤 의미인지는 잘 이해가 가지 않습니다.

한개의 Input인 경우

먼저 아래의 입력 이미지를 저장한 다음에 패턴을 추출해야합니다.

연상 메모리의 경우 양극성 상태와 패턴들을 가지기 때문에 위의 이미지를 아래와 같이 흑백의 이미지로 변환합니다.

위와 같을 때 웨이트 매트릭스 WW의 경우 흑백 이미지인 xhomerx_{homer}의 외적(outer product)한 값과 같습니다.

W=xhomerxhomerT,xhomer∈{−1,1}dW= x_{homer}x_{homer}^T, x_{homer} \in \{-1,1\}^d

이때의 dd=64x64를 의미합니다.

예제 이미지에서 절반을 마스킹하는 경우에도 위의 원본 이미지를 복구 할 수 있을까요?

위의 마스킹한 이미지를 초기상태(initail state) ξ\xi로 하고, 웨이트 매트릭스 WW를 곱연산을 통해 업데이트를 하며, 이 업데이트는 원본의 이미지가 복구될때까지 반복해서 업데이트 합니다.

Input이 3개인 경우

위의 예에서는 Input이 한개인 경우를 살펴보았습니다. 입력이 3개가 되는 경우 웨이트 매트릭스 WW 는 저장된 3개의 패턴의 외적 합으로 만들어집니다.

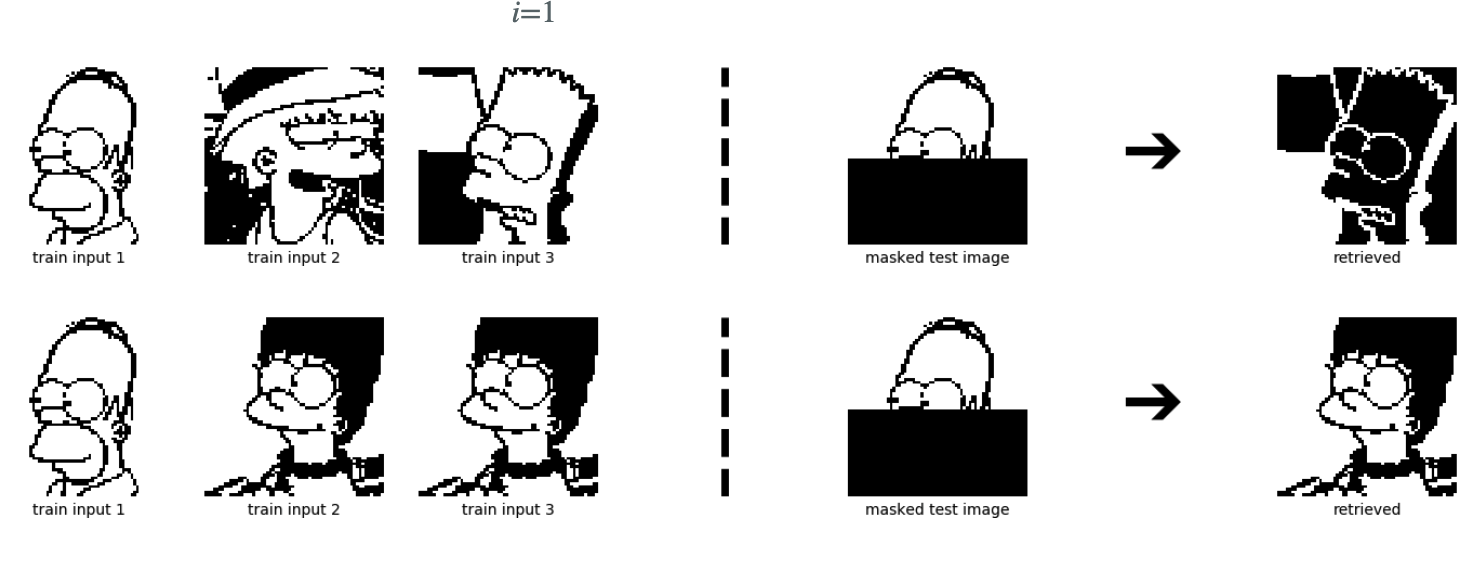
W=∑di=1xixiT,xi∈{−1,1}dW= \underset{i=1}{\overset{d}{\sum}} x_ix_i^T, x_i \in \{-1,1\}^d


위 그림에서 좌측은 입력에 따라 저장된 3개의 패턴입니다. 우측 부분은 마스킹된 패턴 ξ\xi와 추출된 패턴 ξnew\xi^{new}입니다.

그림에서 위쪽 부분 추출된 결과가 호머가 아닌 바트가 나와 불완전하게 보이기도 하지만 흥미로운 2가지 부분이 있습니다.
① 마스킹된 원본 이미지는 -1 값을 가진 픽셀이 많아졌기 때문에 \<xmaskedhomer,xbart \<x_{masked homer}, x_{bart} \>의 외적이 \<xmaskedhomer,xhomer \<x_{masked homer}, x_{homer} \>보다 더 큰 이상한 결과가 나오게 되었다.
② 위에 언급한 것과 같이 만약 바이어스가 없는 벡터가 사용된다면, 패턴의 역(모든 픽셀이 한번에 뒤집히는것)은 동일한 에너지를 가진다.

따라서 위의 예제는 부정확해보이지만, 위의 2가지 이유로 사실상 정확한것과 같습니다. 그러나 이미지의 하단의 예제에서는 추출된 결과가 부정확한데 그 이유는 2∗xmarge2*x_{marge}의 웨이트가 xhomerx_{homer}의 웨이트를 단순하게 덮어 썼기 때문입니다. 위 두 예제는 모두 첫번째 업데이트 스텝을 거친후에 추출된 결과입니다. 그러나 그 결과는 업데이트 스텝을 조금 더 진행하여도 변하지 않습니다.

Input이 6개인 경우

아래의 그림은 6개의 패턴에 대해 결과를 추출한 그림입니다.

결과를 보면 잘못된 결과가 출력된것이 분명합니다. 누군가는 이러한 잘못된 결과가 나온것을 홉필드 네트워크의 제한된 스토리지 용량(limeted storage capacities)때문으로 추측할 수 있지만 제한된 스토리지의 용량은 직접적인 원인이 아님을 아래에 보입니다.

  • 에러에서 자유로운 추출된 패턴에 대한 스토리지 용량 CC:

    C≅d2log(d)C \cong \frac{d}{2log(d)}

    이때 dd는 입력의 차원을 나타냅니다.

  • 작은 에러를 가지는 스토리지 용량 CC:

    C≅0.14dC \cong 0.14d

    와 같습니다. 이때, 용량을 직접 계산해보면 C≅0.14d=0.14∗64∗64 570C \cong 0.14d = 0.14 * 64* 64 ~ 570으로 불충분한 스토리지에 대한 부분은 직접적인 원인이 아님을 알수 있습니다. 게다가 예의 패턴들은 상관관계를 가지므로 추출된 결과가 에러를 가지게 됩니다.

결과적으로 상관관계가 밀접한 가까운 패턴들을 구별하고 분리할 수 있는 모델을 필요로합니다.

진행중...

References

profile
nawnoes
이전 포스트

데이터전처리 - 나무위키 덤프 텍스트 데이터 얻기

0개의 댓글