Performer - RETHINKING ATTENTION WITH PERFORMERS

nawnoes·2021년 1월 29일

NLP

목록 보기

25/45

RETHINKING ATTENTION WITH PERFORMERS

Perforemr 논문에 대해 간략하게 살펴보고자 합니다. performer는 기존의 트랜스포머가 self-attention 계산시에 제곱의 시간 및 공간 복잡도를 가지는 것을 선형으로 변형하여 트랜스포머의 소프트맥스 어텐션에 근사하는 방법을 제안하였고 그 모델의 이름이 Performer 입니다.. Performer에서는 FAVOR+(Fast Attention Via positive Orthogoanl Random feature approach) 를 사용하였습니다. FAVOR+는 softmax를 커널화 가능한 어텐션으로 효율적으로 모델링 하는데 사용할 수 있다고 합니다.

Performer는 기존의 트랜스포머와 양립할수 있으며 이론적으로 보장되며, 강력한 구조를 가집니다.

트랜스포머는 기존에 강력한 성능을 보여 많은 곳에 사용되었고, 그 이후 여러 모델들이 제안되면서 트랜스포머가 가진 문제들을 개선하기 위한 많은 시도들이 있었습니다. 하지만 트래스포머는 모델에 사용하는 최대 토큰의 개수에 따라 많은 복잡도를 가지게 됩니다. 예를들어 512 토큰을 사용하는 트랜스포머 모델의 경우 어텐션 계산시에 512*512 의 복잡도를 가지게 됩니다. 하지만 이러한 복잡도는 더 많은 토큰을 고려한 어텐션을 사용하고 싶은 경우 많은 비용이 들게 됩니다.

위와 같은 문제들을 해결하기 위해 다양한 시도들이 있었지만 트랜스포머만큼의 성능을 보장하는데 부족함이 있었습니다. 그 외에도 학습과정에서 activation을 위해 저장하는 것을reversivle residual network을 통해 줄이는 테크닉과 어텐션의 웨이트들을 공유하는 방법들도 있었습니다. 하지만 이러한 방법들은 어텐션에 대한 충분한 근사가 부족한 부분에서 긴 시퀀스 문제를 해결하는것을 늦췄을지도 모릅니다.

이러한 문제들을 해결하고자 저자들은 Performer를 제안 하였고, Performer는
full-rank attention에 대해 정확하고 실질적으로 평가할 수 있는 모델이지만 선형적인 시간 및 공간 복잡도를 가지며, sparsity나 low-rankness등과 같은 어떠한 것에도 의존하지 않습니다. Performer는 FAVOR+를 이용합니다. FAVOR+는 저자들이 제안하는 가우시안 커널과 소프트맥스를 근사하기 위한 새로운 메소드입니다. 결과적으로 Performer는 커널을 이용해 기존의 트랜스포머와 함께 사용 가능한 선형구조로 강력한 이론적인 보증을 해주는 모델이기도 합니다.

FAVOR+는 소프트맥스를 넘어 다른 커널화 가능한 어텐션 메커니즘을 효율적으로 모델링하는 것에 적용할 수 있습니다. FAVOR+의 표현력은 처음으로 대규모 스캐일의 태스크들에 대해 다른 커널들과 소프트맥스를 정확하게 비교하고 최적의 어텐션-커널들을 찾는데 중요한 역할을 합니다. FAVOR+는 기존의 어텐션을 확장 가능한 대체방법으로써 트랜스포머를 넘어 다양한 분야에 적용될 수 있습니다. 적용 가능한 분야로는 컴퓨터비전, 강화학습, 소프트맥스 크로스엔트로피 로스를 이용한 학습, Combinatorial 옵티마이제이션과 같은 다양한 곳에 적용될 수 있습니다.

FAVOR+는 reversivle layer와 cluster-based attention등과도 결합될수도 있습니다.

2. FAVOR+ 동작 원리와 Positive Orthogonal Random Feature

Performer에 사용하는 FAVOR+ Attention의 원리를 학습해보고자 합니다.

Kernel Trick

What is the kernel trick? Why is it important? 참고

낮은 차원에서 분류를 하기 어려운 문제의 경우 더 높은 차원으로 매핑하여 분류를 하는 방법이 있습니다. 하지만 차원이 높아 질수록 space와 computation 비용이 높아 지기 때문에 이러한 경우 커널 트릭을 사용해 문제를 해결합니다.

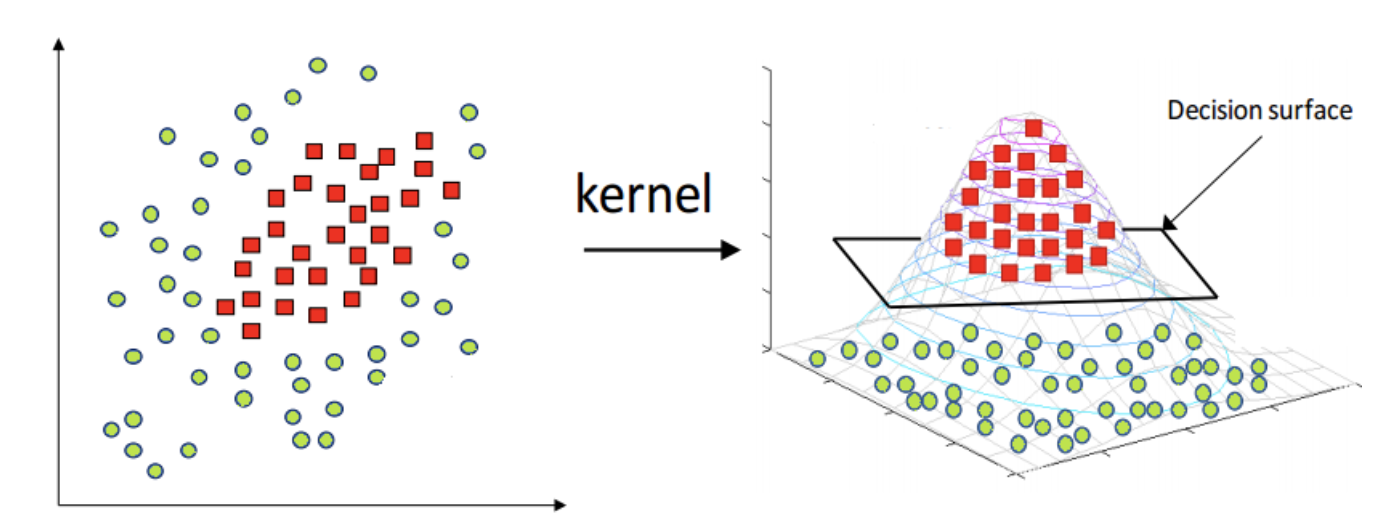
커널트릭은 위와 같이 더 높은 차원의 공간에서 데이터의 좌표를 계산하지 않고 original feature space에서 계산 할 수 있도록 합니다. 따라서 커널트릭은 높은 차원으로 데이터를 변환하지 않으면서도 효율적인 방법으로 계산 할 수 있는 장점이 있습니다. 예전에는 SVM에서 주로 사용 되었지만 커널 트릭은 dot products(x,y)가 사용되는 어디에서든지 사용할수 있다고 하며, 이러한 이유에서 Performer에서 Scaled Dot-Product Attention에 커널 트릭을 이용한 것으로 생각됩니다.

대표적인 커널 함수들

대표적으로 많이 사용되는 커널로는 polynomial kernel과 RBF(Radial Basis Function) kernel 이 있습니다.

polynomial kernel

polynomial kernel은 유사성 뿐만 아니라 입력의 샘플들의 feature들의 조합을 이용한다고 볼 수 있다. n개의 origin feature와 d개의 degrees of polynomial을 이용해 $n^d$ 으로 확장된 feature를 가진 polynomial kernel을 가집니다.

K(x,y) = (x^Ty+1)^d

RBF(Radial Basis Function) kernel

RBF kernel은 Gaussian kernel로 불립니다. RBF는 테일러 급수에 따라서 확장 될 수 있기 때문에 feature space에서 제한된 차원을 가집니다. $\gamma$ 파라미터의 경우 얼마나 single training example에 많은 영향을 미치는지 결정하는 파라미터입니다. 감마 파라미터의 값이 크면 클 수록 다른 example들에 미치는 영향력이 커지게 됩니다.

k(x,y) = e^{-\gamma||x-y||^2} ,\gamma >0

테일러급수

테일러급수(Tayler Series)는 어떤 미지의 함수 $f(x)$ 을 아래 식과 같이 근사 다항함수로 표현하는 것을 말합니다. x=a 근처에서만 성립하며, x가 a에서 멀어지면 큰 오차를 갖게되며, 근사 다항식은 차수가 높을 수록 $f(x)$ 를 보다 잘 근사하게 됩니다.

f(x) = p_{\infty}(x)

p_n(x) = \sum_{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a)^k

테일러 급수가 사용되는 용도로는 사라밍 다루기 어려운 복잡한 함수들을 쉬운 다항함수로 대체할 수 있습니다. 이렇게 바뀐 다항함수를 통해 함수의 특성을 분석하기에 보다 편리해지고, 모델을 단순화 할 수 있기 때문에 커널에서 사용한것으로 보입니다.

Random Features

In Random Features for Large-Scale Kernel Machines 논문에서는 random feature map $z$ 를 통해 $K$ 에 근사했습니다. $z: R^L \mapsto R^R$ 으로, random feature map을 통해 커널을 근사할 수 있습니다.

K(x_i,x_j) = \varphi(x_i)^T \varphi(x_j)

커널을 Random Feature map을 통해 근사합니다.

\varphi(x_i)^T \varphi(x_j) \approx z(x_i)^Tz(x_j)

위 논문에서는 가우시안 커널(RBF 커널)에 대해 푸리에 변환을 이용한 $z$ 의 샘플링을 통해 커널에 근사 할수 있음을 보였습니다. 가우시안 커널은 다음과 같으며, $K_{gaussian}(x_i,x_j) = exp(-\gamma||x_i-x_j||^2)$ 이를 근사하기 위한 Random Feature는 아래와 같습니다
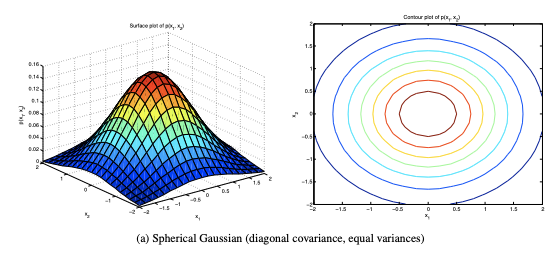
$\omega \sim \mathcal{N}_R(0,I)$ 은 spherical Gaussian에서 샘플링 됩니다.

Spherical Gaussian이란
확률 분포가 구면(원형) 대칭이므로 이를 구면 가우시안(Spherical Gaussian)

참고 문서

z_{\omega}(x) = \begin{bmatrix} cos(\omega^Tx) \\ sin(\omega^Tx) \end{bmatrix}

위와 같은 방법을 통해 dot-prouct 연산을 $R^L$ 에서 하지않고 $R^R$ 에서 수행할 수 있습니다. 일반적으로 $R\ll L$ 이기 때문에 성능에서 많은 이점을 가지고, Random Fourier Feature를 통해 커널 $K$ 를 가우시안 커널 $K_{gaussian}$ 으로 근사 할수 있는것을 확인할 수 있습니다.

Attention

위에서는 커널을 통해 dot-product 연산을 커널로 바꾸어 연산하는 것을 보았고, Random Feature Map을 통해 커널을 근사하는 방법을 보았습니다.

Performer에서는 트랜스포머에서 어텐션 연산시에 Dot-Product 연산을 Softmax Kernel을 통해 근사하였고, 이때의 소프트맥스 커널은 앞에서 보인 가우시안 커널을 통해 정리 될수 있음을 보입니다. 앞 장에서 가우시안 커널의 경우 Random Feature Map $z$ 를 통해 근사할 수 있음을 보였습니다.

아래에서는 Random Feature map을 통해 Performer에서 사용하는 FAVOR+ Attention을 보고자 합니다.

작성중...