BigBird, Block Sparse Attention

nawnoes·2021년 8월 2일

NLP bigbird block sparse attention sparse attention

NLP

목록 보기

31/45

보다 큰 모델을 학습하기위해 full self-attention이 아닌 sparse self-attention에 대해 학습해보고자 한다. huggingface blog bigbird 글을 읽으면서 정리. 보다 자세하고 정확한 내용은 앞의 블로그를 참고.

Introduction

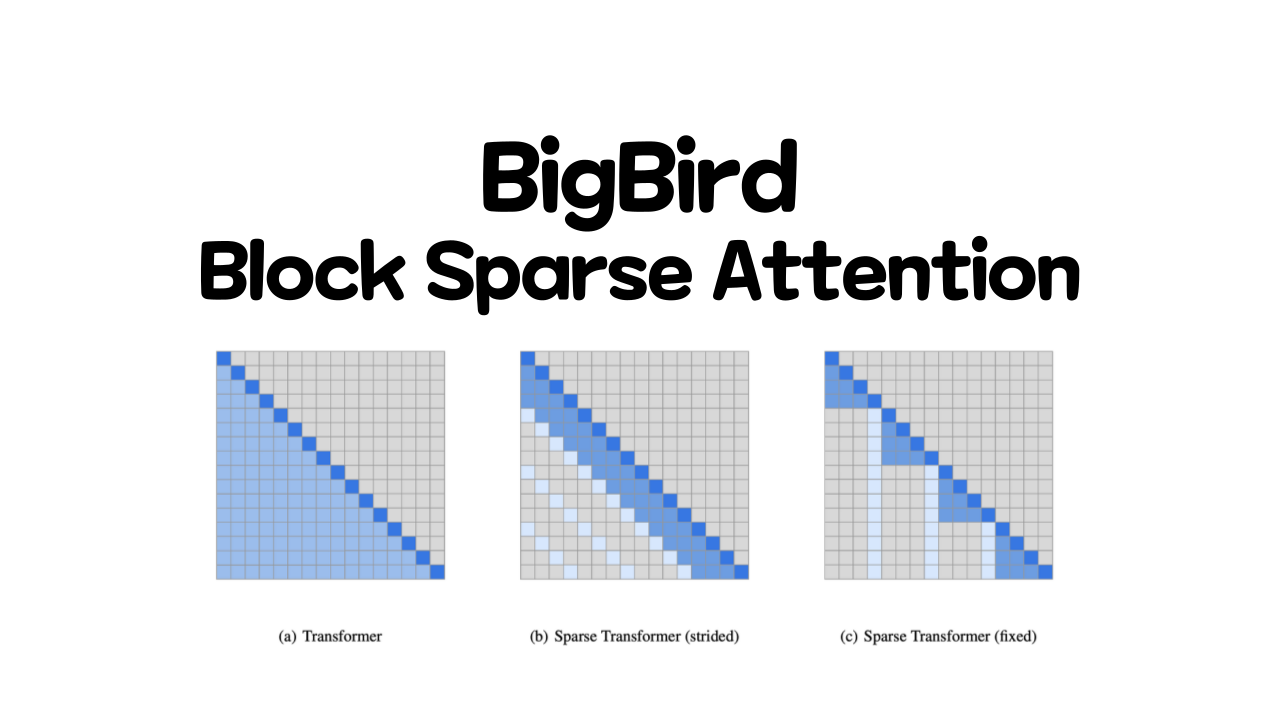
NLP분야에서 트랜스포머 모델의 사용은 갈수록 증가하지만 트랜스포머 모델은 $O(n^2)$ 의 시간, 공간 복잡도를 가진다. 그렇기 때문에 모델의 크기나 입력으로 사용하는 토큰의 수가 증가할때 복잡도가 증가하고 있다. Longformer, Performer, Reformer, Clustered attention들이 이러한 문제들을 해결하고자 시도했다.

이곳 허깅페이스에서 Linformer나 Performer들과 같은 다른 모델 들에 대한 설명도 확인 할수 있다.

BigBird는 block sparse attention을 적용해서 4096 토큰까지 사용할수 있게 했다. 최근의 GPT 계열의 모델들도 학습시 sparse attention을 사용한다고 나오기 때문에 큰 모델을 학습하고자할때 sparse attention을 알면 좋을거 같다. BigBird의 경우 기존의 BERT 모델이 사용한 full attention이 아닌 block sparse attention을 사용했으며 다양한 태스크에서 SOTA를 달성했다.

BigBird의 어텐션은 BERT의 attention을 근사하고자했으며 BERT의 attention보다 뛰어난 성능을 위한 것이 아닌 보다 효율적인 attention을 위해 노력했다.

버트와 같은 어텐션들은 아래와 같은 의문점들을 가진다.

입력으로 들어온 모든 토큰들이 다른 모든 토큰들에 대해서 어텐션 되어야하는가?
왜 중요한 토큰들에 대해서만 어텐션을 계산하지 않는가?
어떤 토큰들이 중요한지 어떻게 결정할 것인가?
선택된 몇가지 토큰들만 어텐션하기 위한 효율적인 방법은 어떻게 되는가?

1. 어떤 토큰들이 어텐션 되어야 하는가?

"BigBird는 허깅페이스에서 추출 QA에 대해 사용할 수 있다." 문장을 예시로 설명하고자 한다.

BERT 류의 어텐션에서는 모든 단어들에 대해 다른 모든 토큰들을 어텐션한다.

query-token \in {BigBird, 는, 허깅페이스, 에서, 추출, QA, 에, 대해, 사용할수있다}

의경우 다음 Key 토큰들에 대해서 어텐션을 한다.

key-token = [BigBird, 는, 허깅페이스, 에서, 추출, QA, 에, 대해, 사용할수있다]

약간의 수도코드와 함께 어떤 토큰들이 어텐션 되기위해 합리적인 선택인지 생각해본다. 예로 위 문장에서 "허깅페이스" 토큰이 쿼리될 수 있는것을 가정하고, 어텐션 할 key token들을 만든다.

# let's consider following sentence as an example
example = '['BigBird', '는', '허깅페이스', '에서', '추출', 'QA', '에', '대해', '사용할수있다']'

# futher let's assume we're trying to understand the representation of 'available
' i.e. 이 포스트에서는 허깅페이스로 변경
query_token = '허깅페이스'

# We will initialize an empty set and fill up the token of our interest as we proceed in this section
key_tokens = [] # => currently 'available' token doesn't have anything to attend

문장에서 토큰들은 근접한 이전과 이후 토큰들에 대해 높은 영향을 받기 때문에 근처의 토큰들은 매우 중요하다. 이러한 아이디어에 기반해서 sliding attention이 착안 되었다.

# window_size = 3으로 가정하고 '허깅페이스' 토큰의 좌우 한 토큰씩 고려한다
# left token = '는'; right token = '에서'
sliding_tokens = ['는', '허깅페이스', '에서']

# 위의 토큰들로 어텐션할 key_token들 업데이트
key_tokens.append(sliding_tokens)

Long-range dependencies, 긴 길이의 토큰들에 대한 의존성:어떤 태스크들의 경우 꼭 근처에 있는 토큰들만 중요한것이 아니라 먼 곳의 토큰들에 대한 관계도 포착해야할 때가 있다. QA 모델의 경우 전체 질문에 대해 어떤 문맥이나 토큰들이 중요한지 알기 위해 각 토큰들을 비교할 필요가 있다.

따라서, 빅버드 모델은 위와 같은 문제를 보완하기 위해 계산적인 효율성을 유지하면서도 먼토큰들을 고려할 수 있는 2가지 방법을 제시한다.

① Global tokens

모든 토큰들이 어텐션 되어야 하는 문장을 예를 들어 설명한다. "허킹페이스는 쉬운 NLP를 위한 멋진 라이브러리를 만든다" 라는 문장에서 "만든다"를 global token으로 정의 하면 '허깅페이스'와 '라이브러리' 토큰 간에는 관계를 알 필요성이 있다. 문장내에서 허깅페이스와 라이브러리 토큰은 서로 먼 거리를 가지고 있다. 따라서 '만든다' 토큰을 글로벌하게 어텐션할 수 있도록 한다.

# 첫번째와 마지막 토큰을 글로벌 토큰으로 가정한다.
global_tokens = ['BigBird', '사용할수있다']

# 글로벌 토큰들을 key token에 추가한다.
key_tokens.append(global_tokens)

② Random tokens

정보를 다른 토큰으로 전송할 어떤 토큰들을 랜덤하게 생성하고 다른토큰으로 전송할 수 있다. 이러한 방법은 토큰들간의 정보 전달의 비용을 줄여준다.

# 'r'은 예제 문장에서 몇개의 토큰을 랜덤으로 할지 
# r = 1 에 '에' 토큰 선택
random_tokens = ['에']

# 랜덤 토큰도 key_tokens에 추가
key_tokens.append(random_tokens)

# 이제 추가된 key_tokens의 리스트들을 본다
# print(key_tokens)
# {'BigBird', '사용할수있다', '에', '는', '허깅페이스', '에서'}

# 이제 '사용할수있다' 토큰은 전체 문장에대해 어텐션하는 것이 아닌 위의 토큰들에 대해서만 어텐션 할수 있다.

이러한 방법은 full attention에 근사하면서도 쿼리토큰이 전체 가능한 모든 토큰들에서 부분집합들에 대해서만 어텐션 할수 있다. 동일한 접근법이 모든 다른 쿼리 토큰들에 대해서도 사용될수 있다. 하지만 기억해야할것은, BERT의 full attention을 최대한 근사하는것에 있다. BERT가 하는것과 같이 쿼리 토큰이 모든 키 토큰들에 대해 어텐션하는 것을 단순하게 만드는 것은 GPU와 같은 현대적인 하드웨어 에서 행렬들의 시퀀스 곱셈 계산을 매우 효율적으로 처리할 수 있다.

하지만 sliding, global, random attention의 조합은 sparse한 행렬 곱을 의미하며 이것은 현대적인 하드웨어에서 효율성 달성을 어렵게한다.

BigBird의 주요한 공헌은 sliding, global, random attention 계산을 빠르게 할 수 있는 block sparse attention의 비율을 제시한것에 있다.

2. 그래프로 global, sliding, random keys 이해

global, sliding, random attention에 대해 보다 나은 이해를 얻기위해 그래프를 사용한다. 그리고 어떻게 이 세 어텐션이 표준적으로 사용되는 어텐션과 비교하여 훌륭하게 근사하는지 살펴본다.

Global connection

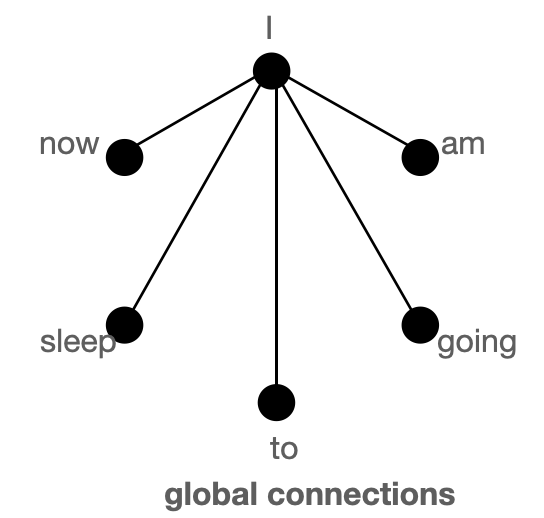
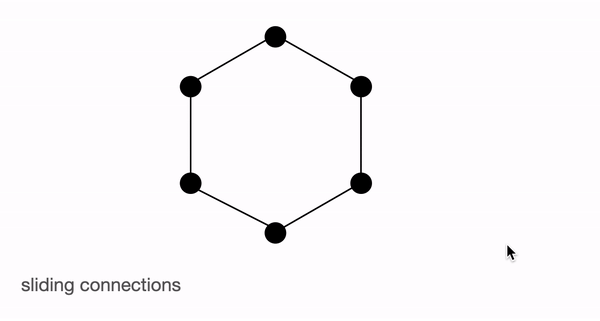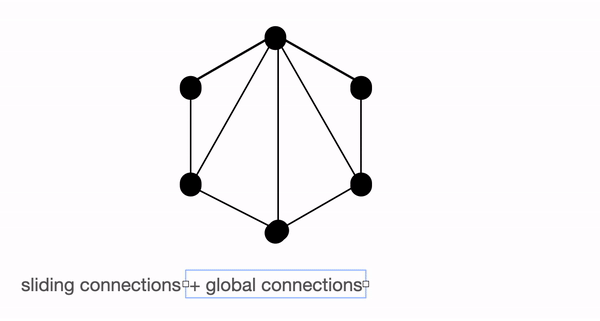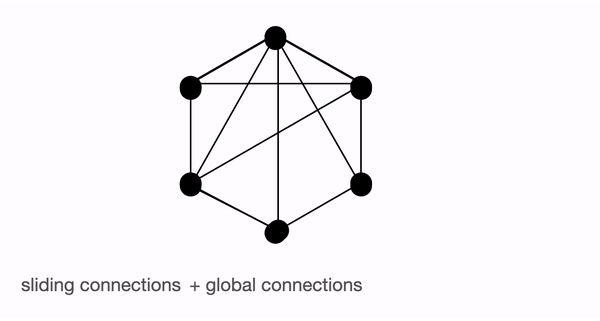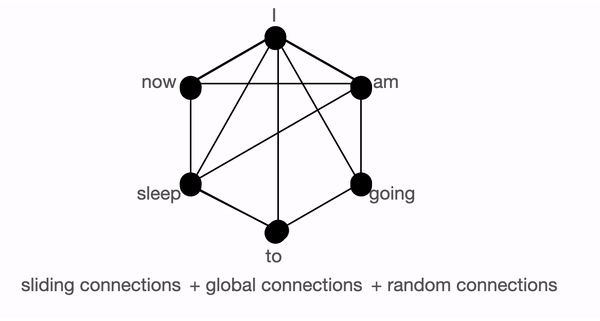
Sliding connection

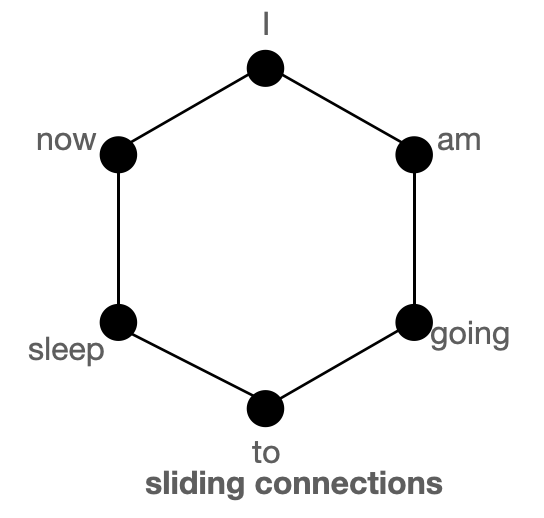
Random connection

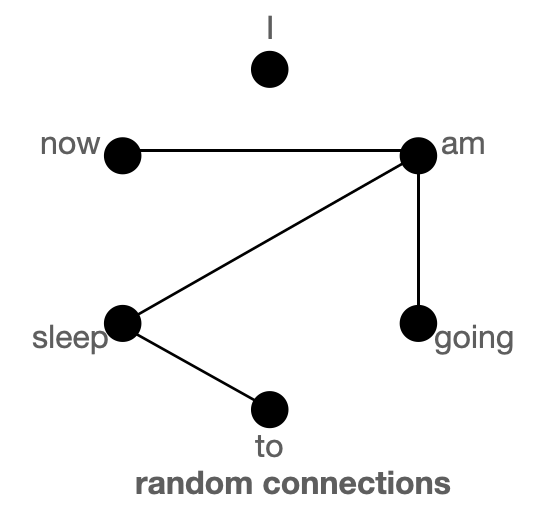
위의 그림들은 global, sliding, random connection들의 모습을 보이며, 노드는 토큰, 라인은 어텐션 스코어를 나타낸다. 두 노드간의 연결이 없으면 어텐션 스코어는 0을 나타낸다.

connection들의 합, Block Sparse Attention

Full connection

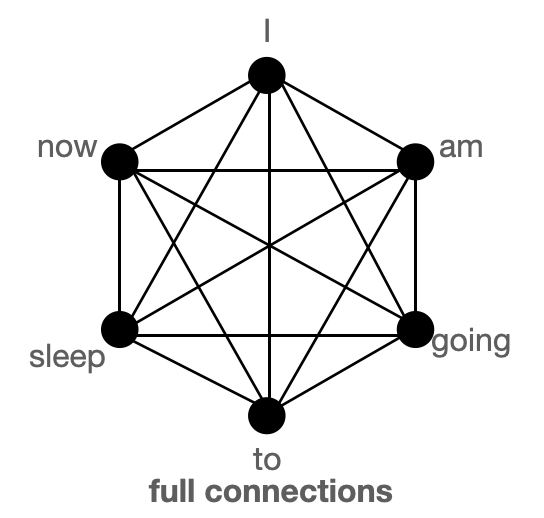
BigBird의 block sparse attention은 총 10 커넥션들로 global, sliding, random connection을 조합이다. 하지만 아래의 full connection을 보명 15 커넥션인 것을 볼수 있다.

Normal attention

모든 토큰들에 대해 각 토큰들이 쿼리 되고 어텐션 되기 때문에 싱글 레이어에서 모델은 한 토큰에서 다른 토큰으로 정보를 전달할 수 있다. 위의 그림을 통해 보자면 모델이 'going'과 'now' 연관을 필요로 할때, 그림에서는 토큰 사이에 커넥션이 있기 때문에 바로 정보를 전달할 수 있음을 볼수 있다.

Block sparse attention

위 그림에서 두 노드들 간에 정보를 공유하고자 할때, 싱글 레이어 안에서 모든 노드들이 직접 연결되어 있지 않기 때문에 다양한 노드들을 가로질러 정보를 전달해야한다. 'going'과 'now' 간에 연관을 보고자 할때 sliding attention의 경우 going -> am -> i -> now 와 같은 흐름으로 경로를 볼수 있다. 그결과 우리는 문장에서 전체 정보를 포착하기 위해서는 여러 레이어를 필요로 한다. 하지만 normal attention에서는 싱글 레이어에서 모든 토큰에 어텐션 할 수 있다.

global connection에서는 going -> i -> now 인 경로를 볼수 있고 random connection의 경우 going -> am -> now인 경로를 볼 수 있다. 이러한 점을 볼때 global과 random connenction을 통해 보다 적은 레이어로 정보를 전달할수 있음을 알 수 있다.

global 토큰이 많은 경우, global connection으로도 정보를 전달하기에 충분하기 때문에 random connection이 필요하지 않을 수 있다. 이러한 아이디어는 다양한 BigBird가 동작할때 num_random_tokens = 0 으로 유지하는 방법.

토큰 A가 B를 어텐션할수 있고, 토큰 B도 A를 어텐션할 수 있기 때문에 그래프 상에서 attention matrix는 대칭을 가정한다. $A_{ij} = A_{ji}$ .

Full Attention과 Block Sparse Attention 비교

Attention Type	global_tokens	sliding_tokens	random_tokens
full attention	n	0	0
Block Sparse Attention	2xblock_size	3xblock_size	num_random_block x block_size

도표에서 나온 block_size는 이후의 섹션에서 다루도록 한다.

3. BigBird Block Sparse Attention

BigBird의 block sparse attention은 토큰들이 모든 토큰들에 대해서 어텐션 하는것이 아닌 global tokens, sliding tokens, random tokens에 대해서 어텐션을 수행해 기존의 full attention 대비 효율성을 얻을 수 있었습니다.

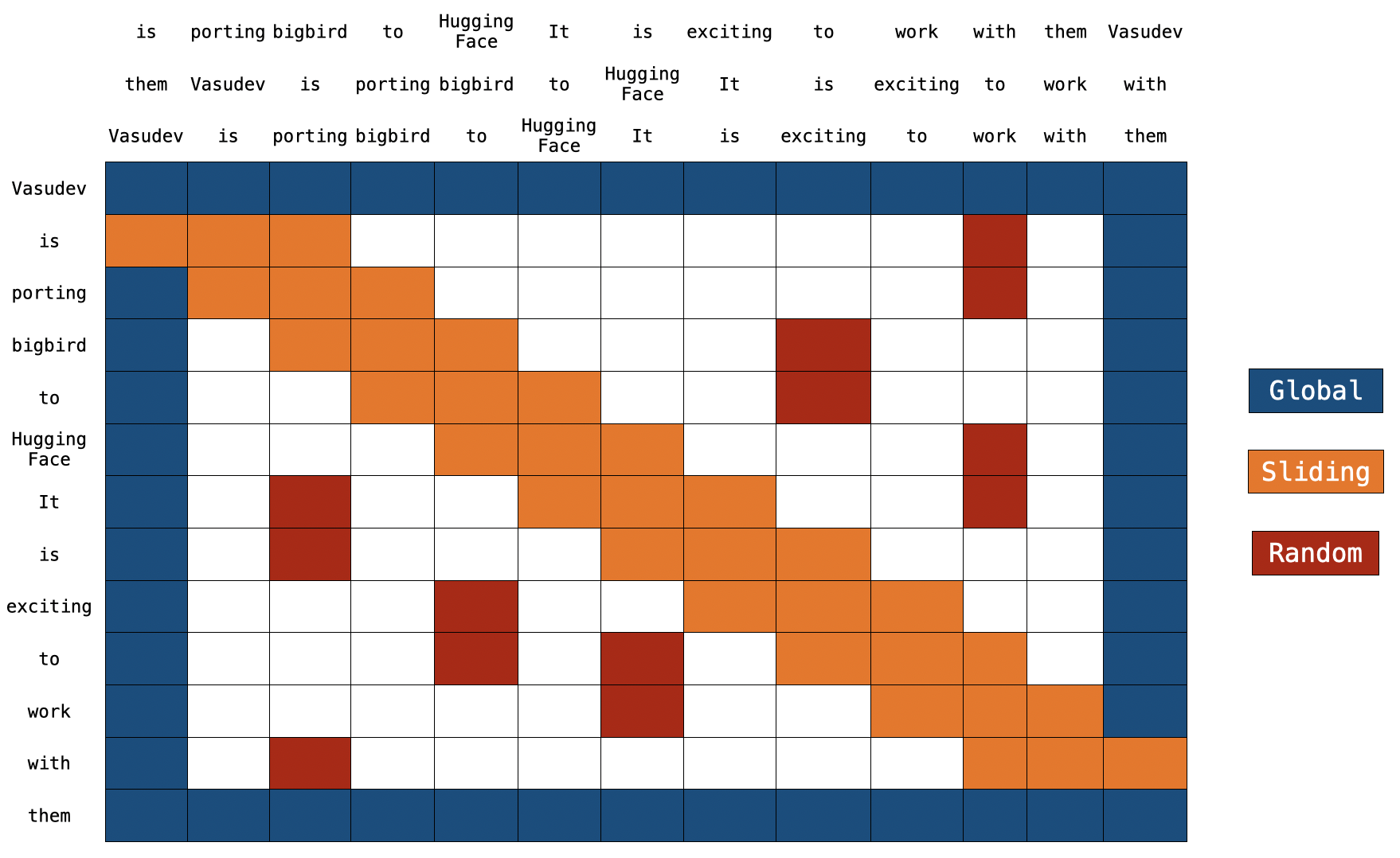
위의 그림을 보면 상단에 2개의 추가적인 문장을 볼수 있다. 두 문장은 자세히보면 한 토큰씩 이동 된것을 볼 수 있으며, 이것을 통해 어떻게 sliding attention이 동작 하는지 알 수 있다. q[i] 을 k[i,0:3] 으로 곱하면 q[i] 에 대한 sliding attention score를 얻을 수 있다. 이때 i 는 문장 내에서 토큰의 인덱스이다.

만약 block sparse attention에 대해 실제 구현체를 찾는다면, 이곳을 확인하면된다. 지금으로써는 구현체의 코드를 보는게 이해가 되지 않을 수 있지만 허깅페이스의 bigbird 포스트를 다 읽고 이해하고 나면 보다 쉽게 이해할 수 있을것이다.

Global Attention

global attention에서 각 쿼리는 문장 내에 있는 다른 모든 토큰들에 어텐션 하고 어텐션 되어진다.위 그림의 문장에서 Vasudev (첫번째 토큰) & then(마지막토큰)이 global 토큰이라 가정해보자. 그림에서 푸른 박스를 보면 모든 토큰들에 대해 어텐션 된것을 볼 수 있다.

# pseudo code
Q -> Query matrix (seq_length, head_dim)
K -> Key matrix (seq_length, head_dim)

# 첫번째 토큰과 마지막 토큰은 다른 모든 토큰들에 어텐션한다.
Q[0] x [K[0], K[1], K[2], ... , K[n-1]]
Q[n-1] x [K[0], K[1], K[2], ... , K[n-1]]

# 첫번째 토큰과 마지막토큰이 다른 모든 토큰들에 어텐션 되어진다.
K[0] x [Q[0], Q[1], Q[2], ... , Q[n-1]]
K[n-1] x [Q[0], Q[1], Q[2], ... , Q[n-1]]

Sliding Attention

슬라이딩 어텐션을 구현하기 위해 문장의 키 토큰들을 2번 복사되어, 한번은 오른쪽으로 한칸 이동 되어지고, 다른 한번은 왼쪽으로 한칸 이동 된다. 만약 어텐션에서 쿼리로 들어온 문장을 3 문장으로 곱하게 된다면 모든 sliding token을 다루게 된다. 그리고 계산 복잡도 또한 단순하게 $O(3n) = O(n)$ 으로 볼수 있다.

위 그림에서 오렌지색 박스가 sliding attention을 나타내며 3 문장이 각각 복사되어 왼쪽,오른쪽으로 이동한것을 볼수 있다.

# What we want to do
Q[i] x [K[i-1], K[i], K[i+1]] for i = 1:-1

# efficient inplementation in code (assume dot product multiplication 👇)
[Q[0], Q[1], Q[2], ......, Q[n-2], Q[n-1]] x [K[1], K[2], K[3], ......, K[n-1], K[0]]
[Q[0], Q[1], Q[2], ......, Q[n-1]] x [K[n-1], K[0], K[1], ......, K[n-2]]
[Q[0], Q[1], Q[2], ......, Q[n-1]] x [K[0], K[1], K[2], ......, K[n-1]]

# 각 시퀀스는 3 문장에 대해서 곱해진다.
# 몇가지 계산이 빠졌을 수 있으며, 이코드는 대략적인 아이디어를 보여준다.

Random Attention

랜덤 어텐션은 각 쿼리가 몇몇 랜덤 토큰들에 대해서만 실제적으로 어텐션 되어지는것을 말한다. 이것은 모델이 어떤 토큰들을 랜덤하게 모으고, 그들의 어텐션 스코어를 계산한다.

# r1, r2, r은 ramdom indices 
Q[1] x [Q[r1, Q[r2], ... Q[r]]
.
.
.
Q[n-2] x [Q[r1, Q[r2], ... Q[r]]

# 0번째, 마지막 토큰은 이미 global token으로 제외한다.

Implementation

기존의 attention에선 $ X = x_1, x_2, ..., x_n$ 과 같은 토큰들의 시퀀스들이 Dense layer를 통해 $Q, K, V$ 가 되고, 그후 attention score $Z$ 가 $Z=softmax(QK^T)$ 와 같이 계산된다. 하지만 BigBird에서 사용되는 Block Sparse Attention의 경우 같은 어텐션 계산 절차를 따르지만 query와 key vector 선택 부분에서 차이가 있다.

bigbird의 block sparse attention이 어떻게 동작하는지 살펴보자. 아래의 값들을 정한다.

구분	파라미터
$b$	`block_size`
$r$	`num_random_blocks`
$s$	`num_sliding_blocks`
$g$	`num_global_blocks`

일때, $b=4, r=1, g=2, s=3, d=5$ 으로 정한다.

$q_1, q_2,q_{3:n-2},q_{n-1},q_n$ 의 attention score는 아래와 같이 분리되어 계산된다

$a=softmax(q_1*K^T)$ 와 같을 때, $a_1$ 에 대한 $q_1$ 의 attention score는 첫번째 블록안의 모든 토큰들과 문장 안의 다른 모든 토큰들 사이의 attention score이다.

$q_1$ 은 첫번째 블록을 나타내며 , $g_i$ 는 $i$ 번째 블록을 나타낸다. 이렇게 구한 $q_i$ 와 $g_i$ 를 이용해 일반 attention을 수행한다

두번째 블록에 대해서 attention score를 계산할때 처음 세 블록, 다섯번째 블록, 마지막 블록을 모은다. 그리고 attention score $a2 = softmax(q_2 * concat(k_1, k_2, k_3, k_5, k_7))$ 을 구한다.

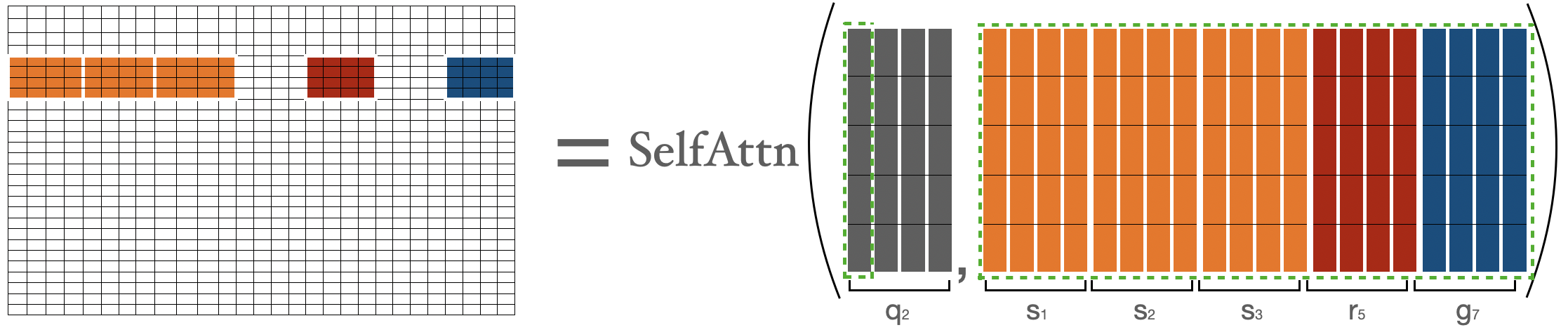
(global token, random token, sliding token)의 표현을 $g, r, s$ 으로 나타낸다.

$q_{3:n-2}$ 에 대한 attention score를 계산하기 위해, global, sliding, random key들을 모으고 $q_{3:n-2}$ 과 모아진 key들에 대해 기본 attentnion을 계산한다. sliding key들은 앞서 소개한 shifting trick을 이용해 모아진다.

이전의 블록의 마지막 블록의 토큰( $q_{n-1}$ )들의 attention score를 계산하기 위해, 첫번째 블록, 마지막 세 블록, 세번째 블록을 모은다. 그리고 $a_{n-1} = softmax(q_{n-1} * concat(k_1, k_3, k_5, k_6, k_7))$ 과 같이 계산할 수 있다.

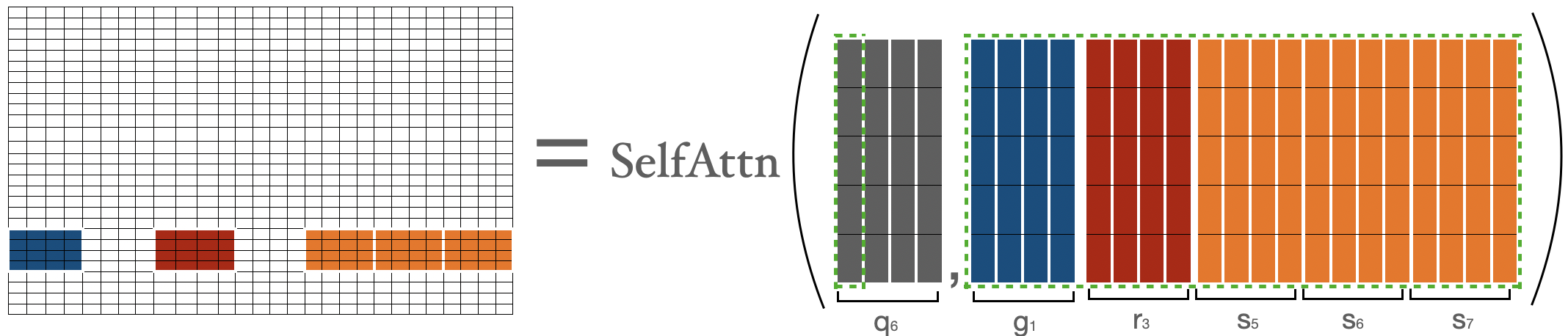
$a_n = softmax(q_n * K^T)$ 일때, $a_n$ 에 대한 $q_n$ 의 attention score는 마지막 블록에서 모든 토큰들과 시퀀스 안의 다른 모든 토큰들에 대한 attention 결과이다. 이 계산 절차는 $q_1$ 의 attention score를 구한것과 유사하다.

위에서 최종 어텐션 매트릭스를 얻기 위해 위에서 살펴본 matrix들을 합쳐본다. 모든 토큰에 대한 representation을 얻기 위해 합쳐진 attention matrix을 사용 할 수 있다.

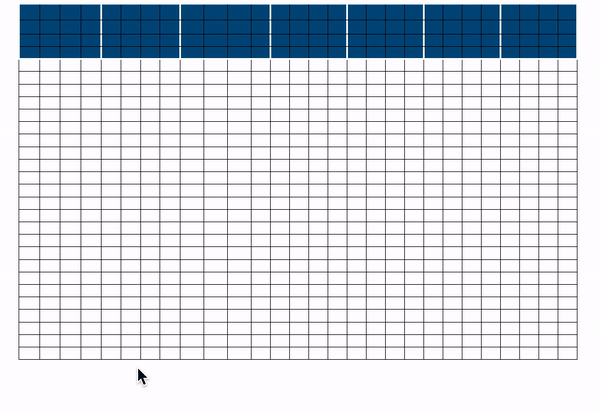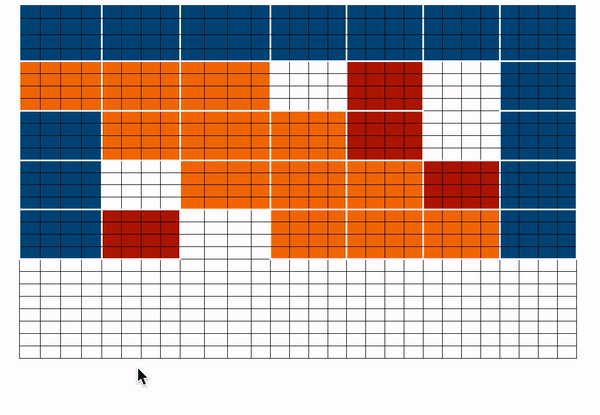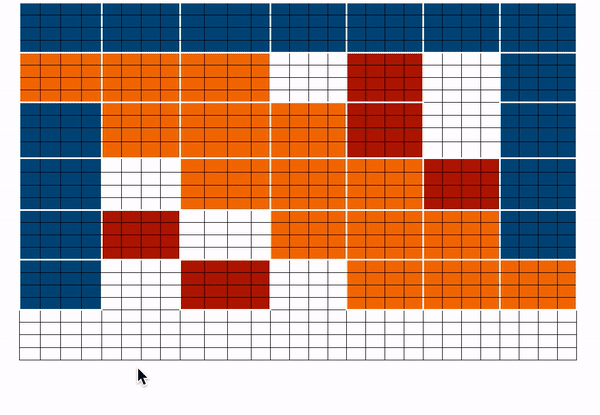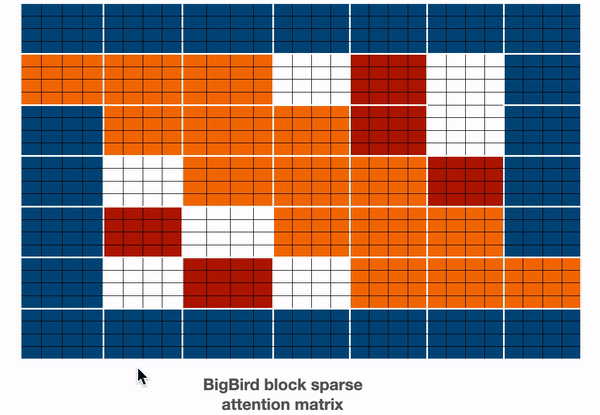
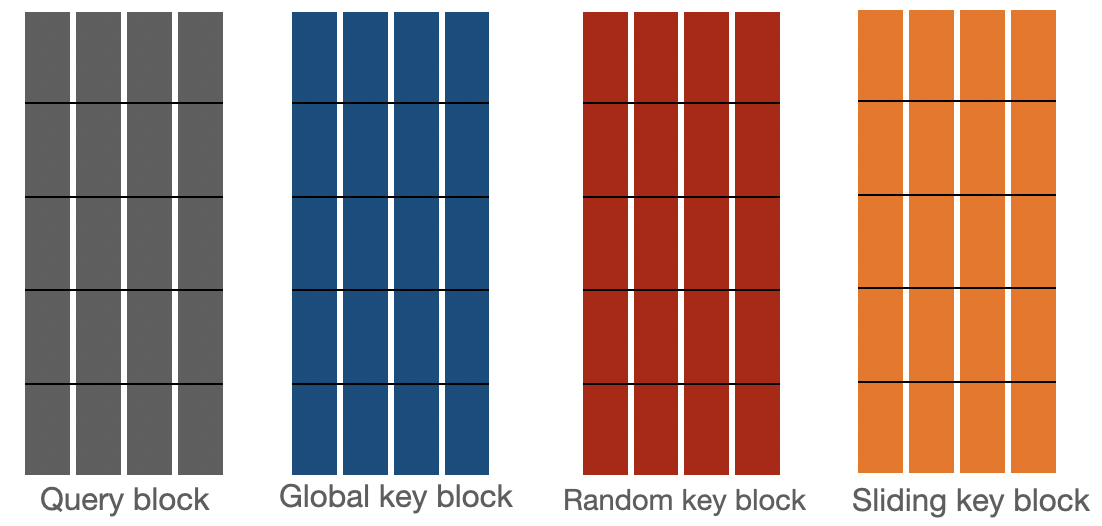
blue -> global blocks
red -> random blocks
orange -> sliding blocks

위와같이 어텐션 매트릭스를 볼 수 있으며, forward pass가 진행 되는 동안 white blocks들은 저장하지 않는다. 하지만 각 토큰의 representation을 나타내는 value matrix을 계산하는데는 사용한다.

마무리

지금까지 block sparse attention의 가장 어려운 부분인 implementation 을 살펴보았다. 지금까지의 내용을 통해 bigbird의 block sparse attention 의 코드를 보며 이해할수 있는 기본 지식을 얻었다.

Time & Memory complexity

Attention Type	Sequence length	Time & Memory Complexity
full attention	512	T
	1024	4 X T
	4096	64 X T
block_sparse	1024	2 x T
	4096	8 x T

ITC vs ETC

빅버드를 학습시키는데 사용하는 2가지 전략이다.

nawnoes

이전 포스트

BlenderBot 2.0: 장기 기억 메모리와 인터넷 검색을 활용한 오픈소스 챗봇

다음 포스트