기울기 소실 (Gradient Vanishing)
역전파 과정에서 입력층으로 갈수록, 기울기가 점차적으로 작아지는 현상이 발생할 수 있다. 이러한 현상으로 입력층에 가까운 층들에서 가중치들이 업데이트가 제대로 되지 않으면 결국 최적의 모델을 찾을 수 없게 되고, 이것을 기울기 소실이라 한다.
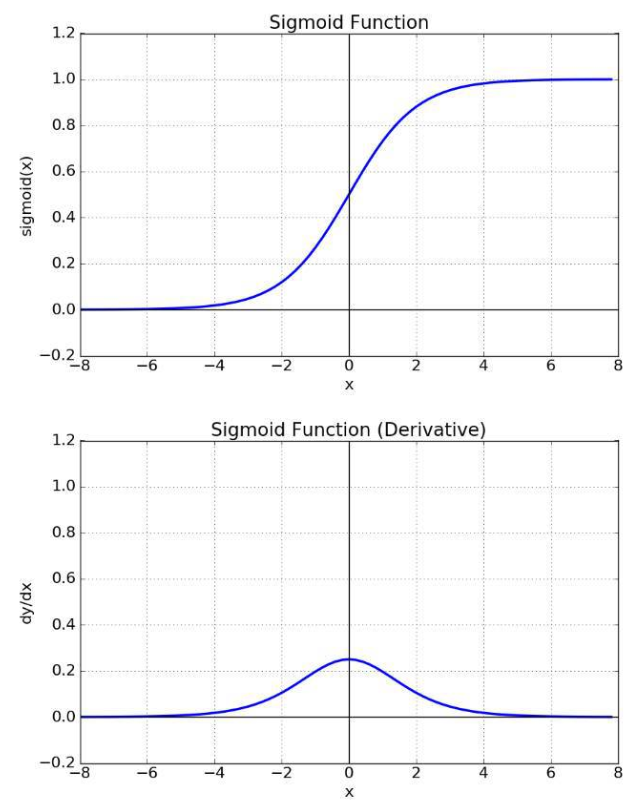
활성화함수 중 sigmoid를 사용하게 되면, 해당 함수의 특성에 따라 기울기가 0에 수렴하여 나타나는 경우가 발생한다. 따라서 역전파에서 입력층으로 갈수록 sigmoid함수의 미분을 연쇄적으로 곱하게 될때, 그 값은 1보다 작은 값들이므로 곱할수록 값이 점점 작아지게 된다. layer가 많으면 많을수록 기울기 값은 0에 가깝게 작아져서 가중치의 변화가 거의 없게 되고, error값도 더이상 줄어들지 않게된다.
기울기 폭주 (Gradient Exploding)
기울기 소실과 반대로, 기울기가 입력층으로 갈수록 점차 커지다가 가중치들이 비정상적으로 큰 값이 되면서 발산되는 현상이다.
기울기 소실과 폭주 방지
활성화함수 ReLU / Leaky ReLU 사용
기울기 소실에서 sigmoid 활성화함수를 사용하여 기울기가 0에 수렴하는 문제가 있었다. 그래서 역전파과정에서 전파시킬 기울기가 점점 사라진다는 문제가 있었는데, 이를 해결하기 위해 hidden layer의 활성화함수로 sigmoid나 tanh대신 ReLU나 ReLU의 변형함수인 Leaky ReLU를 사용하는 것이다.
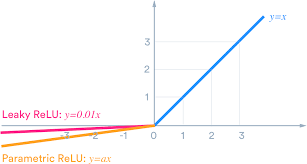
특히 Leaky ReLU를 사용하면 모든 입력값에 대해 기울기가 0에 수렴하지 않으므로 죽은 ReLU문제를 해결할 수 있다.
그래디언트 클리핑 (Gradient Clipping)
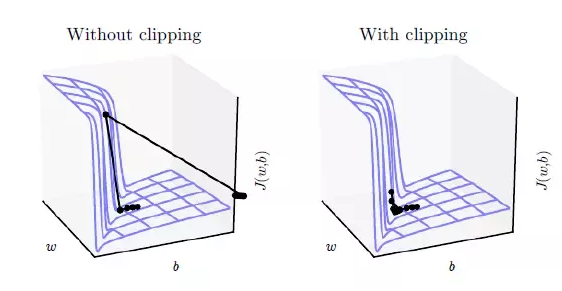
그래디언트 클리핑이란 기울기 값을 자르는 것을 의미한다. 기울기 폭주를 막기 위해서 특정 threshold를 넘지 않도록 값을 잘라 threshold만큼 크기를 감소시키는 것이다. 클리핑은 기울기의 L2norm으로 나눠주는 방식으로 하게되는데, threshold는 gradient가 가질 수 있는 최대 L2norm을 뜻한다.
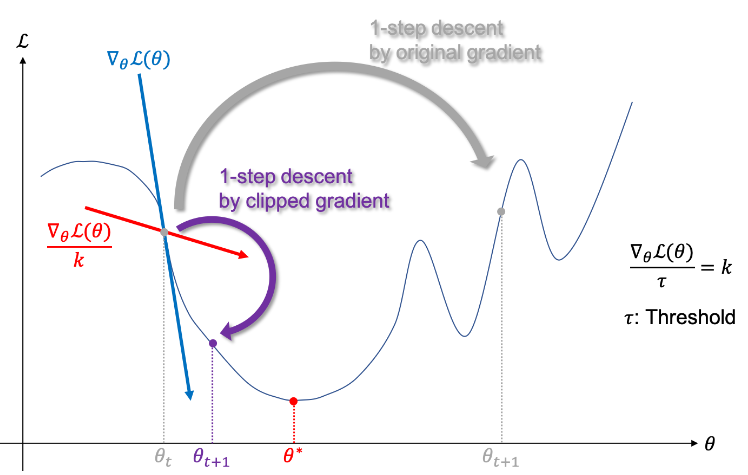
위 그림처럼 기울기가 많이 뛰어서 global minimum에 도달하지 못하고 엉뚱한 방향으로 가는 것을 클리핑이 막아준다. 이때 gradient vector의 방향은 유지하면서 적은 값만큼 안정적으로 이동할 수 있다.
가중치 초기화 (Weight initialization)
같은 모델을 훈련하더라도 가중치가 초기에 어떤 값을 가졌느냐에 따라 모델의 훈련결과가 달라지기도 한다. 초기값을 0으로 하면 역전파 계산시 모든 가중치의 값이 똑같이 갱신되므로 적절한 가중치로 초기화하는 것이 중요하다.
세이비어 초기화 (Xavier Initialization)
이전 Layer의 노드 수와 다음 Layer의 노드 수에 따라 가중치를 결정 짓는 방법이다. Uniform 분포를 따르는 방법으로 초기화하는 방법과, Normal 분포를 따르는 방법 두가지가 사용된다.
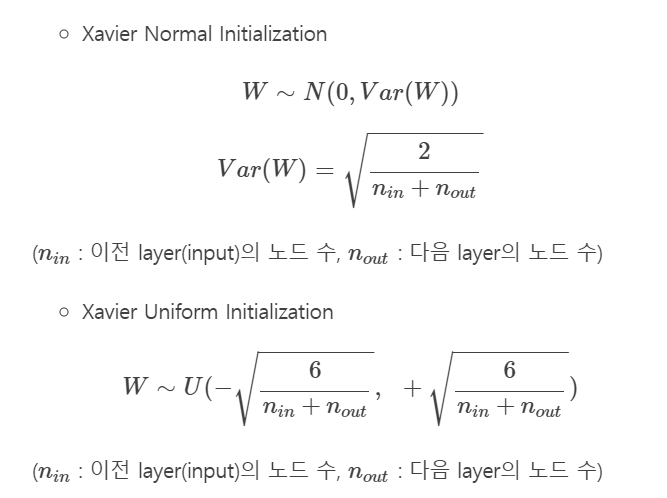
세이비어 초기화는 여러층의 기울기 분산 사이에 균형을 맞춰 특정층이 너무 주목을 받거나 다른 층이 뒤쳐지는 것을 막는다.
S자 형태인 활성화 함수와 함께 사용할 때는 좋은 성능을 보이지만, ReLU와 함께 사용하면 성능이 좋지 않다.
He 초기화 (He Initialization)
세이비어 초기화에서는 ReLU함수를 사용할 때 비효율적이라는 것을 보이는데, 이것을 보완한 기법이다. 이때는 다음층의 뉴런수를 반영하지 않으며 여기서도 Uniform 분포를 따르는 방법으로 초기화하는 방법과, Normal 분포를 따르는 방법 두가지가 사용된다.

He 초기화 + ReLU가 보편적이라고 한다.
배치 정규화 (Batch Normalization)
배치정규화는 인공신경망의 각 층에 들어가는 입력을 평균과 분산으로 정규화하여 학습을 효율적으로 만든다. 각 층에서 활성화 함수를 통과하기 전에 수행된다.
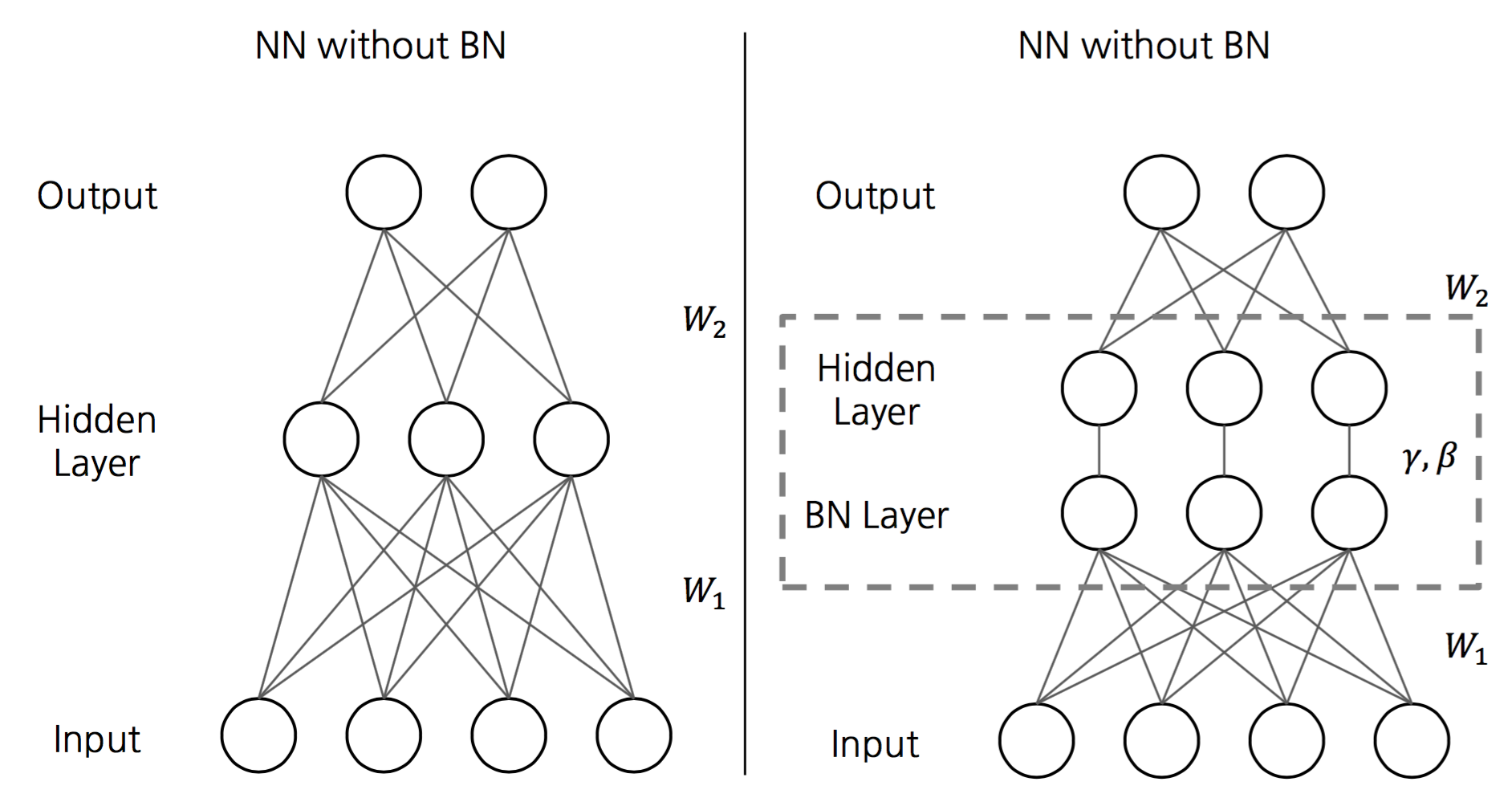
학습시 배치단위의 평균과 분산들을 차례대로 받아 이동평균과 이동분산을 저장해놓았다가, 테스트할때는 해당배치의 평균과 분산을 구하지 않고 구해두었던 평균과 분산으로 정규화를 한다.
정규화를 통해 입력분포를 일정하게 만들기 때문에 가중치를 일관되게 계산할 수 있다. 미니배치마다 평균과 표준편차를 계산하여 사용하므로, 오버피팅을 방지할 수도 있으며, 드롭아웃과 비슷한 효과를 낼 수 있다.
그러나 배치정규화는 미니배치 크기에 의존적이며, RNN에 적응하기 어렵다는 단점이 있다. (각 시점마다 다른 통계치를 가지기 때문이라고 함.)
층 정규화 (Layer Normalization)
따라서 층 정규화 라는 방법이 소개된다.
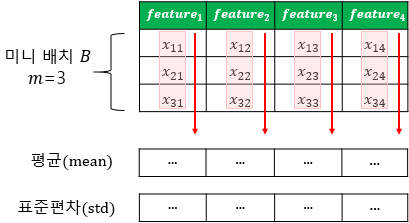
위 그림은 배치정규화를 시각화한 그림

층 정규화는 데이터별로 정규화하는 것이다.
