활성화함수의 필요성
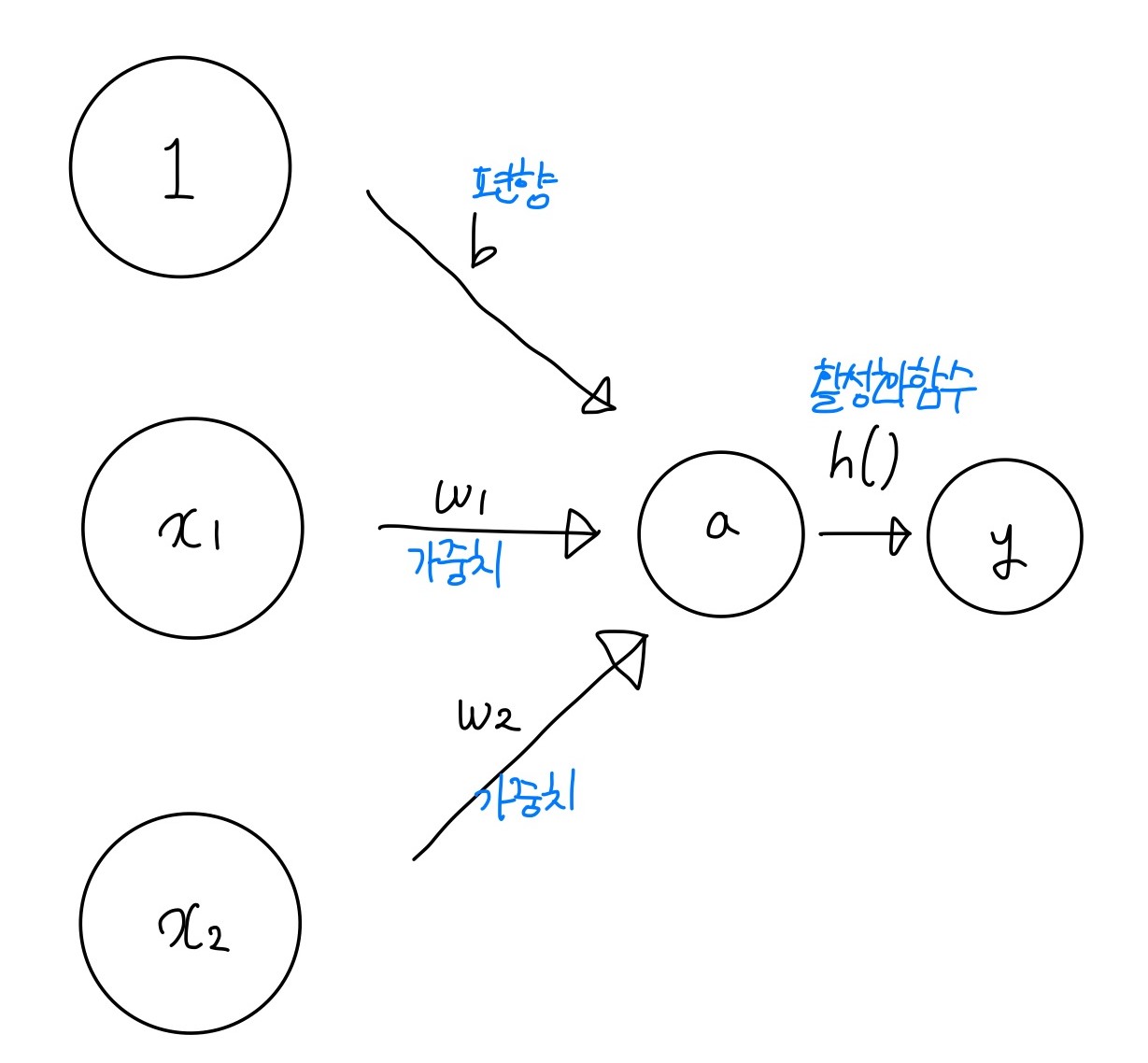
우선 퍼셉트론에서, x1와 x2를 입력받아 y를 출력하게 된다. 이때 b라는 편향을 통해 퍼셉트론이 얼마나 쉽게 활성화 되는지에 대한 정도를 결정한다. 편향이 -1000이라면, 입력값이 1000이 넘어야 활성화 될 것이고, 편향이 -10이라면, 입력값이 10만 넘어도 쉽게 활성화 될 수 있다. 노이즈를 제거하기 위한 목적도 있는데, 노이즈만큼을 편향으로 주어 노이즈로 발생할 값들을 무시해주는 역할도 할 수 있다.
위 그림에서의 퍼셉트론은 x1, x2, 1이라는 세개의 신호가 뉴런에 입력되고 각 신호에 가중치를 곱한 후 다음 뉴런에 전달된다. 이 신호의 총합이 h()라는 함수를 거쳐 변환되고, 그 변환값이 y의 출력이 되는 것이다. 이때 h()처럼 입력 신호의 총합을 출력신호로 변환하는 함수를 활성화 함수라고 한다.
활성화함수는 훈련과정에서 계산량이 많고, 역전파(backpropagation)에서 사용된다. 각 활성화함수에서 계산된 미분값을 통해 backpropagation이 이루어지고, 이를 통해 손실을 줄이도록 최적화해 나간다.
비선형 활성함수의 필요성
이 활성화함수를 통해 비선형함수를 사용하여 레이어층을 깊게 표현할 수 있다. 선형함수를 사용하게 되면 아무리 층을 쌓아도, 결국 선형함수로만 표현되어 층을 쌓지 않아도 같은 선형함수로 표현가능하게 된다. 따라서 비선형함수를 사용하여, 각각의 층에서 적절한 학습이 이뤄지도록 한다.
활성화함수의 종류
선형 활성화함수
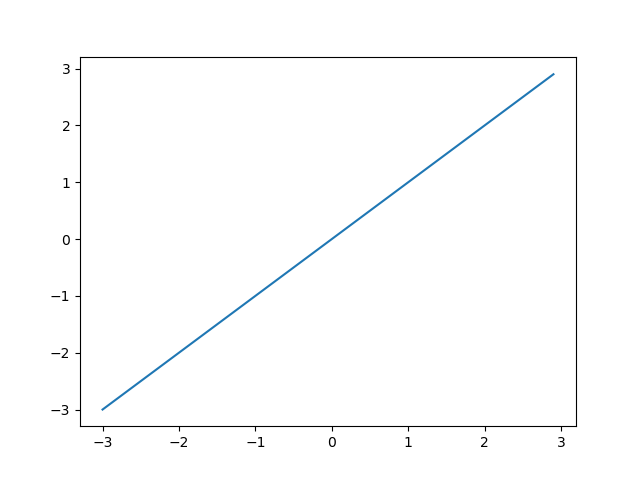
선형함수를 사용하면 다중출력이 가능해서 이진분류, 다중분류문제까지 해결가능하다.
그러나 비선형적 특성을 지닌 데이터를 예측하지 못한다. 특히 XOR gate 같은 그래프처럼 하나의 선으로 구분할 수 없는 경우를 구현하지 못한다.
비선형 활성화함수
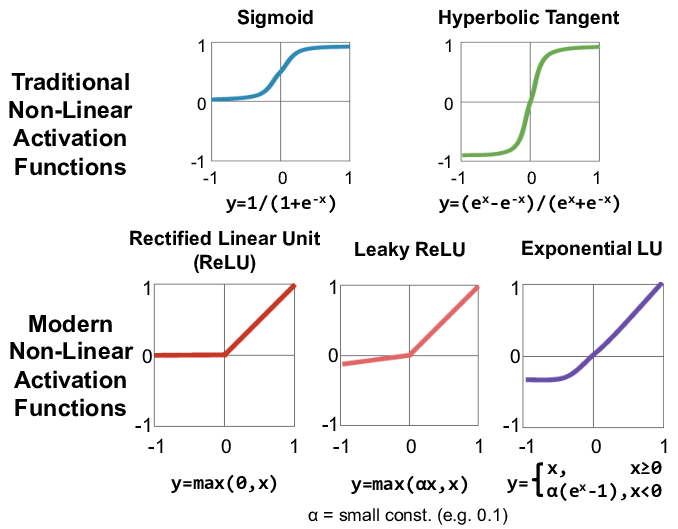
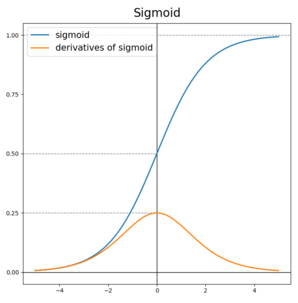
Sigmoid
수식
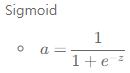
출력
0 에서 1사이 값
평균
0.5
특징
음수값을 0에 가깝게 표현하기 때문에, 입력값이 최종레이어에서 미치는 영향이 적어지는 Vanishing Gradient Problem 발생.
Vanishing Gradient Problem
기울기값이 사라지는 문제. 기울기가 사라진다면, 변화량이 없어진다는 것이고, 학습할 수 없는 상태가 된다는 것. error rate가 낮아지지 못하고 수렴해버리는 문제.
binary classification의 경우 출력층 노드가 1개이고, 이 노드 값은 0에서 1의 값을 가져야 하기 때문에, 시그모이드를 통해 0혹은 1의 값을 출력값으로 받을 수 있다.
은닉층에서는 시그모이드가 잘 사용되지 않는다.
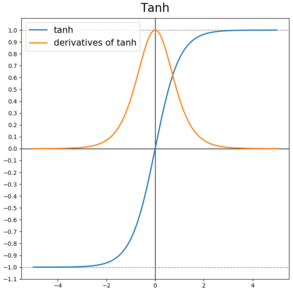
Tanh (Hyerbolic Tangent)
수식
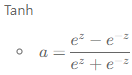
출력
-1 에서 1사이 값
평균
0
특징
평균이 0이므로 음과 양이 같은 편향을 가지도록 분포가 되어 있다. 0중심에서 기울기가 크기 때문에 값을 잘 보존한다.
이때도 시그모이드와 동일하게 Vanishing Gradient Problem이 나타난다.
Softmax Function
수식
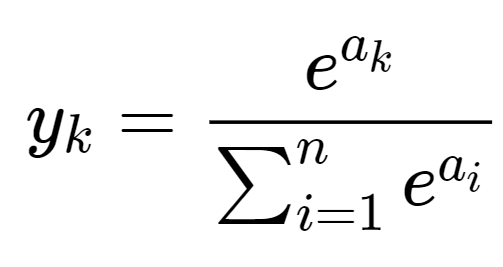
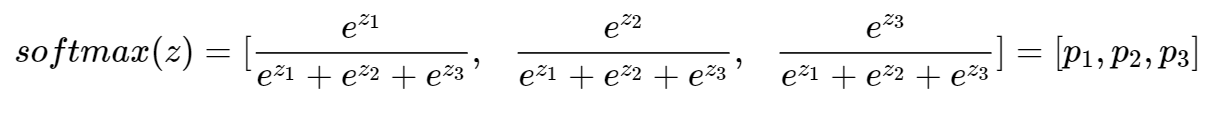
시그모이드 함수로부터 유도된 softmax 식
특징
소프트맥스는 세개 이상으로 분류하는 다중 클래스 분류에서 사용되는 활성화 함수이다. 분류될 클래스가 n개일 때, n차원의 벡터를 입력받아, 각 클래스에 속할 확률을 추정하게 된다.
ReLu (Rectified Linear Unit)
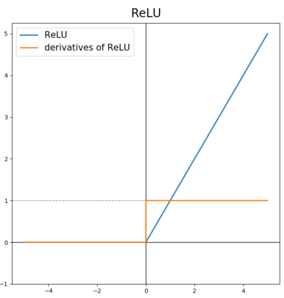
수식
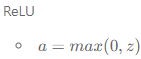
출력
0 에서 z
특징
가장 많이 사용되는 활성화함수이다.
대부분의 input값에 대한 기울기가 0이 아니므로, 학습이 빠르다. Sigmoid, Tanh와 달리, 기울기가 0이 되는 문제를 막아주기 때문에 학습이 빠르다.
input이 0보다 작은 경우 기울기가 0이 되는데, 실제로 hidden layer에서 대부분 노드의 z값은 0보다 크기 때문에 기울기가 0이 되는 경우가 많지 않다.
leaky ReLu
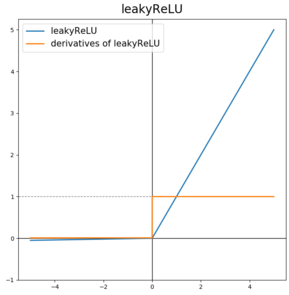
수식
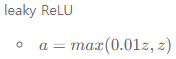
출력
0.01z 에서 z
특징
input값이 음수인 경우, 기울기가 0이 아닌 0.01 값을 가지게 되므로 ReLu보다 학습이 더 잘된다.
ELU (Exponential Linear Unit)
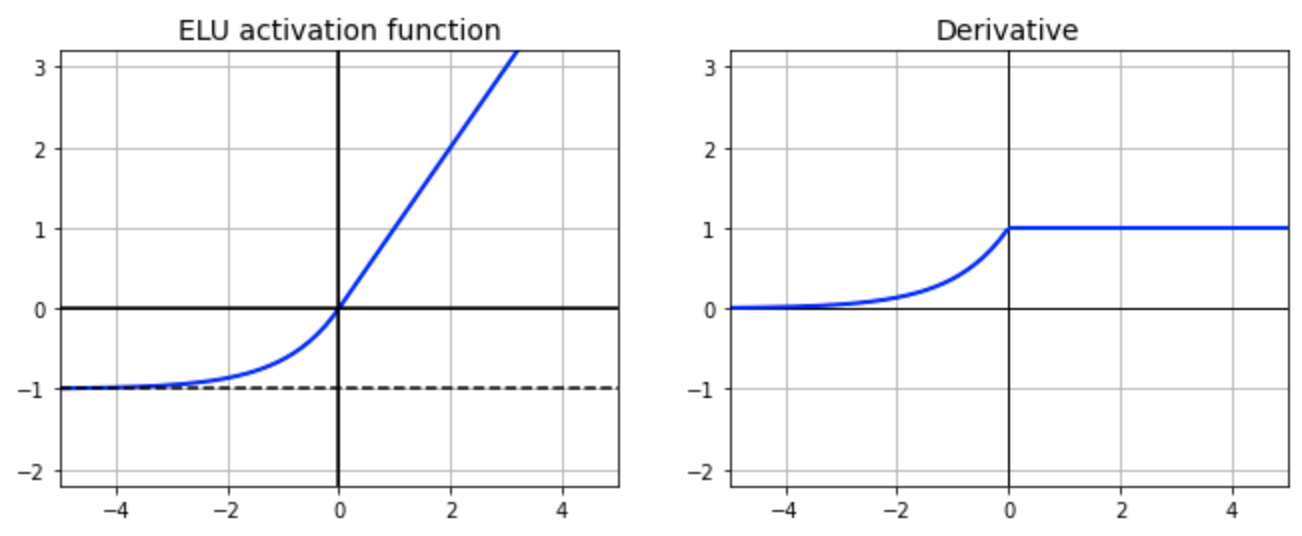
수식
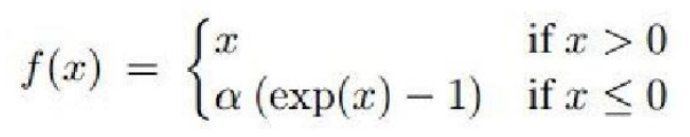
출력
-1에서 z
특징
leaky ReLu와 마찬가지로 입력값이 음수일 때 기울기가 0이 아닌 0에서 1사이 값으로 나타난다. leaky ReLu보다 큰 기울기로 수렴이 빠르다.
그러나 exponential 함수에 대한 연산비용이 필요하다.
활성화함수 구현과 특징 한계 실험 https://github.com/ai-rtistic/AIFFEL-Project/blob/master/Fundamental/FD23_Activation_Function.ipynb

