자료구조 개념
대량의 데이터를효율적으로 관리하기 위해,데이터를 저장및정렬하는방식데이터를 어떤 방식으로저장하고정렬하느냐에 따라추출 방식등데이터를 처리및조작하는데필요한 코드가달라진다
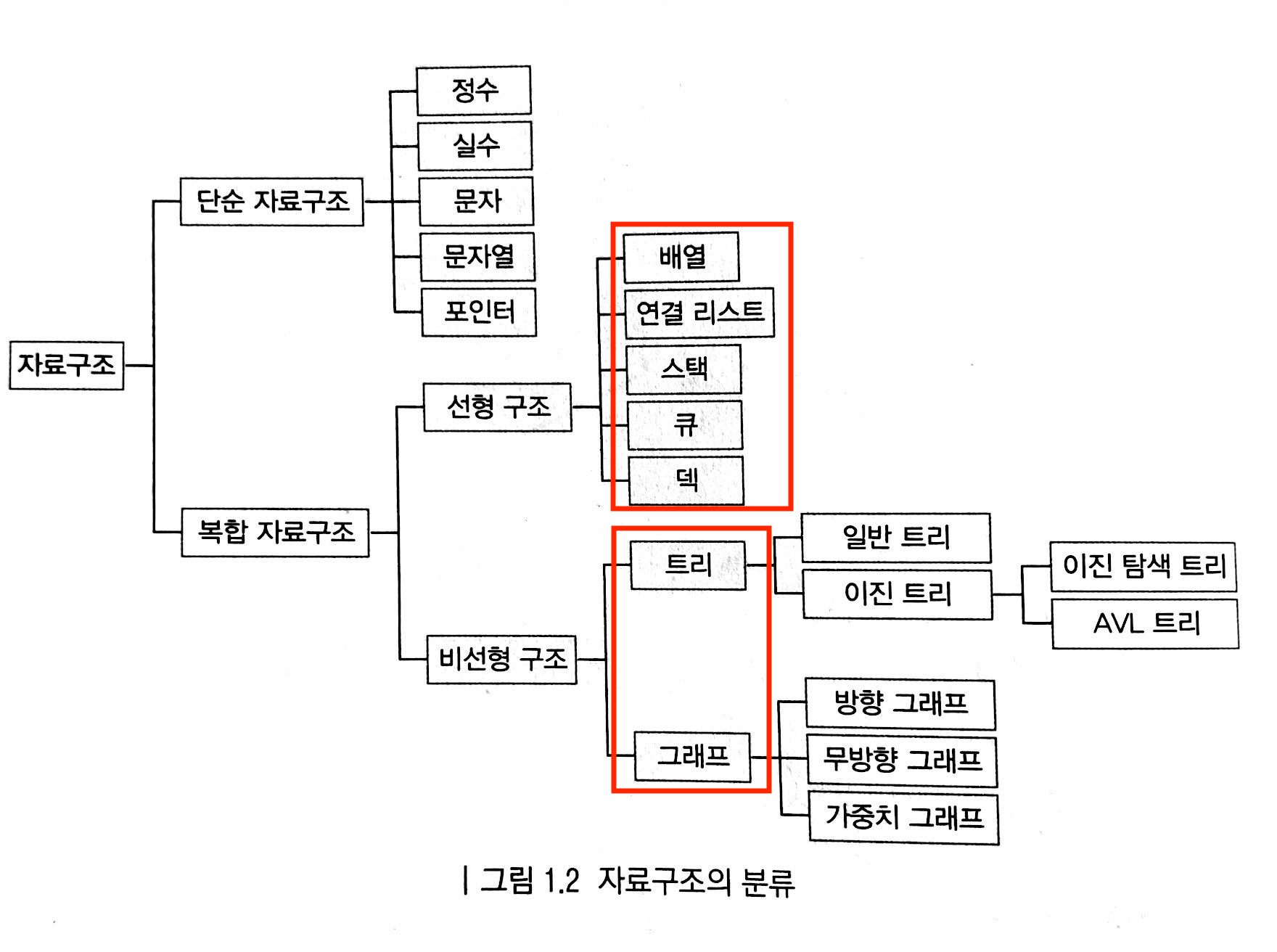
자료구조 분류
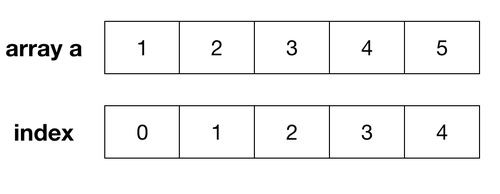
배열(Array)
한가지 데이터 타입의데이터를순차적으로저장 및 정렬하는자료구조각 데이터마다Index를 부여하여데이터 검색에용이(장점)배열은크기가고정적(단점)데이터가 삭제되면배열 전체의 데이터를 재정렬(단점)
리스트(List)
[ 선형 리스트(LinearList) ]
ArrayList라고 하기도 함
:배열(Array)처럼데이터들이 순서대로 늘어선 구조이기 때문데이터 접근이용이-->O(1)데이터 삽입/삭제가불리-->O(N)리스트의 크기가제한되어 있어서재조정하는 것은많은 비용 소요
[ 연결 리스트(LinkedList) ]
ref : https://beginnersbook.com/2013/12/linkedlist-in-java-with-example/
노드와포인터로구성배열(Array)의단점이보완된형태의 자료구조
-->크기가가변적인 배열(장점)포인터를 위한 저장 공간이따로 필요(단점)데이터 접근이불리-->O(N)데이터 삽입/삭제가용이-->O(1)두개의 포인터를 가진이중 연결리스트(Double Linked List)존재
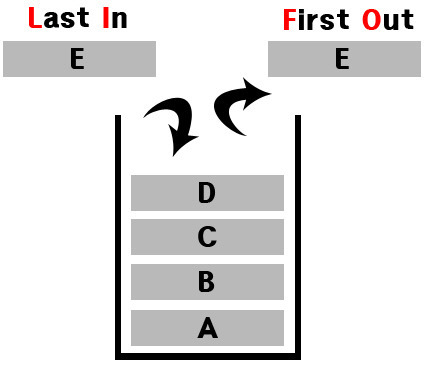
스택(Stack)
후입선출(LIFO)방식으로데이터를저장및정렬하는자료구조데이터의입력과출력이top에서만 가능- 사용 되는 곳
함수의 콜스택문자열 역순 출력연산자 후위표기법등
큐(queue)
ref : https://galid1.tistory.com/483
선입선출(FIFO)방식으로데이터를저장및정렬하는 자료구조데이터의 삽입은뒤에서만 /삭제는앞에서만가능- 사용되는 곳
OS의 프로세스 스케쥴링 방식을 구현하기 위해 사용버퍼
그래프(Graph)
ref :
https://sarah950716.tistory.com/12
개념
정점(V)과간선(E)으로 이루어진자료구조
종류
- 종류
- 방향 그래프
: 두 정점을 연결하는 간선에 방향이 존재하는 그래프
- 무방향 그래프
:
두 정점을 연결하는간선에방향이존재하지 않는 그래프- 가중치 그래프
:
두 정점을 이동할 때비용이드는 그래프
구현 방법
(무향 그래프인 경우)
인접 행렬(Array): 2차원 배열을 이용해서 구현
- 장점
두 정점에 대한 연결 정보를 조회할 때,O(1)소요- 구현이 쉽다
- 단점
특정 노드에 연결된노드를 확인하려면, 모든 노드를 확인해야 함 -->O(V)
(i번 노드에 연결된 것들을 확인하려면adj[i][1] ~ adj[i][V]를확인해야 함)V^2 만큼의메모리 공간이 항상 필요인접 리스트(List)
- 장점
실제로 연결된 노드에 대한메모리만 필요특정 노드에 연결된노드를 확인하려면,연결된 간선 만큼만 보면 됨 -->O(E)- 단점
두 정점에 대한 연결 정보를 조회할 때,O(V)소요
(i번 노드가j와 연결된 것을확인하려면adj[i]에 있는모든 정점을 확인해야 하기 때문)
추가
- ST(
Spanning Tree) =신장 트리
그래프에서모든 노드를 포함하면서사이클이 존재하지 않는부분 그래프
(모든노드 포함+사이클 X)
- MST(
Minmum Spanning Tree) =최소 신장 트리
최소한의 비용으로구성되는신장 트리- MST를 구하기 위한 알고리즘
- 크루스칼(
Kruskal) 알고리즘- 프림(
Prim) 알고리즘
- 그래프에서 순환(
Cycle) 판단 방법
- 무방향 그래프 -->
서로소 집합사용
Union-Find사용해서 판별 가능- 방향 그래프 -->
DFS활용
모든 정점에 대해DFS를 수행하는 방법 :O(V(V+E))소요방문 노드를 기록하고재방문일 경우Cycle로 판단하는 방법 :O(V)소요
-->재귀로 DFS수행, 각 재귀마다방문 노드를 기록하며재방문이 생기면Cycle로 판단
트리(Tree)
ref :
https://zorba91.tistory.com/293
https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-B-Plus-Tree
정점(V)과간선(E)를 이용해사이클을 이루지 않도록 구성한 Graph의 특수한 형태의 자료구조루트노드/부모노드/자식노드라는관계가 형성- 종류
- 이진 트리(Binary Tree)
:각 노드가최대 두개의 자식을 갖는트리- 이진 탐색 트리(Binary Search Tree)
:이진 트리를 기반하여 반드시좌측에 위치한 노드가우측에 위치한 노드보다작은 값을 가지는 규칙이 있는트리
- 이진 탐색 트리 검사 알고리즘
-->노드를 중심으로왼쪽 서브 트리의 최대값이 더작고,오른쪽 서브 트리의 최소값이 더큰지재귀로 확인이진 탐색 트리의 경우편향되어값이 들어가면 최대O(N)이 소요된다
-->AVL Tree/Red-Black Tree의 등장 원인- 균형 트리
:O(logN)시간에insert / find를 할 수 있을 정도로균형이 잘 잡혀있는 트리-->레드-블랙 트리/AVL트리- 등등 많은 트리 존재
AVL Tree
- AVL Tree
- 균형을 맞추는 방법
:왼쪽 / 오른쪽 서브트리의높이 차이가2이상일 때회전을 통해서트리의 높이를균형있게 맞춤- 특징
Red-Black 트리와시간복잡도는 같으나,삽입/삭제시회전이 더 자주 발생Red-Black 트리보다검색이효율적
Red-Black Tree
- Red-Black Tree
- 균형을 맞추는 방법
- ReColoring :
조건에 맞춰Red/Black으로재 색설정- ReStructuring :
조건에 맞춰적절한 회전으로균형을 조절- 특징
이진 탐색 트리중가장 효율적인 자료구조AVL-Tree보다삽입/삭제 연산이효율적AVL-Tree보다검색이비효율적
B-Tree
(
모든 키 값에데이터도함께 존재/편의상 생략된 것)
- 설명
이진 트리를확장해하나의 노드가가질 수 있는 자식 노드의 최대 숫자가2보다 큰 트리 구조최대 M개의 자식을 가질 수 있는 B트리를M차 B트리라고 함- 내부적으로
다양한 트리 구성 조건을 통해,트리의 균형을 맞추는 로직이존재함최악의 경우에도O(logN)의검색 성능을 보장검색은 기존이진 탐색 트리와동일한 방식으로 수행다양한 삽입과정은 다음 글 참조 --> 그림으로 알아보는 B-Tree
- B-Tree 구성 조건
- 노드는
최대 M개 부터 M/2개 까지의 자식을 가질 수 있습니다- 노드에는
최대 M−1개 부터 [M/2]−1개의 키가포함될 수 있습니다- 노드의
키가 x개라면자식의 수는 x+1개입니다최소차수는 자식수의 하한값을 의미하며,최소차수가 t라면 M=2t−1을 만족합니다 (최소차수 t가 2라면3차 B트리이며,key의 하한은 1개입니다)
B+Tree
- 설명
B-Tree와유사하지만리프노드(자식 노드가 없는 노드)가연결리스트 형태로 연결되어선형 검색이 가능한 트리- 모든
key,data가리프노드에 모여있으며,연결리스트로 연결된 구조 -->순차 처리 가능- B+ 트리는
인덱스구조에서순차접근에 대한 문제의 해결책으로제시- B+ 트리의
비단말 노드(index set)들은데이터의 빠른 접근을 위한인덱스 역할만 하기 때문에키와 포인터로만 구성실제 DB의 인덱스을구성하는자료 구조
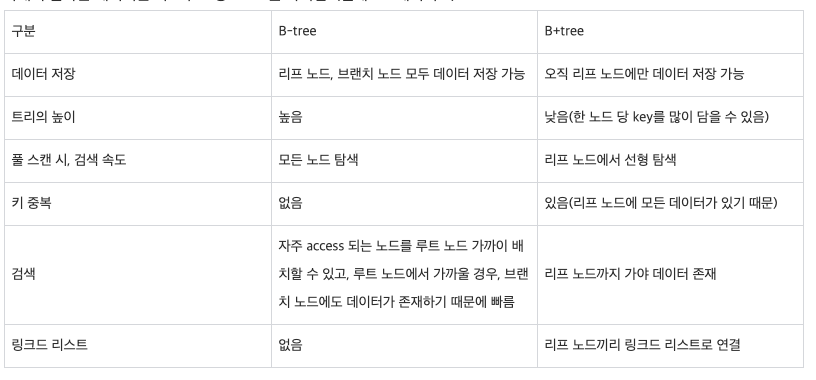
B-Tree 와 B+Tree 차이점
- 정리
B+Tree는leaf node끼리 연결리스트로 연결되어 있다B-Tree의각 노드에서는key뿐만 아니라,data도들어갈 수 있지만,B+Tree에서는순차 집합(leaf node의 집합)에만데이터가 들어갈 수 있음B+Tree는B-Tree와 달리삽입/삭제 연산이leaf node에서만 이루어짐
- 표
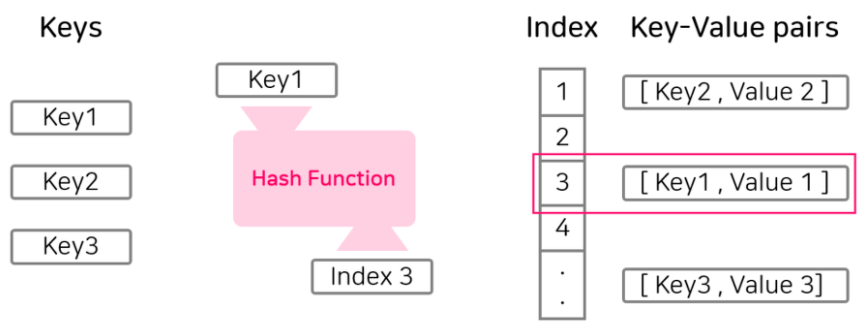
해시 테이블(Hash Table)
데이터를효율적으로 관리하기 위해,임의의 길이 데이터를고정된 길이의 데이터로매핑하는 것key와value를한 쌍으로저장하는 자료구조key를Hash함수로 연산하여나온 결과(해시값, 해시주소)으로Value를 찾는 방식을 사용key를이용하여Value를 빠르게 검색-->O(1)저장 공간을많이 필요로 한다 -->공간과탐색시간을맞바꾼 기법결국 데이터가 많아지면충돌(collision)이발생한다
- 그래도 해시 테이블을 쓰는 이유?
적은 자원으로많은 데이터를효율적으로 관리하기 위해무한한 데이터들을유한한 개수의 해시값으로매핑하면작은 메모리로 관리 가능인덱스 값을 통한 조회로평균 O(1)이 소요되지만,해시 index값이 충돌할 경우최대 O(n)이 소요
충돌 문제 해결
- 체이닝(Chaining)
연결리스트로노드를계속 계속 추가해 나가는 방식
-->제한 없이 계속 가능하나,메모리 문제가 발생- 개방 주소화(Open Addressing)
해시 함수로 얻은 주소가 아닌다른 주소에데이터를 저장할 수 있도록 허용 (해당 키 값에 저장되어있으면다른 주소에저장)개방 주소화 방식으로다른 주소를선택하는 방법들이 있다
선형 탐색: 정해진고정 폭으로 옮기는 방법2차원 탐색: 선형 탐사가 n칸 옆을 검사한다면, 이것은n^2칸 옆을 검사중복 해싱(이중 해싱):두번째 해시함수를 사용하여재 해싱
좋은 해시 함수란?
충돌 문제를해결하면서단순 균등 해싱에가깝도록 하는 것이체이닝이든,개방 주소화 방식이든해시테이블의 성능을 높이는데 중요균등한 확률(equally likely)로,독립적(idependently)으로해시되는 것이좋은해시 함수
주민번호처럼 특정한 패턴을 가지는값도되도록 불규칙적으로 만들어야 함
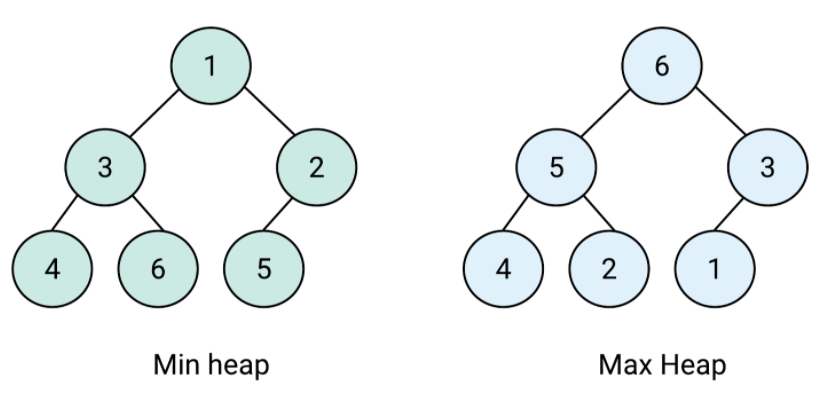
힙(Heap)
트리구조를기반으로 한자료구조로,데이터에서최대값과최소값을빠르게 찾기 위해 고안된완전이진트리(Complete Binary Tree)우선순위 큐(Priority queue)를구현하기 위한 자료구조힙의 루트노드에최대값이 있는 경우 -->최대힙(Max Heap)힙의 루트노드에 최소값이 있는 경우 -->최소힙(Min Heap)- Heapify 연산
Heap구조를 만들기 위한 연산O(logN)의시간복잡도소요
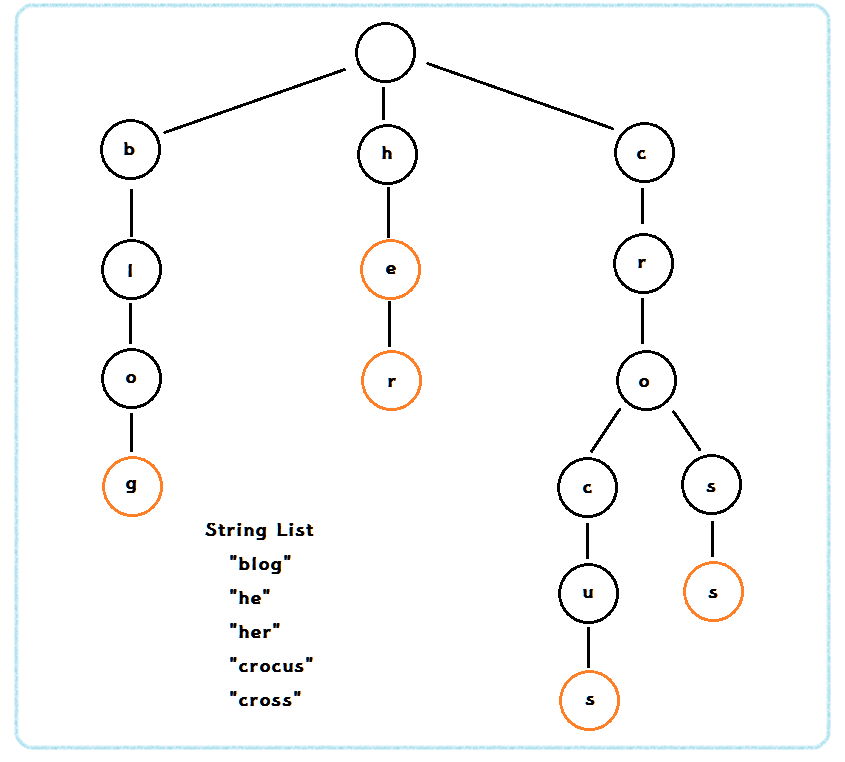
트라이(trie)
ref : https://www.crocus.co.kr/1053
문자열을저장하고효율적으로 탐색하기 위한트리 형태의자료구조문자열 하나를 찾는 데에는O(M)의시간복잡도로 해결 가능
-->BST(이진탐색트리)였으면문자열의 경우O(M*logN)소요 /M=문자열 최대 길이