Python start
- 운영체제별 차이점
| Windows | Linux | Mac OS | |
|---|---|---|---|
| 장점 | 친숙함, 초기엔 쉬움 | 모듈 설치 쉬움, 무료, 참고문서 많음 | 모듈 설치 쉬움, 참고문서도 많음 |
| 단점 | 모듈 설치 어려움 | OS 자체 사용이 어려움 | 비쌈 |
-
변수란?
프로그래밍에서 변수는 값을 저장하는 장소
변수는 메모리 주소를 가지고 있으며 변수에 들어가는 값은 메모리 주소에 할당 됨 -
폰 노이만 아키텍처
폰 노이만 아키텍처에서는 사용자가 컴퓨터에 값을 입력하거나 프로그램을
실행할 경우 그 정보를 먼저 메모리에 저장시키고 CPU가 순차적으로 그 정보를
해석하고 계산하여 사용자에게 결과값을 전달 -
컴퓨터의 반올림 오차
>>> c = 38.8
>>> print(c)
38.8
>>> c
38.799999999999999997단순한 실수도 이진수(반도체를 사용하기 때문)로 변환하면 무한소수가 됨
일반적으로 반올림 오차는 충분히 작아 문제가 되지 않는다.
-
Parameter VS Argument
- Parameter : 함수의 입력 값 인터페이스
- Argument : 실제 Parameter에 대입된 값
-
문자열 함수
>>> a.capitalize() # 첫 문자를 대문자로 변환- raw string
특수 문자 기호인 \ escape 글자를 무시하고 그대로 출력
>>> raw_string = r"파이썬 재밌어 \n 정말"
>>> print(raw_string)
파이썬 재밌어 \n 정말- function type hints
파이썬의 가장 큰 특징인 dynamic typing의 단점을 보완
PEP 484에 기반하여 type hints 기능 제공
def type_hint_example(name:str) -> str:
return f"Hello,{name}"- function docstring
- 파이썬 함수에 대한 상세 스펙을 사전에 작성
- 세개의 따옴표로 docstring 영역 표시(함수명 아래)
def kos_root():
'''
Return the path name of the ...
example
'''
global _kos_root
if _kos_root: return _kos_root
...- OrderedDict
- Dict와 달리, 데이터를 입력한 순서대로 dict를 반환함
- 그러나 dict도 python 3.6 부터 입력한 순서를 보장하여 출력
- Dict type 값을, value 혹은 key 값으로 정렬할 때 사용 가능
for k,v in OrderedDict(sorted(d.items(),key = lambda t: t[0])).items(): print(k,v) - namedtuple
- Tuple 형태로 Data 구조체를 저장하는 방법
- 저장되는 data의 variable을 사전에 지정해서 저장함
from collections import namedtuple as nt
Point = nt('Point',['x','y'])
p = Point(11,22)
>>> print(p[0] + p[1])
33- exception의 종류
| Exception 이름 | 내용 |
|---|---|
| IndexError | List의 index 범위를 넘어갈 때 |
| NameError | 존재하지 않은 변수를 호출 할 때 |
| ZeroDivisionError | 0으로 숫자를 나눌 때 |
| ValueError | 변환할 수 없는 문자/숫자를 변환할 때 |
| FileNotFoundError | 존재하지 않는 파일을 호출할 때 |
예시
for i in range(10):
try:
result = 10/i
except ZeroDivisionError as e:
print(e)
print("Not divided by 0")
else:
print(result)finally 구문 예시
try:
for i in range(1,10):
result = 10 // i
print(result)
except ZeroDivisionError:
print("Not divided by 0")
finally:
print("종료되었습니다.")필요에 따라 강제로 Exception을 발생
raise 구문 예시
while True:
value = input("변환할 정수 값을 입력해주세요")
for digit in value:
if digit not in "0123456789":
raise ValueError("숫자값을 입력하지 않으셨습니다.")
print("정수값으로 변환된 숫자 -",int(value))특정 조건에 만족하지 않을 경우 예외 발생
assert 구문 예시
def get_binary_number(decimal_number):
assert isinstance(decimal_number,int)
return bin(decimal_number)
print(get_binary_number(10)) -
Logging Handling
- logging 모듈
python의 기본 Log관리 모듈
import logging logging.debug("틀렸잖아") logging.info("확인해") logging.warning("조심해") logging.error("에러났어") logging.critical("망했다")-
logging level
- 프로그램 진행 상황에 따른 다른 Level의 Log를 출력함
- 개발 시점, 운영 시점 마다 다른 Log가 남을 수 있도록 지원함
- DEBUG > INFO > WARNING > ERROR > Critical
- Log 관리시 가장 기본이 되는 설정 정보
Level 개요 예시 debug 개발시 처리 기록을 남겨야하는 로그 정보를 남김 다음 함수로 A를 호출함, 변수 A를 무엇으로 변경함 info 처리가 진행되는 동안의 정보를 알림 서버가 시작되었음, 서버가 종료됨, 사용자 A가 프로그램에 접속함 warning 사용자가 잘못 입력한 정보나 처리는 가능하나 원래 개발시 의도치 않는 정보가 들어왔을 때 알림 Str입력을 기대했으나 int가 입력됨 (Str casting으로 처리함) error 잘못된 처리로 인해 에러가 났으나, 프로그램은 동작할 수 있음을 알림 파일에 기록을 해야하는데 파일이 없음 (Exception 처리 후 사용자에게 알림) critical 잘못된 처리로 데이터 손실이나 더이상 프로그램이 동작할 수 없음을 알림 잘못된 접근으로 해당 파일이 삭제됨, 사용자의 의한 강제 종료 import logging logger = logging.getLogger("main") stream_hander = logging.StreamHandler()
- logging 모듈
-
numpy
array shape : array의 RANK에 따라 불리는 이름이 있다.
Rank Name Example 0 scalar 7 1 vector [10,10] 2 matrix [[10,10],[15,15]] 3~n tensor [[[1,5,9],[2,6,10]],[[3,7,8],[4,8,12]]] reshape : Array의 shape의 크기를 변경함,element의 갯수는 동일
>>> test_matrix = [[1,2,3,4],[1,2,5,8]] >>> np.array(test_matrix).shape (2,4) >>> np.array(test_matrix).reshape(8,) array([1,2,3,4,1,2,5,8])flatten : 다차원 array를 1차원 array로 변환 ( reshape(-1)와 같음 )
>>> test_matrix = [[1,2,3,4],[1,2,5,8]] >>> np.array(test_matrix).flatten() array([1,2,3,4,1,2,5,8])arrange : array의 범위를 지정하여, 값의 list를 생성하는 명령어
np.arrange(30) np.arrange(0,5,0.5) np.arrange(30).reshape(5,6)zeros : 0으로 가득찬 ndarray 생성
ones : 1로 가득찬 ndarray 생성# zeros np.zeros(shape=(10,),dtype=np.int8) np.zeros((2,5)) # ones np.ones(shape=(10,),dtype=np.int8) np.ones((2,5))something_like : 기존 ndarray의 shape 크기 만큼 1,0 또는 empty array를 반
test_matrix = np.arange(30).reshape(5,6) np.ones_like(test_matrix) # 1으로 가득찬 np.zeros_like(test_matrix) # 0으로 가득찬identity : 단위 행렬을 생성함
>>> np.identity(n=3,dtype=np.int8) array([[1,0,0], [0,1,0], [0,0,1]], dtype=int8)eye : 대각선이 1인 행렬, k값의 시작 index의 변경이 가능
>>> np.eye(3) array([[1.,0.,0.], [0.,1.,0.], [0.,0.,1.]]) >>> np.eye(N=3,M=5, dtype=np.int8) array([[1,0,0,0,0], [0,1,0,0,0], [0,0,1,0,0]], dtype=int8) >>> np.eye(3,5,k=2, dtype=np.int8) array([[0,0,1,0,0], [0,0,0,1,0], [0,0,0,0,1]], dtype=int8)diag : 대각 행렬의 값을 추출함
>>> matrix = np.arange(9).reshape(3,3) array([[0,1,2], [3,4,5], [6,7,8]]) >>> np.diag(matrix) array([0,4,8]) >>> np.diag(matrix,k=1) # k : start_index array([1,5])random sampling : 데이터 분포에 따른 sampling으로 array를 생성
>>> np.random.uniform(0,1,10).reshape(2,5) #균등분포 >>> np.random.normal(0,1,10).reshape(2,5) # 정규분포
-
numpy array operations
Element-wise operations : array간 shape이 같을 때 일어나는 연산
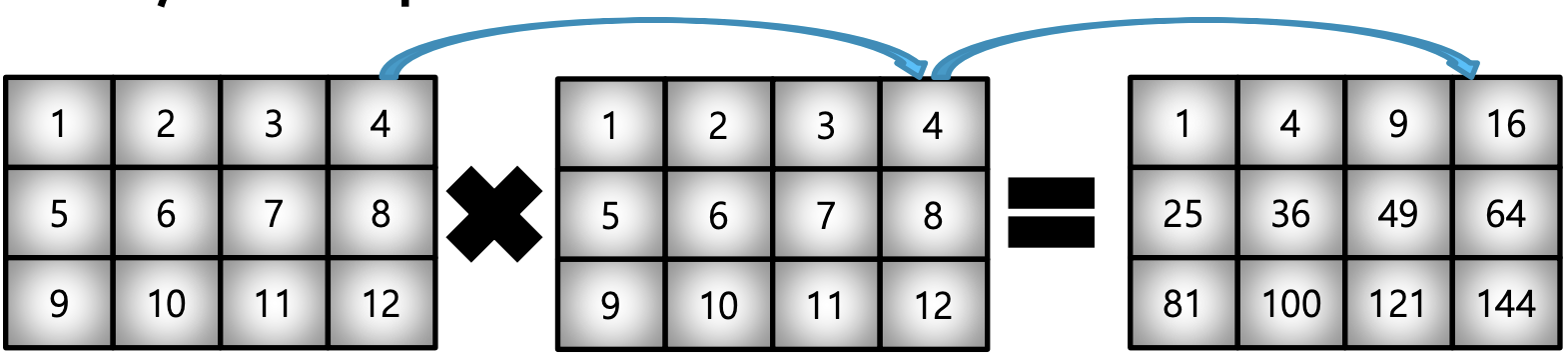
>>> matrix_a = np.arange(1,13).reshape(3,4) >>> matrix_a * matrix_aDot product : matrix의 기본 연산, dot 함수 사용
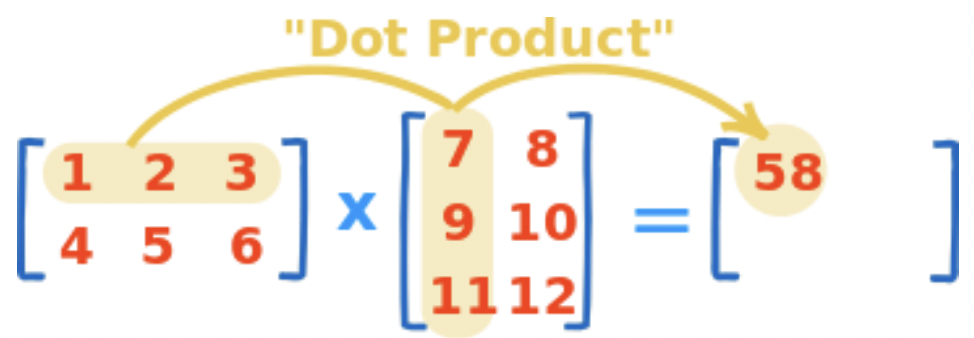
>>> test_a = np.arange(1,7).reshape(2,3) >>> test_b = np.arange(7,13).reshape(3,2) >>> test_a.dot(test_b) -
numpy comparisons
np.all : 모두가 조건에 만족한다면 True
np.any : 하나라도 조건에 만족한다면 True>>> a = arange(10) >>> np.any(a>5), np.any(a<0) (True, False) >>> np.all(a>5), np.all(a<10) (False,True)np.where
>>> a = np.array([1,3,0]) >>> np.where(a > 0, 3, 2) #where(condition,True,False) array([3,3,2]) >>> np.arange(10) >>> np.where(a>5) #Index 값 반환 array([6,7,8,9])
fancy index : numpy는 array를 index value로 사용해서 값 추출
>>> a = np.array([2,4,6,8], float)
>>> b = np.array([0,0,1,3,2,1], int) #반드시 integer로 선언
>>> a[b] #bracket index, b 배열의 값을 index로 하여 a의 값을 추출
array([2., 2., 4., 8., 6., 4.])
>>> a.take(b) #take 함수: bracket index와 같은 효과- map for series
>>> df.sex.unique()
array(['male', 'female'], dtype = object)
>>> df.sex.map({"male" : 0, "female" : 1})- replace function
- Map 함수의 기능 중 데이터 변환 기능만 담당
- 데이터 변환시 많이 사용되는 함수
>>> df.sex.replace({"male":0,"female":1}) >>> df.sex.replace(["male","female"],[0,1],inplace=True) - Groupby
- SQL groupby 명령어와 같다.
- split -> apply -> combine 과정을 거쳐 연산한다.
#적용받는 컬럼 >>> df.groupby("Team")["Points"].sum() #묶음의 기준 #적용받는 연산 >>> df.groupby(["Team","Year"])["Points"].sum() #한 개이상의 컬럼을 묶을 수 있음- Hierarchical index : 여러개의 column으로 groupby를 할 경우
- unstack() : group으로 묶여진 데이터를 matrix형태로 전환해줌
>>> h_index.unstack()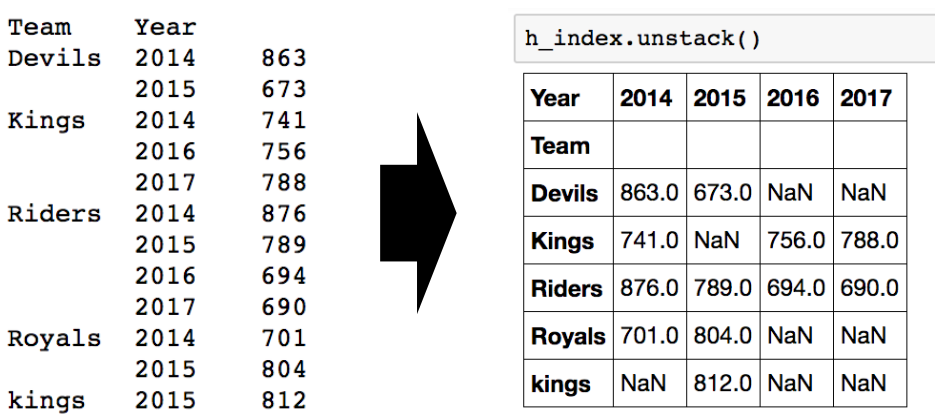
- swaplevel : index level을 변경 가능
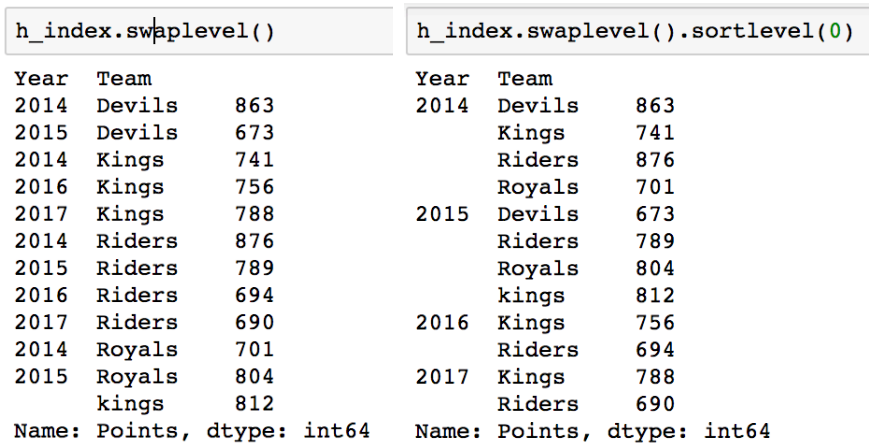
- index level을 기준으로 연산 가능
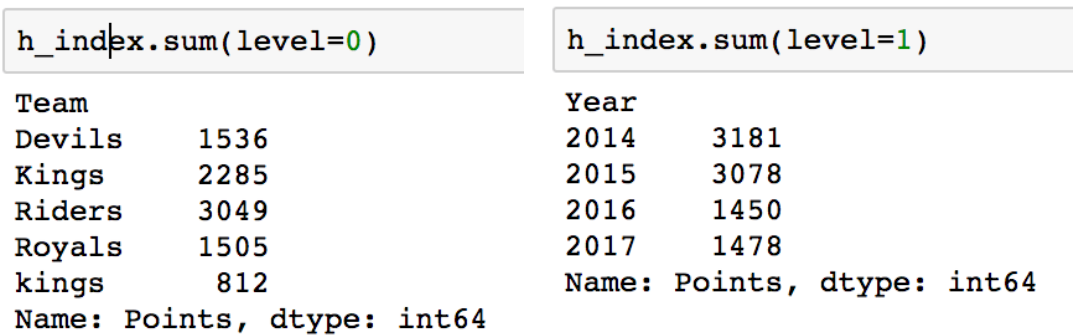
- unstack() : group으로 묶여진 데이터를 matrix형태로 전환해줌
Math
-
벡터
- 벡터는 숫자를 원소로 가지는 리스트 또는 배열이다.
- 벡터끼리 같은 모양을 가지면 성분곱(Hadamard product)을 계산할 수 있다.
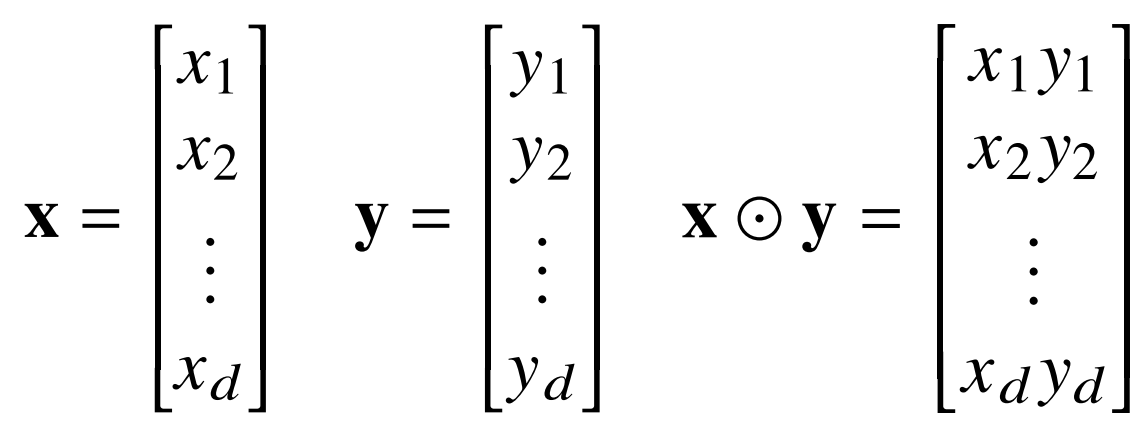
- 두 벡터의 덧셈은 다른 벡터로부터 상대적 위치이동을 표현합니다.
- 벡터의 노름은 원점에서부터의 거리를 말합니다.
- -노름은 각 성분의 변화량의 절대값을 모두 더합니다.
- -노름은 피타고라스 정리를 이용해 유클리드 거리를 계산합니다.
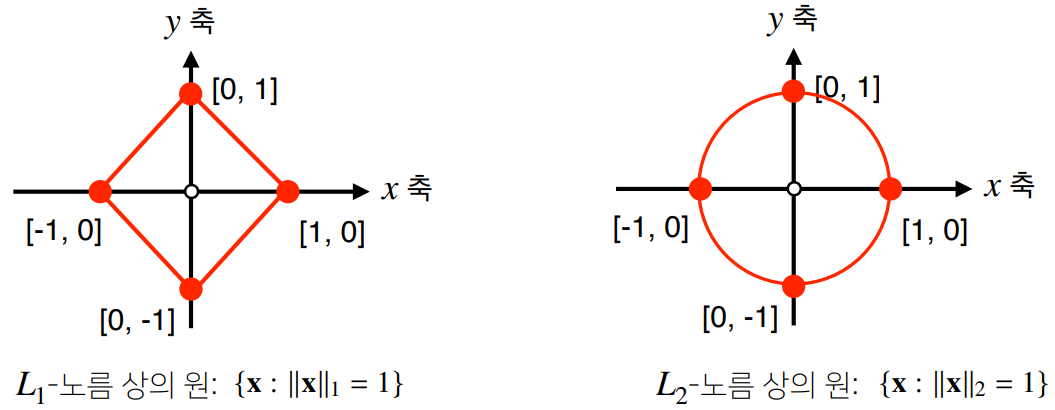
- 두 벡터 사이의 거리는 벡터의 뺄셈을 통해 계산할 수 있다.
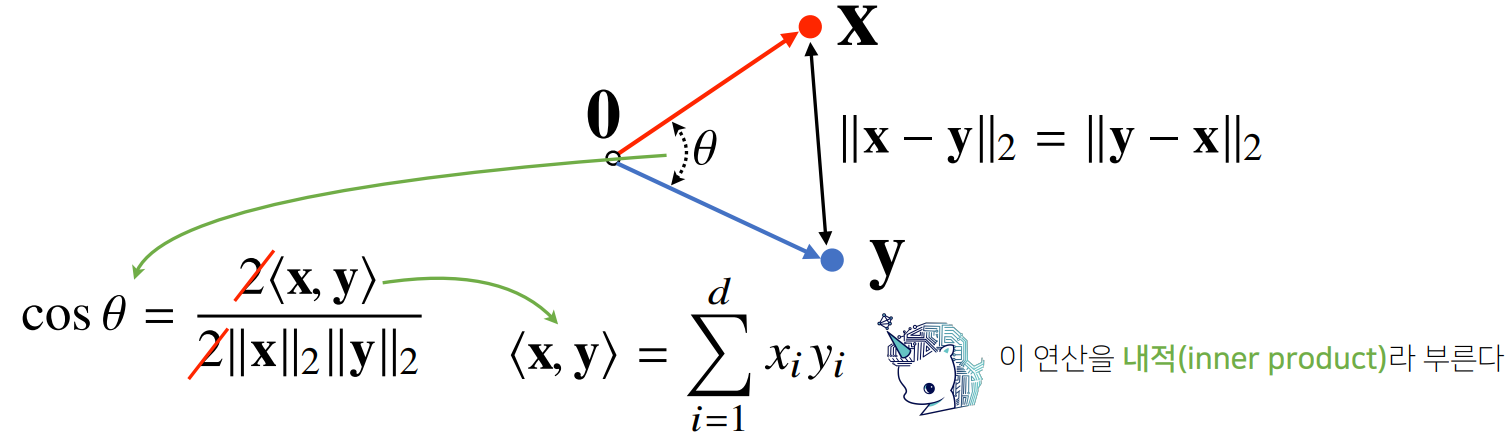
- 두 벡터 사이의 각도는 두 벡터 사이의 거리를 통해 계산할 수 있습니다.
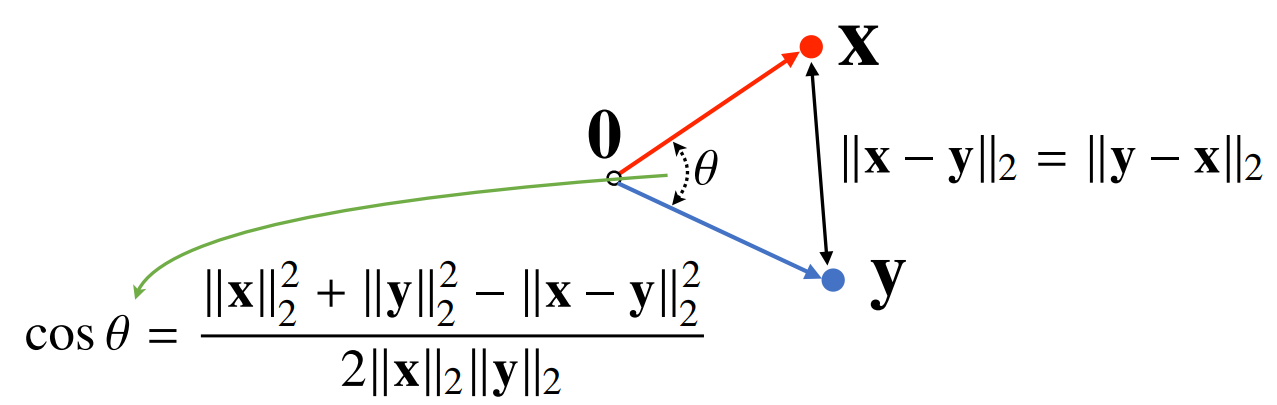 내적을 통해 분자를 쉽게 계산할 수 있습니다.
내적을 통해 분자를 쉽게 계산할 수 있습니다.
-
행렬
- 행렬 곱셈 : i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산
- numpy에서는
@연산을 사용한다. Ex :X @ Y
- 행렬 곱셈 : i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산
-
경사하강법
- 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해선 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장된다.
- 하지만 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있기에 수렴이 항상 보장되지 않는다.
- 그렇기에 볼록이 아닌 목적식은 SGD를 통해 최적화한다.
- SGD는 미니배치 를 가지고 그레디언트 벡터를 계산한다. 미니배치는 확률적으로 선택하므로 목적식 모양이 바뀌게 된다.
- SGD는 볼록이 아닌 목적식에도 사용 가능하므로 머신러닝에 학습에 보다 효율적이다.
-
확률론
- 딥러닝은 확률론 기반의 기계학습 이론에 기반을 두고 있다.
- 기계학습에서 사용되는 손실함수(Loss function)들의 작동 원리는 데이터 공간을 통계적으로 해석해서 유도하게 됩니다.
- 분산 및 불확실성을 최소화하기 위해서는 측정하는 방법을 알아야한다.
- 확률변수는 확률분포 에 따라
이산형과연속형확률변수로 구분 - 이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링한다.
- 는 확률변수 x 값을 가질 확률
- 연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density) 위에서의 적분을 통해 모델링한다.
- 몬테카를로 샘플링
- 기계학습의 많은 문제들은 확률분포를 명시적으로 모를 때가 대부분이다.
- 확률분포를 모를 때 데이터를 이용하여 기대값을 계산하려면 몬테카를로 샘플링 방법을 사용해야 한다. (이산형이든 연속형이든 상관없이 성립한다.)
- ,
- 독립추출만 보장된다면 대수의 법칙에 의해 수렴성을 보장한다.
-
통계학
-
통계적 모델링은 적절한 가정 위에서 확률분포를 추정하는 것이 목표
-
유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알 수 없으므로, 근사적으로 확률 분포를 추정한다.
-
데이터가 특정 확률분포를 따른다고 선험적으로(apriori) 가정한 후 그 분포를 결정하는 모수(parameter)를 추정하는 방법을 모수적(parametric) 방법론이라 합니다.
-
특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌면 비모수(nonparametric) 방법론이라부릅니다
-
확률분포 가정하기
- 데이터가 2개의 값(0또는 1)만 가지는 경우 : 베르누이 분포
- 데이터가 n개의 이산적인 값을 가지는 경우 : 카테고리 분포
- 데이터가 [0,1] 사이에서 값을 가지는 경우 : 베타 분포
- 데이터가 0 이상의 값을 가지는 경우 : 감마 분포, 로그정규 분포 등
- 데이터가 R 전체에서 값을 가지는 경우 : 정규 분포, 라플라스 분포 등
-
최대가능도 추정법
- 확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 달라지게 된다.
- 이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나는 최대가능도 추정법(maximum likelihood estimation, MLE)입니다.
-
확률분포의 거리
- 기계학습에서 사용되는 손실 함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도합니다.
- 데이터 공간에 두 개의 확률분포,가 있을 경우 확률분포 사이의 거리(distance)를 계산할 때 다음과 같은 함수들을 이용합니다
- 총변동 거리
- 쿨백-라이블러 발산
- 바슈타인 거리
- 쿨백-라이블러 발산(KL Divergence)
- 이산 :
- 연속 :
- 분리 : +
- 분리 : = 크로스 엔트로피 + 엔트로피
-
출처 : 네이버 부스트캠프
참고자료 : dive into deeplearning (한국어)
