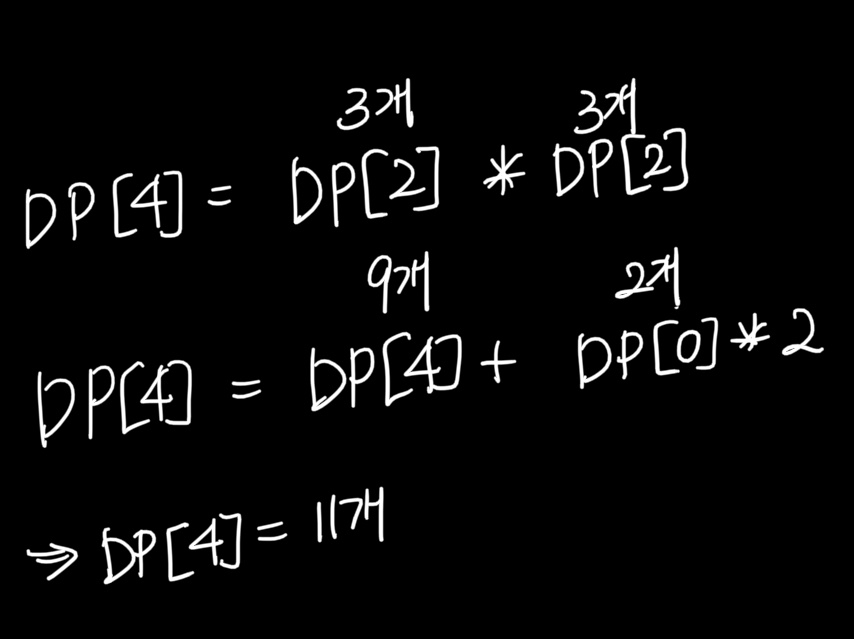[JAVA/2133번] 타일 채우기

고지훈·2021년 10월 9일

2133번 JAVA JAVA 알고리즘 백준 2133번 백준 2133번 자바 백준 타일채우기 JAVA 백준 타일채우기 자바 백준알고리즘 타일채우기 자바

Algorithm

목록 보기

35/68

문제

입력 및 출력

풀이


import java.io.*;

class Main {
    public static void main(String args[]) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));


        // N(1 <= N <= 30)
        int N = Integer.parseInt(br.readLine());

        // N은 1부터 시작하기 때문에 N + 1의 크기를 갖는 배열을 선언한다.
        int[] DP = new int[N + 1];


        // N이 홀수일 경우, 2x1 or 1x2의 타일로 채울 수 없기 때문에 0을 출력하고 return
        if (N % 2 != 0) {
            System.out.println(0);
            return;
        }

        // 타일이 없을 경우 2x1, or 1x2의 타일로 채울 수 있는 경우의 수는 아무것도 채우지 않는 경우이다
        DP[0] = 1;

        // 3x1 타일을 채울 수 있는 경우의 수는 0개이다.
        DP[1] = 0;

        // 3x2 타일을 채울 수 있는 경우의 수는 3개이다.
        DP[2] = 3;

        // N은 홀수가 될 수 없고 짝수만 될 수 있기 때문에 2씩 증가를 한다.
        for (int i = 4; i <= N; i += 2) {
            DP[i] = DP[i - 2] * DP[2];
            for (int j = i - 4; j >= 0; j -= 2) {
                DP[i] = DP[i] + (DP[j] * 2);
            }
        }

        // 결과값 출력
        System.out.println(DP[N]);
    }
}

결과 및 해결방법

[결과]

[정리]

해결방법
3xN 크기의 벽을 1x2와 2x1의 타일로만 채울 때, 경우의 수를 구해야 하는 문제이다.
DP[N] = R의 공식을 사용하여 표현해보자면, 3xN의 벽을 1x2, 2x1의 타일로만 채울 때, 채울 수 있는 경우의 수는 R개이다를 의미한다.

첫 번째로 N이 홀수일 경우를 생각해보자.
N이 1일 경우로 1x2, 2x1의 타일로만 채울 수 있는 경우의 수는 0개이다. 따라서 N이 홀수일 경우 0을 리턴시켜주어야 하는것을 확인할 수 있다.
=> N%2 != 0일 경우, 0을 리턴

두 번째로 N이 0일 경우를 생각해보자.
타일을 하나도 만들지 않을 경우, 1x2, 2x1 타일로만 채울 수 있는 경우의 수는 1개이다. 타일을 아무것도 놓지 않은 경우이기 때문이다.
=> DP[0] = 1

위의 두가지 경우로 N이 홀수와 0인 경우를 파악했으므로 이제부터 짝수인 경우를 판단해보자.

가장 먼저 N이 2인 경우를 생각해보자.
3x2의 벽을 1x2, 2x1타일로만 채워야 할 경우 나타낼 수 있는 경우의 수는 3가지이다.

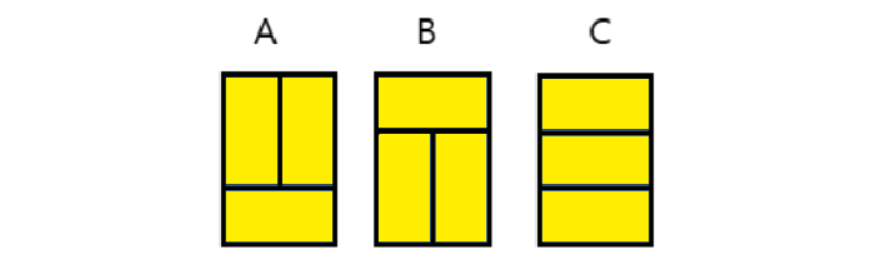
=> DP[2] = 3

다음으로 N이 4인 경우를 생각해보자.
3x4의 벽을 생각해보면 3x2의 벽을 두번 채우는 형태로 생각해볼 수 있다. 우리는 DP[2] = 3인 결과 값을 이미 알고 있다.
위의 3가지 형태를 조합해서 나타낼 경우 다음과 같이 9개의 경우의 수가 나온다.

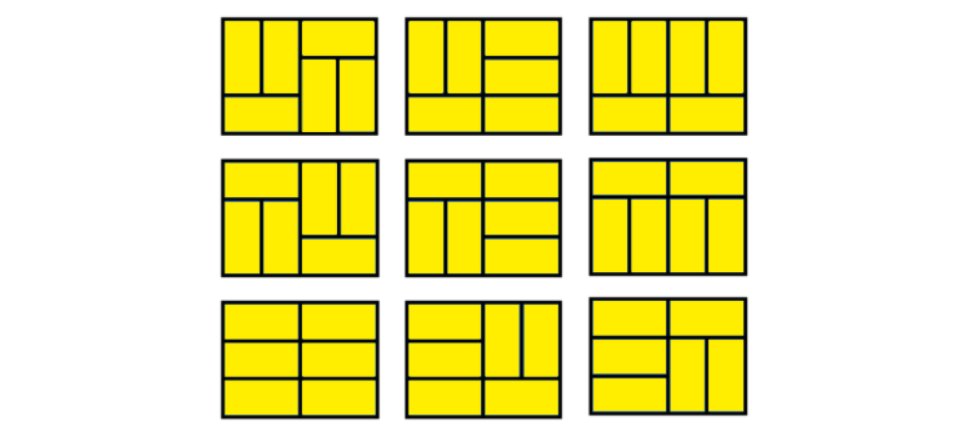
하지만 위의 예 이외에도 나눠지는 경우가 2가지 존재한다.

위 그림은 우리가 기존에 해결했던 방식인 3x2의 방법을 두번 수행한 방법으로 나타낼 수 없는 경우이다. 이로써 3x4의 경우부터 규칙이 있지 않은 패턴이 등장하게 된다.
=> DP[4] = 11

다음으로 N이 6인 경우를 생각해보자.
3x6의 벽을 나눌 수 있는 방법은 (3x2) x (3x4)의 경우의 수와 (3x4) x (3x2)의 경우의 수가 있을 것이다. 위의 공식대로 계산을 수행할 경우 33개 + 33개로 66개가 나올 것이다.

하지만 이와같이 계산할 경우, 중복되는 경우의 수가 많이 존재하기 때문에 정답이 될 수 없다.중복을 제거하기 위해서는 두번째 경우의 DP[4]에 DP[2]의 경우가 들어가면 안될 것이다. 따라서 두번째 DP[4]에는 규칙이 있지 않은 패턴을 넣어주어야 할 것이다.

따라서 DP[4] DP[2]가 33가지의 경우의 수이고 DP[2] 2가 6가지 경우의 수를 가질 것이다. 여기서 또한 3x4에서와 마찬가지로 특별한 모양을 갖는 경우의 수가 2가지 있기때문에 2를 더해야한다.

=> DP[6] = 41개