오늘 풀어본 문제는 BOJ 15685 드래곤 커브 이다!
시뮬레이션 문제이지만 규칙성을 찾기 너무 어려웠고 이런 유형은 또 처음인 것 같아서 공부가 많이 된 문제이다! 얼마든지 나올 수 있을 것 같아 시간이 지난 뒤 꼭 다시 풀어봐야겠다!
BOJ 15685 드래곤 커브
드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다. 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
- 시작 점 2. 시작 방향 3. 세대
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.
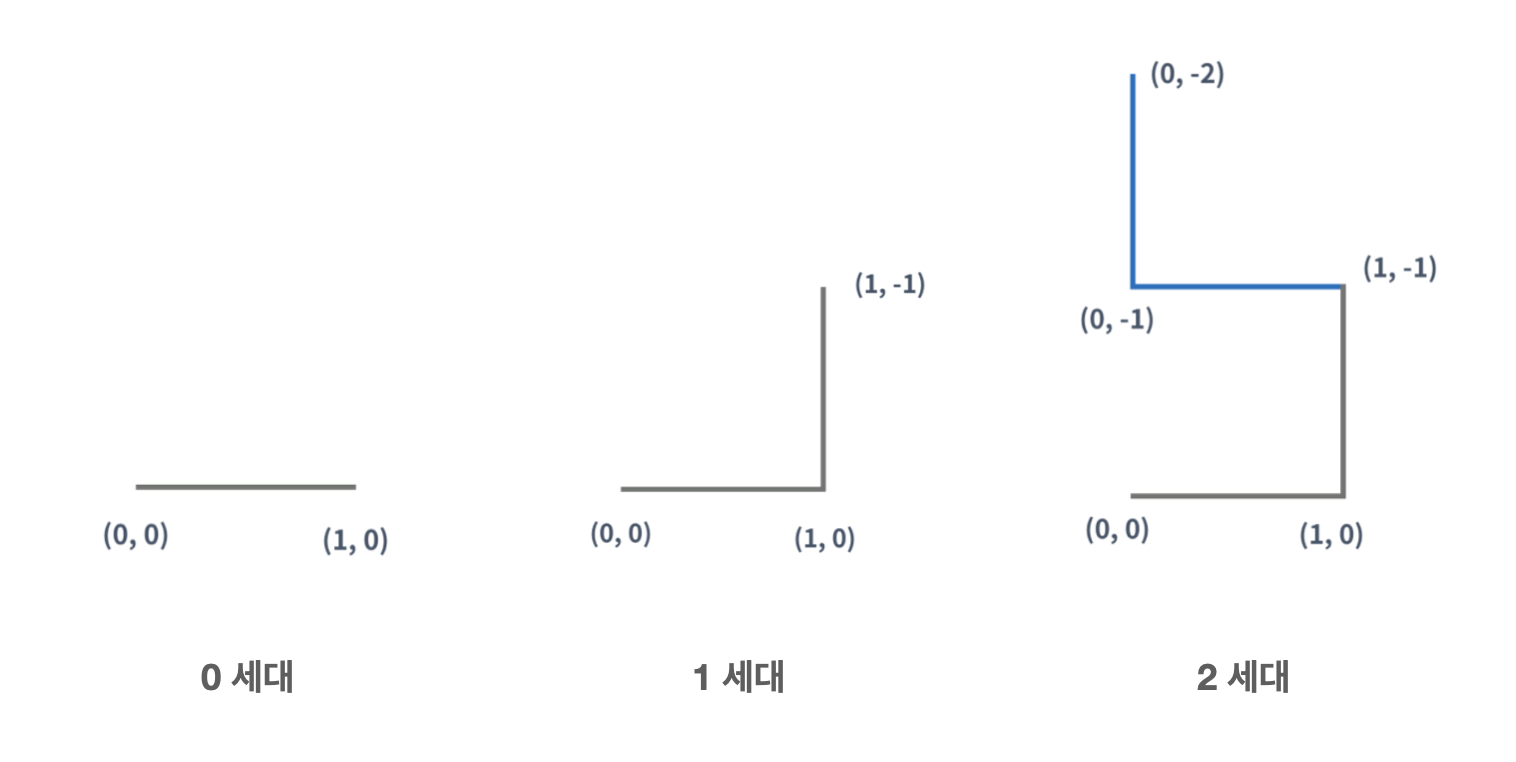
1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.
2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)

3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.
즉, K(K > 1)세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점에 붙인 것이다.
크기가 100×100인 격자 위에 드래곤 커브가 N개 있다. 이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오. 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.
입출력
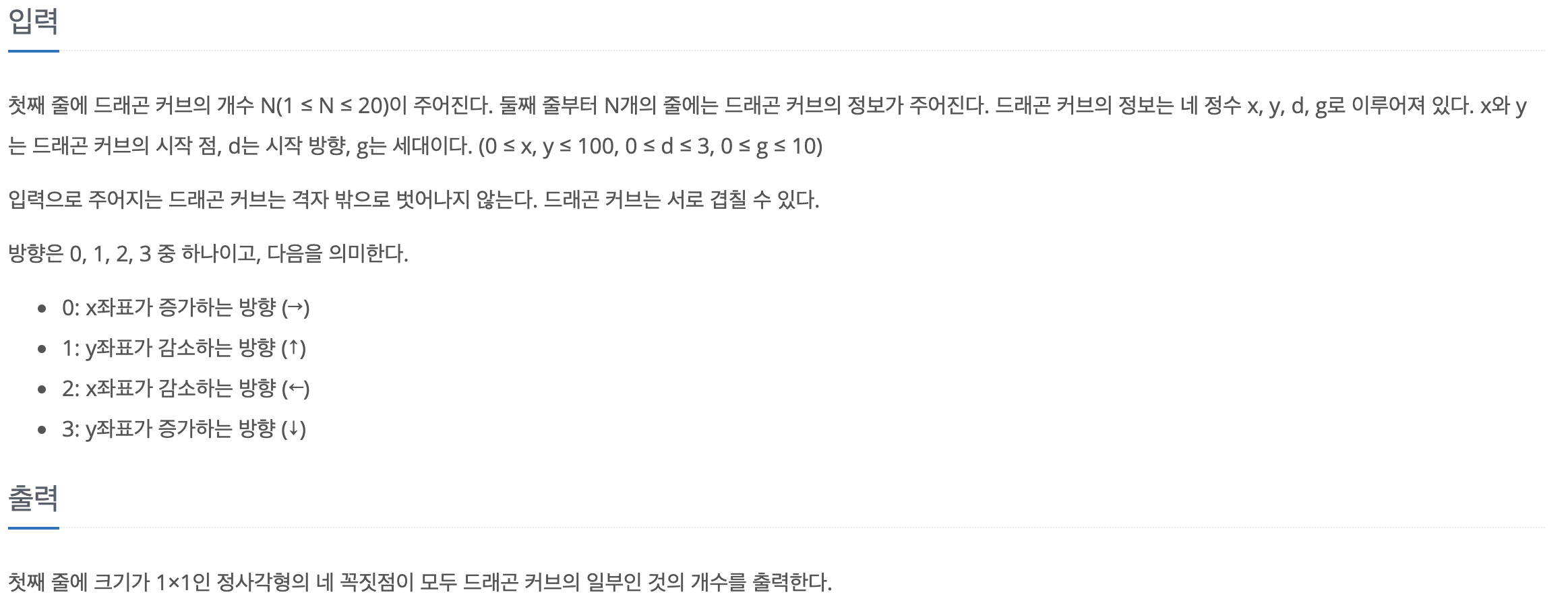
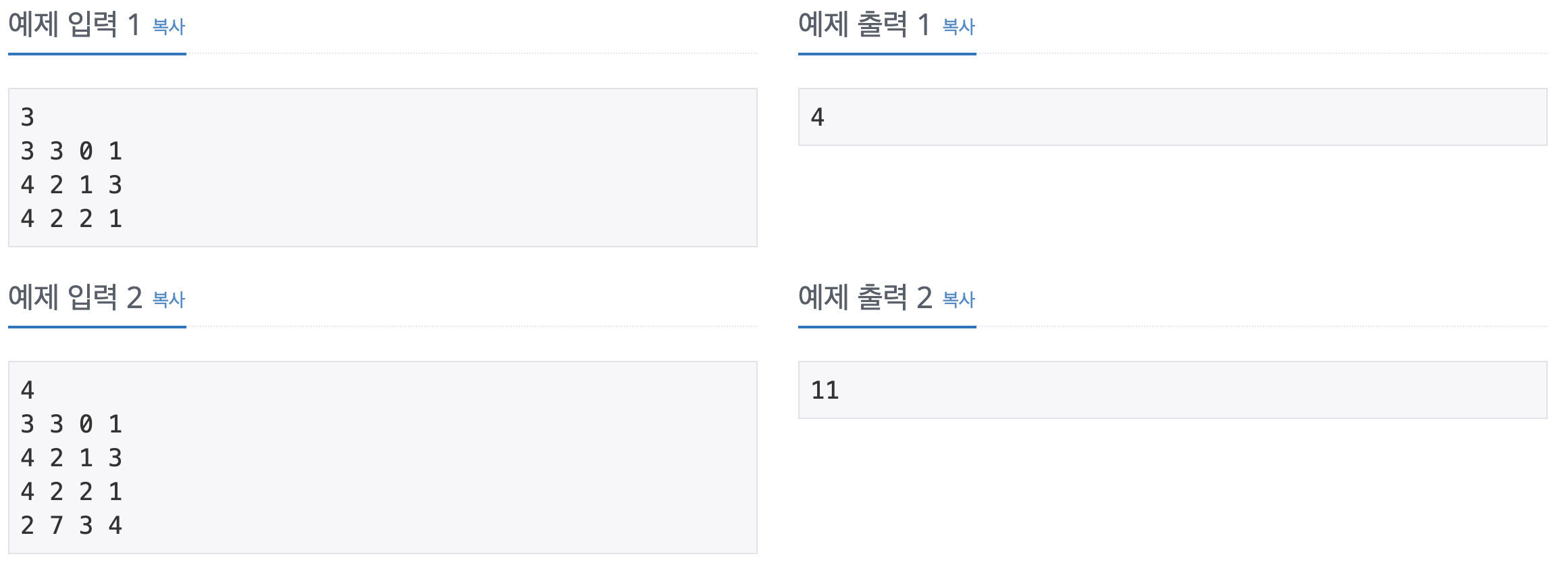
나의 풀이
일단 문제 자체를 이해하는데 조금 시간이 걸렸다..ㅋㅋㅋㅋ
이게 뭔 소리여.. 하면서 풀었던,,
현실적으로 내 머리로 모든 경우의 수를 파악할 수 없으니 분명 무슨 규칙이 있겠지 머~ 해서 규칙을 찾으려고 찾으려고,,, 그림을 그리고,, cos,, tan,, 온갖거를 다 가져다 그려보고 써봤지만 결론적으로 난 찾지 못했다 ^^ 규..칙.. 성... ㅜ
나는 점들이 움직이는 것의 규칙성을 찾으려 했다. (x1, y1) -> (x2, y2) 의 점의 변화에 있어서 변화량의 규칙이 있지 않을까 생각했는데 답은 그게 아니었다!
여러 좌표들의 변화가 아니라 좌표는 오직 시작 점 하나만을 기준으로 하고 방향의 변화에 있어서 규칙성을 파악하는 것이 핵심이었다!
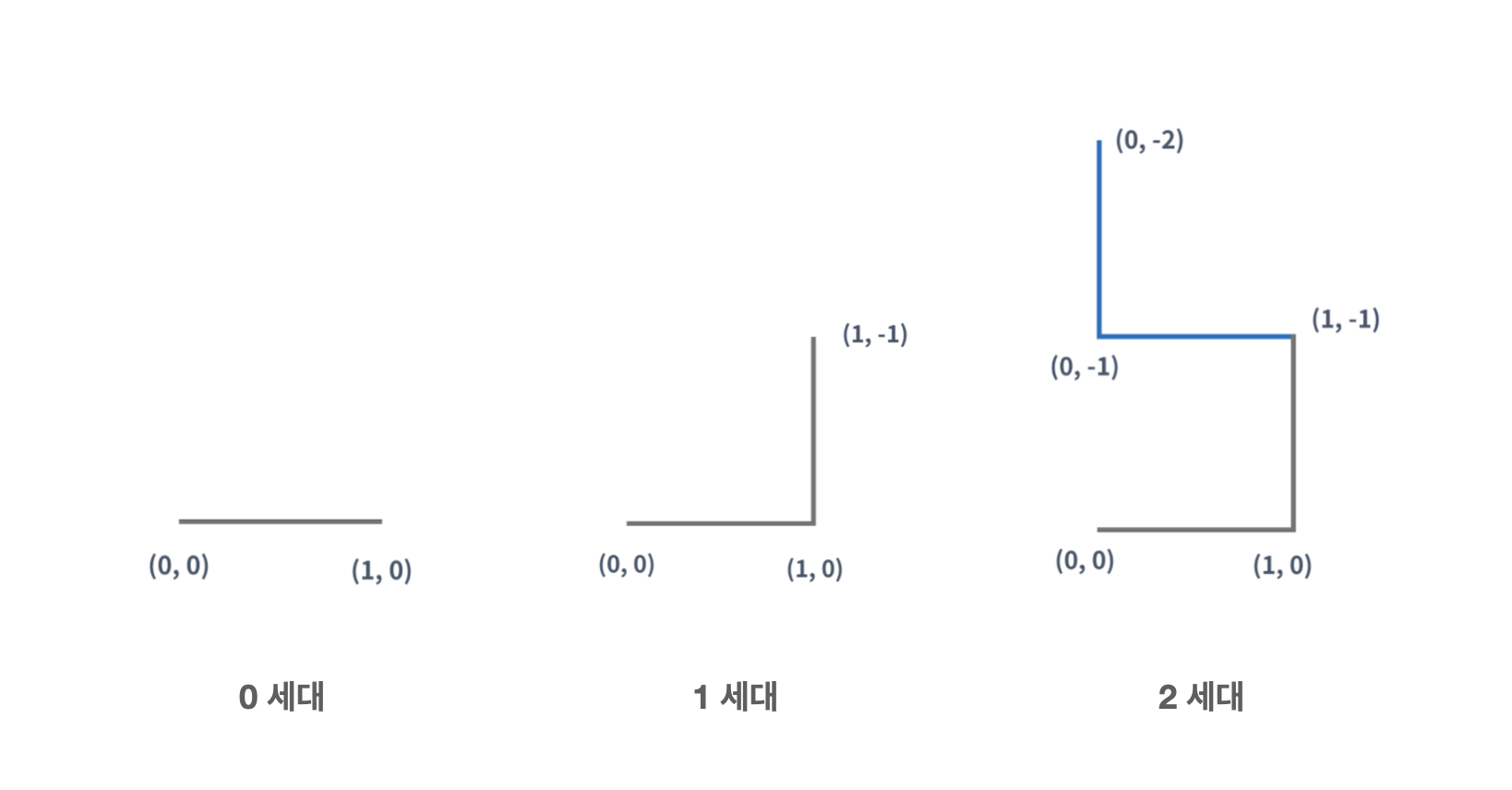
처음에 주어지는 방향 번호가 0이라고 가정 하면,
시작점 (0,0) 에서 0방향(->) 으로 움직인 곳이 끝점 (1,0) 이 되어 0세대 선분이 완성된다.
이후 선분을 다시 끝점 (1,0)을 기준으로 시계방향 90도 회전시켜 닿는 곳이 새로운 끝점 (1,-1) 이 되는데 이때 끝점이 이동하는 방향 (1,0)->(1,-1)을 보면 방향1 (↑)과 일치 한다.
점이 이동하는 방향만을 본다면 2세대 선분은 방향 전환 순서는 0(→) - 1(↑) - 2(←) - 1(↑) 와 같다.
- 0세대 : 0
- 1세대 : 0 - 1
- 2세대 : 0 - 1 - 2 - 1
이때, 2세대 에서 추가된 마지막 2개 선분의 방향 (2-1)을 보면 1세대 선분(0-1)을 역순으로 하여 1을 더한 값이라는 걸 알 수 있다.
2세대 : 0 - 1 - 2(1+1) - 1(0+1).
즉, k 세대에서 새롭게 추가되는 선분의 방향은 k-1 세대의 선분 방향을 역순으로 하여 1을 추가한 것이다!
이 규칙성을 찾는 것이 이 문제의 핵심이겠다!!
규칙성을 찾은 뒤론 코드로 구현하는 것만 남아있다.
- 선분의 마지막 좌표
<pair<int, int>>> last - 선분의 방향을 기록한 배열
vector<int> directions - k 세대에서 새로운 선분 추가 시 이전까지 기록된 directions 를 기반으로 directions.size() 만큼 새로운 방향을 추가하고 새롭게 추가된 directions 대로 last 좌표를 이동시키면서 map[last.first][last.second] = 1 로 수정
- 모든 선분을 그린 뒤 map 에서 인접해있는 4칸이 모두 1인 경우 count
코드
#include <iostream>
#include <vector>
// BOJ 15685 드레곤 커브, simulation
using namespace std;
int dy[4] = {0,-1,0,1};
int dx[4] = {1,0,-1,0};;
vector<vector<int>> map(101, vector<int>(101, 0));
void drawDragonCurve(int x, int y, int dir, int gen){
vector<int> directions;
directions.push_back(dir);
pair<int, int> last = make_pair(y+dy[dir], x+dx[dir]);
map[y][x] = 1;
map[last.first][last.second] = 1;
while (gen > 0){
int size = directions.size();
for (int i = size-1; i >= 0; i--) { // 새로운 방향 추가
directions.push_back((directions[i]+1)%4);
}
for (int i = size; i < 2*size; ++i) { // 추가된 방향 만큼 선분 연장
last.first += dy[directions[i]];
last.second += dx[directions[i]];
map[last.first][last.second] = 1;
}
gen--;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N, x, y, dir, gen;
cin>>N;
for (int i = 0; i < N; ++i) {
cin>>x>>y>>dir>>gen;
drawDragonCurve(x, y, dir, gen);
}
int box = 0;
for (int i = 0; i < 100; ++i) {
for (int j = 0; j < 100; ++j) {
if (map[i][j]==1){
if (map[i][j+1]==1 && map[i+1][j] && map[i+1][j+1]) box++;
}
}
}
cout<<box;
return 0;
}