[알고리즘 풀이 분석] BOJ 9251 LCS

오늘부터 가능하면 2개이상 문제를 풀어보고자 한다!
오늘 두번째로 풀어본 문제는 BOJ 9251 LCS 이다!
DP 문제이고, LCS 라는 개념을 새롭게 알게 되었는데 기억할 필요가 있을 것 같다!!

BOJ 9251 LCS

LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.

예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.

입출력

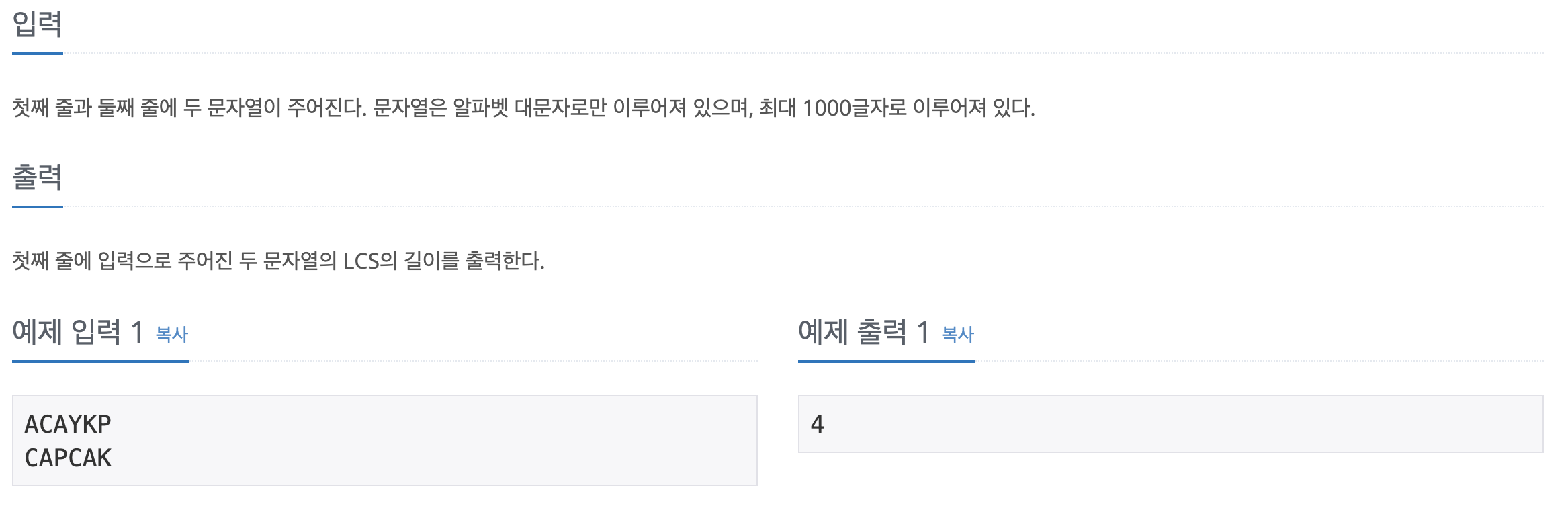
나의 풀이 & LCS 알고리즘

일단은 문제를 읽었을 때 LCS 라는 개념 자체가 조금 생소했다. 수열인데 저허게 떨어진 부분까지 같은 수열이라고 해도 되는건가,,? 싶고,,

이문제를 어떻게 DP로 풀까 이리저리 고민을 많이 했다.
일단은 예제를 보자니 주어진 문자열을 앞에서 뒤 방향으로 탐색하는 것이 맞는 것 같은데, 일일이 대조하자니 시간초과가 분명 날 것 같았다.

결국, LCS (Longest Common Subsequence) 의 개념을 찾아보았고 DP를 사용해 굉장히 간단하게 해결할 수 있었다.

Subsequence

subsequence 라는 것의 개념을 간단하게 잡고가자!

subsequence?
subsequence는 s 라는 sequence가 있을 때 s의 subsequence는 s의 일부 요소들을 원래의 순서를 지키면서 순서대로 나열해 얻을 수 있는 수열을 말한다!

문자열 s = "hello world" 를 예로 들었을 때 s의 subsequence는 "h", "hello" 는 물론 "hwd", "wld", "hlorld" 등도 가능한 것이다!

우리는 주어지는 두 string 의 모든 subsequence 들 중에서 공통으로 해당되고, 그 중 가장 긴 것의 길이를 구하면 된다.

모든 경우의 수를 확인해야 하므로 2차원 dp배열을 이용한다.
1<= i<= string1 의 길이, 1<= j <= string2 의 길이 일때 dp[i][j] 에 담기는 값의 의미는 string1에서 i까지 보고, string2에서 j까지 봤을 때 두 string의 공통 subsequence 중 가장 긴 것의 길이 를 의미한다!

위 그림처럼,
dp[1][1] : "A", "C"를 비교했을 때의 LCS 길이
dp[2][1] : "AC", "C"를 비교했을 때의 LCS 길이이다.
"C" 에서 LCS가 발견되었으므로 두 문자열에서 "C" 가 없었을 때, "A","" 를 비교했을 때의 LCS 길이 + 1이 dp[2][1] 에 들어가게 된다.

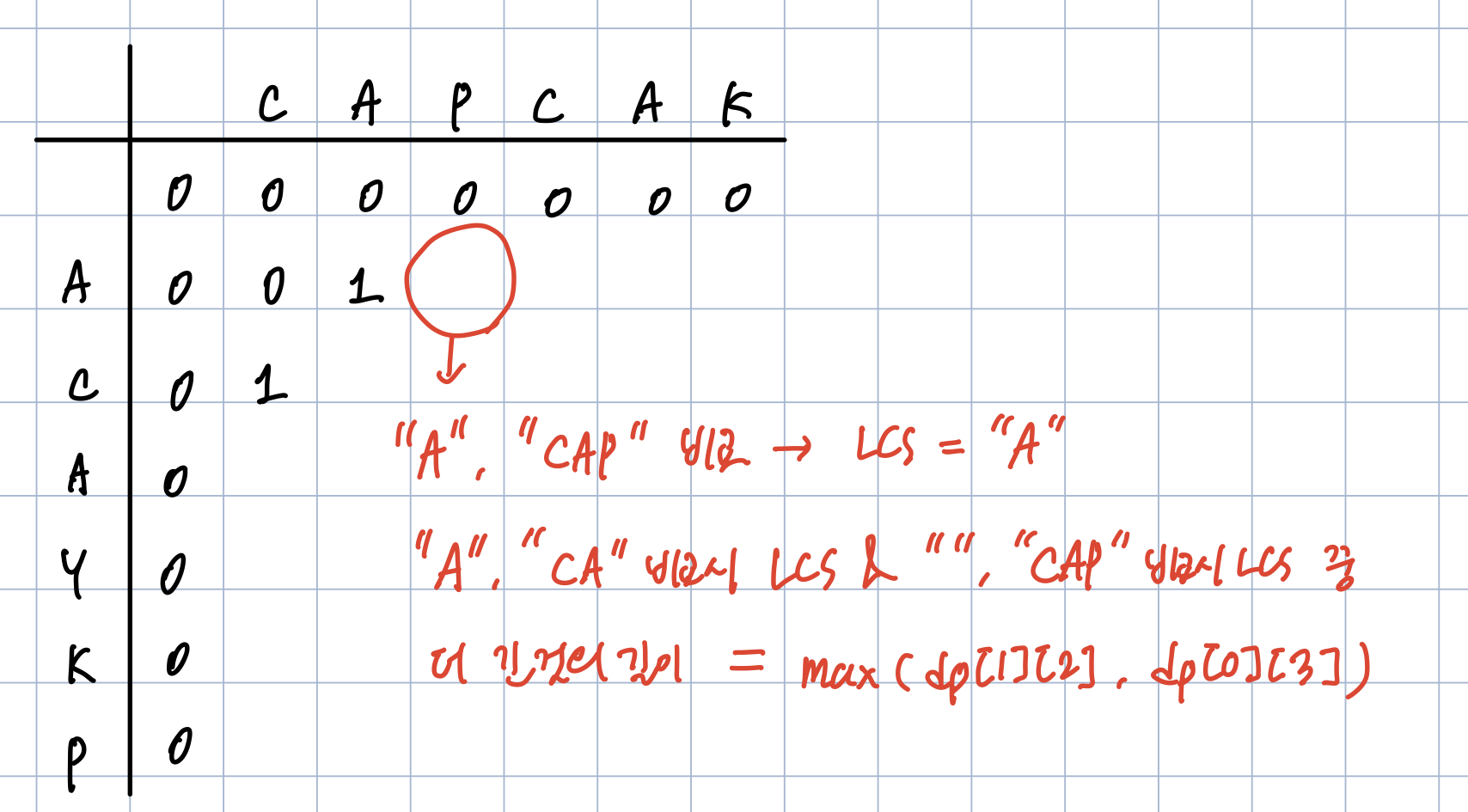
dp[1][3] : "A", "CAP" 비교시 LCS 길이
인데, 현재 A 와 P는 일치 하지 않고 이때까지의 LCS 는 "A" 이다.
이 때 dp[1][3] 에는 "A"-"CA" 비교시 LCS & ""-"CAP" 비교시의 LCS 중 더 긴 값이 들어가게 된다.

정리하면 점화식은,

dp[i][j]

• string1[i] == string2[j] 일 때 dp[i][j] = dp[i-1][j-1] + 1
• string1[i] != string2[j] 일 때 dp[i][j] = max(dp[i-1][j], dp[i][j-1])

로 정리 할 수 있다!

전체 코드

#include <iostream>
#include <vector>
#include <string>

// BOJ 9251 LCS
using namespace std;

int getLCS(string str1, string str2){
    int N = str1.length(), M = str2.size();
    vector<vector<int>> dp(N+1, vector<int>(M+1, 0));

    for (int i = 1; i <=N ; ++i) {
        for (int j = 1; j<=M; j++){
            if (str1[i-1] == str2[j-1]){
                dp[i][j] = dp[i-1][j-1] + 1;
            }else{
                dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
    }

    return dp[N][M];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    string str1, str2;
    cin>>str1>>str2;

    int longest = getLCS(str1, str2);
    cout<<longest;

    return 0;
}