오늘 풀어본 문제는 BOJ 2304 창고 다각형 문제이다!
역시나 작년 NHN 기출과 유사한 문제를 풀어보았고 예전에 풀어봤던 빗물 문제 와 매우 유사한 형태였다.
BOJ 2304 창고 다각형
N 개의 막대 기둥이 일렬로 세워져 있다. 기둥들의 폭은 모두 1 m이며 높이는 다를 수 있다. 이 기둥들을 이용하여 양철로 된 창고를 제작하려고 한다. 창고에는 모든 기둥이 들어간다. 이 창고의 지붕을 다음과 같이 만든다.
- 지붕은 수평 부분과 수직 부분으로 구성되며, 모두 연결되어야 한다.
- 지붕의 수평 부분은 반드시 어떤 기둥의 윗면과 닿아야 한다.
- 지붕의 수직 부분은 반드시 어떤 기둥의 옆면과 닿아야 한다.
- 지붕의 가장자리는 땅에 닿아야 한다.
- 비가 올 때 물이 고이지 않도록 지붕의 어떤 부분도 오목하게 들어간 부분이 없어야 한다.
그림 1은 창고를 옆에서 본 모습을 그린 것이다. 이 그림에서 굵은 선으로 표시된 부분이 지붕에 해당되고, 지붕과 땅으로 둘러싸인 다각형이 창고를 옆에서 본 모습이다. 이 다각형을 창고 다각형이라고 하자.
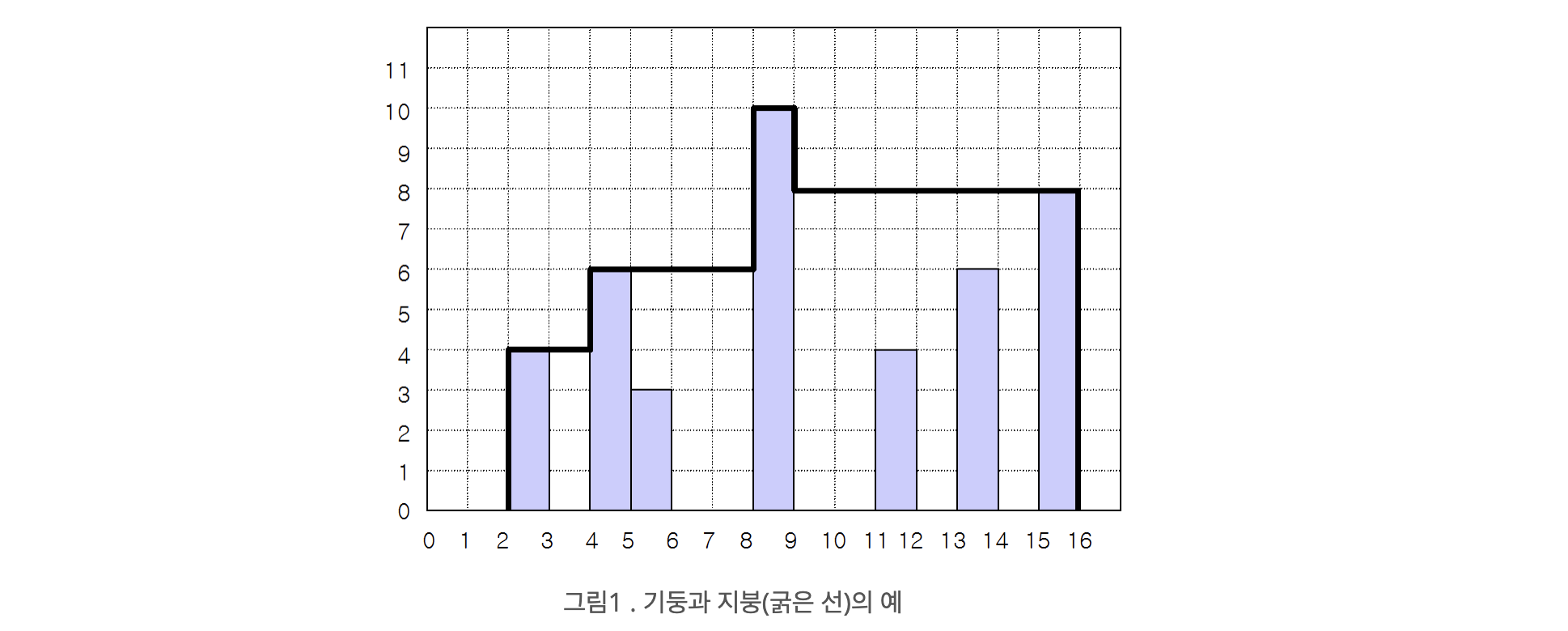
창고 주인은 창고 다각형의 면적이 가장 작은 창고를 만들기를 원한다. 그림 1에서 창고 다각형의 면적은 98 ㎡이고, 이 경우가 가장 작은 창고 다각형이다.
기둥들의 위치와 높이가 주어질 때, 가장 작은 창고 다각형의 면적을 구하는 프로그램을 작성하시오.
입출력
[입력]
첫 줄에는 기둥의 개수를 나타내는 정수 N이 주어진다. N은 1 이상 1,000 이하이다. 그 다음 N 개의 줄에는 각 줄에 각 기둥의 왼쪽 면의 위치를 나타내는 정수 L과 높이를 나타내는 정수 H가 한 개의 빈 칸을 사이에 두고 주어진다. L과 H는 둘 다 1 이상 1,000 이하이다.
[출력]
첫 줄에 창고 다각형의 면적을 나타내는 정수를 출력한다.
나의 풀이
입력 범위가 최대 1000 까지 였기 때문에 단순하고 빠르게 풀면 되는 문제였다.
입력되는 기둥을 그림처럼 2차원 배열에 입력하고 맨 아랫줄 부터 레이저를 쏘듯이 가장 처음 기둥이 나오는 지점 start와 가장 나중에 나오는 기둥 지점 end 를 구해 end-start+1 값을 더해가면 된다.
조금이나마 계산 횟수를 줄이기 위해 기둥중 가장 긴 높이와 가장 처음에 나오는 기둥의 위치, 가장 나중에 나오는 기둥의 위치를 입력받으면서 저장해 두고 그 범위 내에서만 탐색을 진행하였다.
내일 코테에서 나오면 좋겠다.. ^^
코드
#include <iostream>
#include <vector>
// boj 2304 창고 다각형, 구현, 실버 2
using namespace std;
vector<vector<int>> map(1001, vector<int>(1001, 0));
int getArea(int highest, int first, int last){
int area = 0;
for (int i = 0; i < highest; ++i) {
int start = -1, end = -1;
for (int j = first; j <= last; ++j) {
if (map[i][j]==1 ){
if (start == -1){
start = j;
end = j;
}else{
end = j;
}
}
}
area += end-start+1;
}
return area;
}
int main() {
ios::ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N;
cin>>N;
int highest = -1, first = 1001, last = -1;
for (int i = 0; i < N; ++i) {
int L, H;
cin>>L>>H;
if (highest < H) highest = H;
if (first > L) first = L;
if (last < L) last = L;
for (int j = 0; j < H; ++j) {
map[j][L] = 1;
}
}
cout<<getArea(highest, first, last);
return 0;
}