[알고리즘 풀이 분석] BOJ 14719 빗물

오늘의 두번째 문제는 BOJ 14719 빗물 이다! 구현 문제인데, 기출 문제 중 구현이 나온 경우가 꽤 많았고 1번 문제로 충분히 나올만 하다고 판단, 또 지난번에 구현 문제에 도전 했는데 생각보다 굉장히 오래걸렸던 끔찍한 기억이 떠올라 선택했다!

BOJ 14719 빗물

2차원 세계에 블록이 쌓여있다. 비가 오면 블록 사이에 빗물이 고인다.

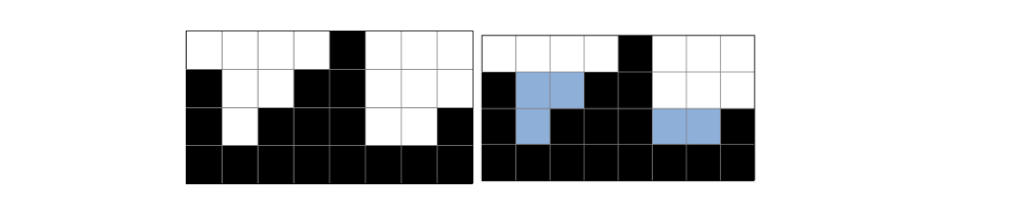
비는 충분히 많이 온다. 고이는 빗물의 총량은 얼마일까?

입출력

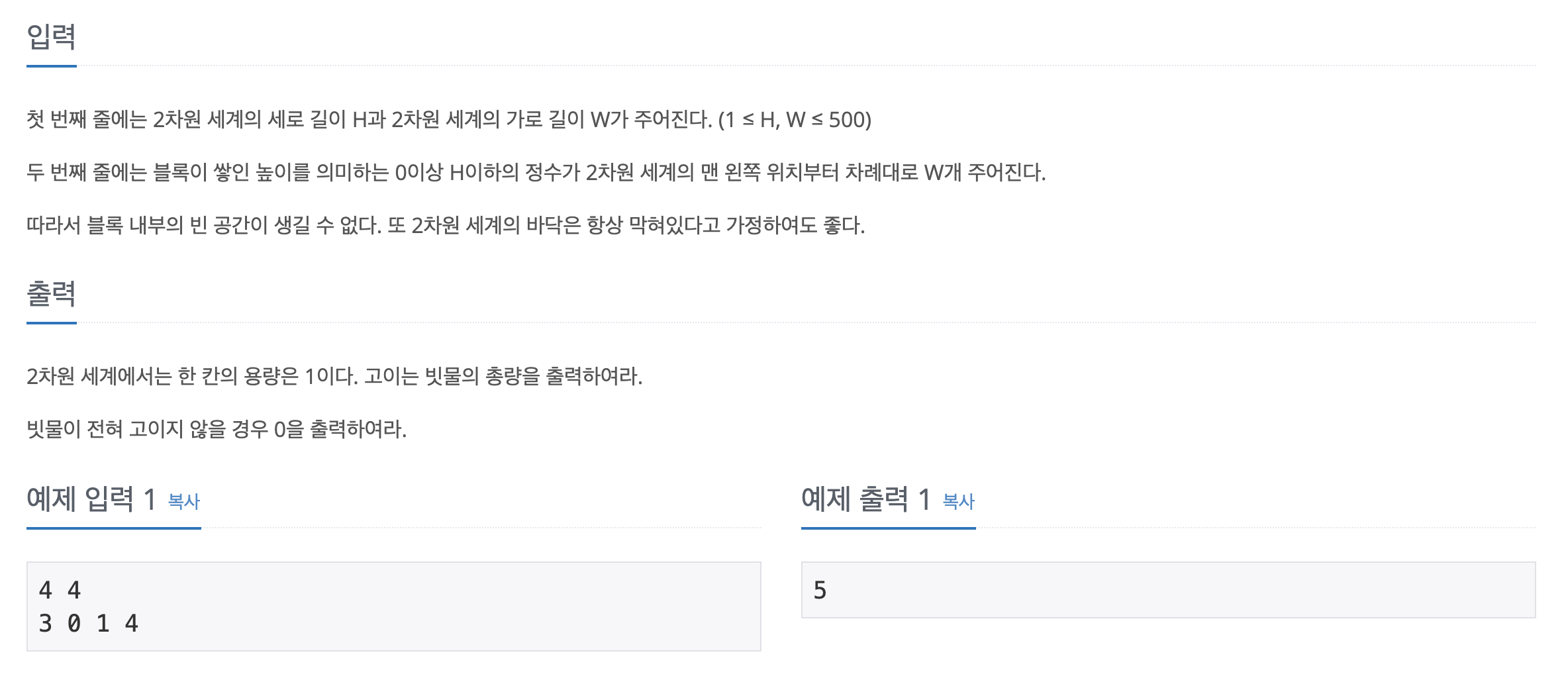
나의 풀이

주어진 블록 모양의 지도에 물이 고일 수 있는 칸의 수를 계산해 출력하는 문제이다.
처음엔 BFS 구나! (BFS 병걸린듯 ;;,,) 하면서 이르케 저렇게 해봤는데 할수록 뭔가 이상했다 ^^,,

일단 탐색은 아랫줄 부터 시작했다.
예시를 보니 좌우는 벽이 아니면 물이 고일 수 없지만 지도의 아래쪽은 벽이 아니어도 가장 아랫줄이면 물이 고일 수 있었기 때문이다. (H-1 행은 고일 수 있지만, 0 or W-1 열은 고일 수 없음)

BFS 가 적용될 수 있는지 없는지는 모르겠지만, 예를 들어

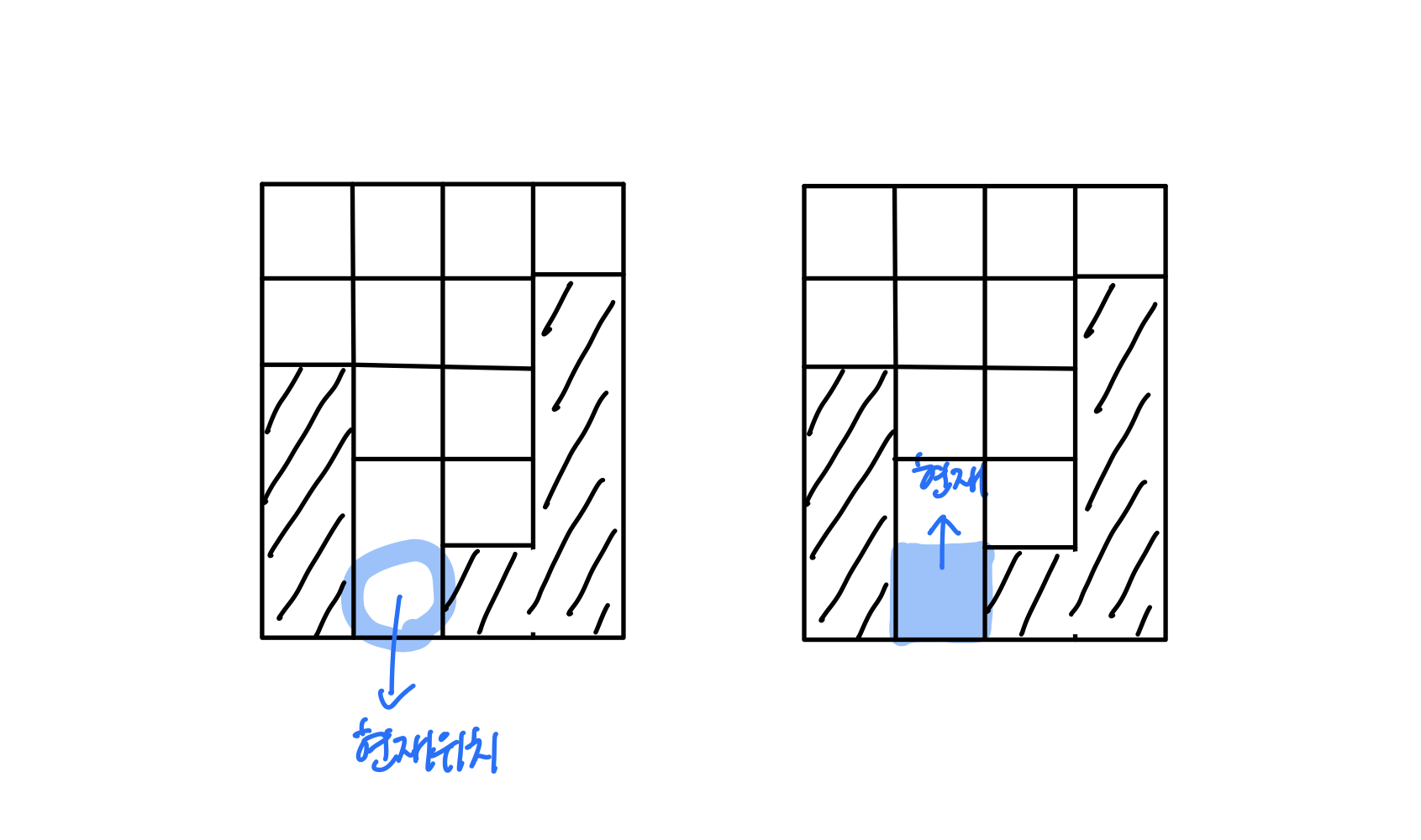
왼쪽과 같은 상황에서 (4,1) 이 고일 수 있는 칸임을 확인하고 그 윗칸인 (3,1) 로 이동했을 때 이 시점에선 인접한 (3,2)가 고일 수 있는 칸인지 확신할 수 없다.

때문에 확실하게 (3,1)를 BFS 과정에서 가져갈 수 없기 때문에 BFS가 적합하지 않다고 판단하였다.

또 구현 문제이고 골드V 문제인데 좀더 기본적인 알고리즘이 적용되지 않을까? 생각해보았다.

최종적으로 적용된 풀이는 매우 간단하다.
맨 아랫줄 부터, H-1 행부터 레이저를 쏜다고 생각하고 벽이 나오는지를 감지한다. 벽이 처음 나오면 이 벽은 시작벽이, 또 다시 벽이 나오는 순간 종료 벽이 완성된다. 이후 시작벽 - 종료벽 사이에 빈칸이 있는지 확인하고 있다면 해당 칸 수대로 빗물칸으로 더해준다.

빗물이 더해진 이후엔 다시 종료벽 부터 탐색을 시작해서 위와 같은 탐색을 반복한다. 지도상에서 좌우 방향은 해당 칸이 지도 끝에 위치한다고 해도 고일 수 없다는걸 문제의 예시 3을 통해 알 수 있으므로 반드시 시작벽과 종료벽이 모두 존재해야 한다는 조건을 걸어준다.

코드

#include <iostream>
#include <vector>

// BOJ 14719 빗물
using namespace std;

int getRain(vector<vector<int>> map){
    int rain = 0;
    int H = map.size();
    int W = map[0].size();

    for (int i = H-1; i >=0 ; i--) {
        // 벽 시작, 종료 여부와 해당 지점 index
        bool start = false, end = false;
        int left = -1, right = -1;

        for (int j = 0; j < W; ++j) {
            if (map[i][j] == 1){  // 벽을 만나면
                if (!start){  // 시작되는 벽이면
                    start = true;
                    left = j;
                } else{  // 끝나는 벽 찾으면
                    end = true;
                    right = j;

                    if (start && end && right-left > 1){  // 두 벽 사이 공간이 있으면
                        rain += right-left-1;
                    }

                    j--; // 다시 종료한 벽부터 탐색해야 
                    start = false;
                    end = false;
                }
            }
        }
    }

    return rain;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int H, W;
    cin>>H>>W;

    vector<vector<int>> map(H, vector<int>(W, 0));

    int wall;
    for (int i = 0; i < W; ++i) {
        cin>>wall;
        for (int j = 0; j < wall; ++j) {
            map[H-1-j][i] = 1;
        }
    }

    int rain = getRain(map);
    cout<<rain;

    return 0;
}