[알고리즘 풀이 분석] Programmers N으로 표현

태생적으로 DP를 싫어하는 병이 있는지라,,
미루고 미루던 DP 를 오늘 드디어 시작했다

뭐 처음 풀어보는건 당연 아니지만, 프로그래머스 알고리즘 중에 DP 만이 유일하겤ㅋㅋㅋㅋ 0/6 으로 남아있는 꼴이 맘에 들지 않아서 오늘 2문제를 해치웠고, 그 중 하나를 포스팅 해 보고자 한다

프로그래머스 N으로 표현

문제 링크

12 = (55 + 5) / 5 와 같이 N, number 가 주어지면 N만을 이용해 number 를 표현하고 그 중 가장 적은 수의 N이 사용되는 경우를 찾으면 되는 문제이다

제한 사항과 입출력

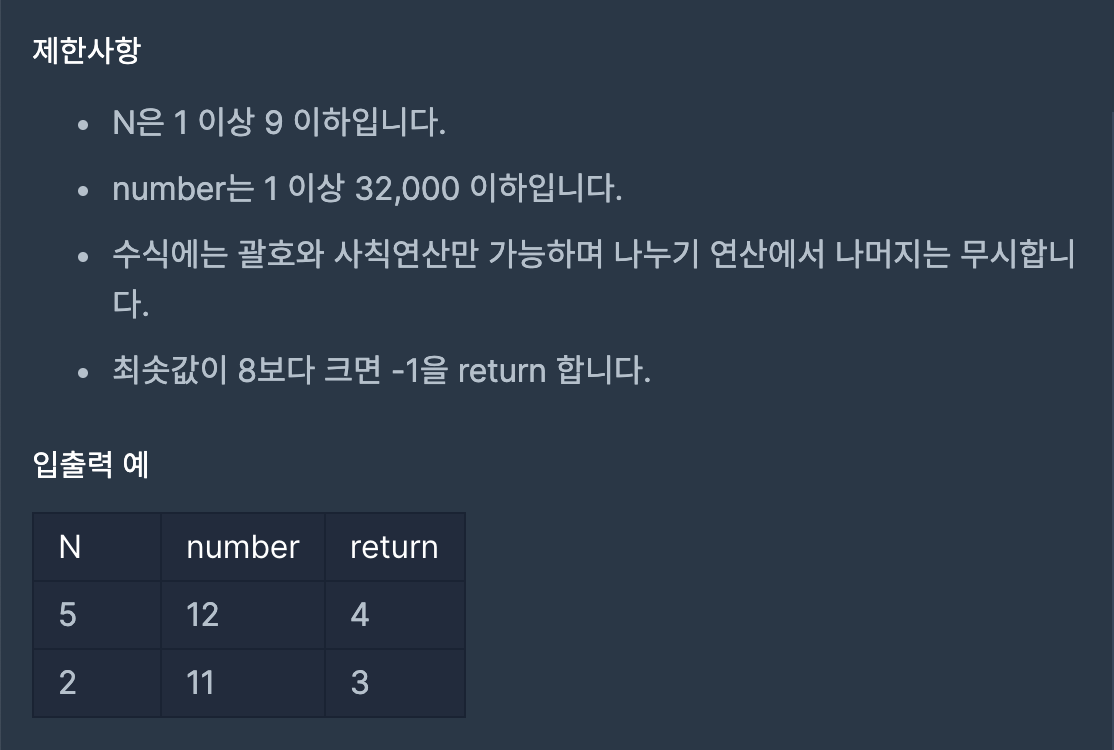
나의 풀이

처음에 나는 1 부터 주어진 number 까지 bottom-up 방식으로 해결하고자 생각했다. i 를 표현하기 위해선 이 전에 구해 놓은 memorization[1 ~ i-1] 내용을 이용해 최솟 값을 구하고, 이렇게 구한 memorization[i] 가 다시 i+1 을 구하는데 이용되는 방식으로 해결을 시도하였다!

결과는 땡이다 땡!

나의 얄팍한 DP 지식에 의존한지라 이런식의 bottom-up 방식이 답이라고 지정해 놓은 탓인지, 규칙성을 발견하려 이리 저리 적어 보아도 특별한 규칙을 알 수 없었고 왜 안되지,, 하면서도 다른 방식을 시도 해 보지 않았다 ㅠㅠ

결국 한 블로그 글을 참고해 새로운 방식으로 접근하여 해결 할 수 있었다

해결 풀이

통과된 풀이의 핵심 개념은 생각보다 단순하다
주어진 정수 N을 i 개 사용할 수 있는 수들을 모아 집합(i)라 하고, 집합(n)을 만들 때에는,

• 집합(n-1) & 집합(1)
• 집합(n-2) & 집합(2)
• 집합(n-3) & 집합(3)
  ...
• 집합(1) & 집합(n-1)

을 이용해 N을 n개 이용해 만들 수 있는 수 들의 모임, 집합(n)을 완성하는 방식이다.

여기서 추가로 챙겨줘야 하는 녀석이 있는데, N을 n개 나열한 NNN 과 같은 형태의 정수이다

설명이 매우 추상적으로 보이니 구체적인 예시로 설명해보자!

N = 2, number = 11 인 경우!

• 2를 1개 사용해서 만들 수 있는 정수 : 2
• 2를 2개 사용해서 만들 수 있는 정수 : 2+2, (2-2), 2*2, 2/2, 22
  이 때, 2-2 = 0 이고, 우리가 찾고자 하는 number을 1이상 32,000 이하의 정수이니 제외 시킬 수 있다!
  즉, 2를 2개 사용하여 만들 수 있는 정수는 22, 4, 1 세가지 이다
• 2를 3개 사용해서 만들 수 있는 수
  • 덧셈) 2+22 2+4, 2+1, (22+2, 22+4, 22+1)
  • 뺄셈) 2-22, 2-4, 2-1, 22-2, 4-2, 1-2
  • 곱셈) 222, 24, 21, (222, 42, 12)
  • 나눗셈) 2/22, 2/4, 2/1, 22/2, 4/2, 2/1
  • 그리고, 222!

그런데 곱셈과 덧셈은 교환 법칙이 성립하기 때문에 같은 연산 결과가 두번씩 들어가 있는 것을 알 수 있기에! 괄호 쳐진 수들은 계산 될 필요가 없다!

또한 뺄셈의 경우 연산 결과가 1보다 작으면 제외 시켜 나눗셈 연산 시 0으로 나누는 오류가 발생하는 것 까지 함께 예방할 수 있다!

이러한 식으로 1~ 8 방향으로 2차원 벡터를 완성해가며, 연산 한 결과 number 일 경우 탐색을 중단하고 정답을 반환하는 방식으로 코드를 작성하여 통과하였다!

코드

#include <vector>
#include <algorithm>

using namespace std;

// N을 times 번 이어붙이 수 반환
int getConnectedNumber(int N, int times){
    int ans = 0;

    for (int i = 0; i < times-1; ++i) {
        ans *= 10;
        ans += (N * 10);
    }
    ans += N;

    return ans;
}

// 사칙 연산을 통해 만들 수 있는 수 추가, number 인지 확인하면 반환
bool basicOperating(vector<vector<int>> & sets, int a, int b, int number){
    int n = a+b;

    for (int i = 0; i < sets[a].size(); ++i) {
        for (int j = 0; j < sets[b].size(); ++j) {
            int subtract, divide, sum, multiple;
            subtract = sets[a][i] - sets[b][j];
            divide = sets[a][i] / sets[b][j];

            // 뺀 값과 나눈 값은 1 이상일 때에만 적용
            if (subtract >= 1) sets[n].push_back(subtract);
            if (divide >= 1) sets[n].push_back(divide);

            if (a >= b) {
                sum = sets[a][i] + sets[b][j];
                multiple = sets[a][i] * sets[b][j];

                sets[n].push_back(sum);
                sets[n].push_back(multiple);
            }

            // 찾던 수라면 탐색 중단하고 반환
            if (subtract == number || divide == number || sum == number || multiple == number) return true;

        }
    }

    return false;
}

int solution(int N, int number) {
    int answer = 0;
    bool found = false;
    vector<vector<int>> numsUsingN(9);
    
    vector<int> base = {N, N*10 + N, N+N, N*N, N/N};

    if (base[0] == number) return 1;
    numsUsingN[1].push_back(N);
    
    for (int i = 1; i < base.size() ; ++i) {
        if (base[i] == number) return 2;
        numsUsingN[2].push_back(base[i]);
    }
    
    numsUsingN[2].erase(unique(numsUsingN[2].begin(), numsUsingN[2].end()), numsUsingN[2].end());

    for (int i = 3; i <= 8 ; ++i) {
        int connected = getConnectedNumber(N, i);

        if (connected == number) {
            found = true;
            break;
        }else{
            numsUsingN[i].push_back(connected);
        }

        for (int j = i-1; j >= 1 ; j--) {
            if (basicOperating(numsUsingN, j, i-j, number)){
                answer = i;
                found = true;
                break;
            }
        }

        if (found) break;
    }

    if (!found) answer = -1;

    return answer;
}

참고 자료