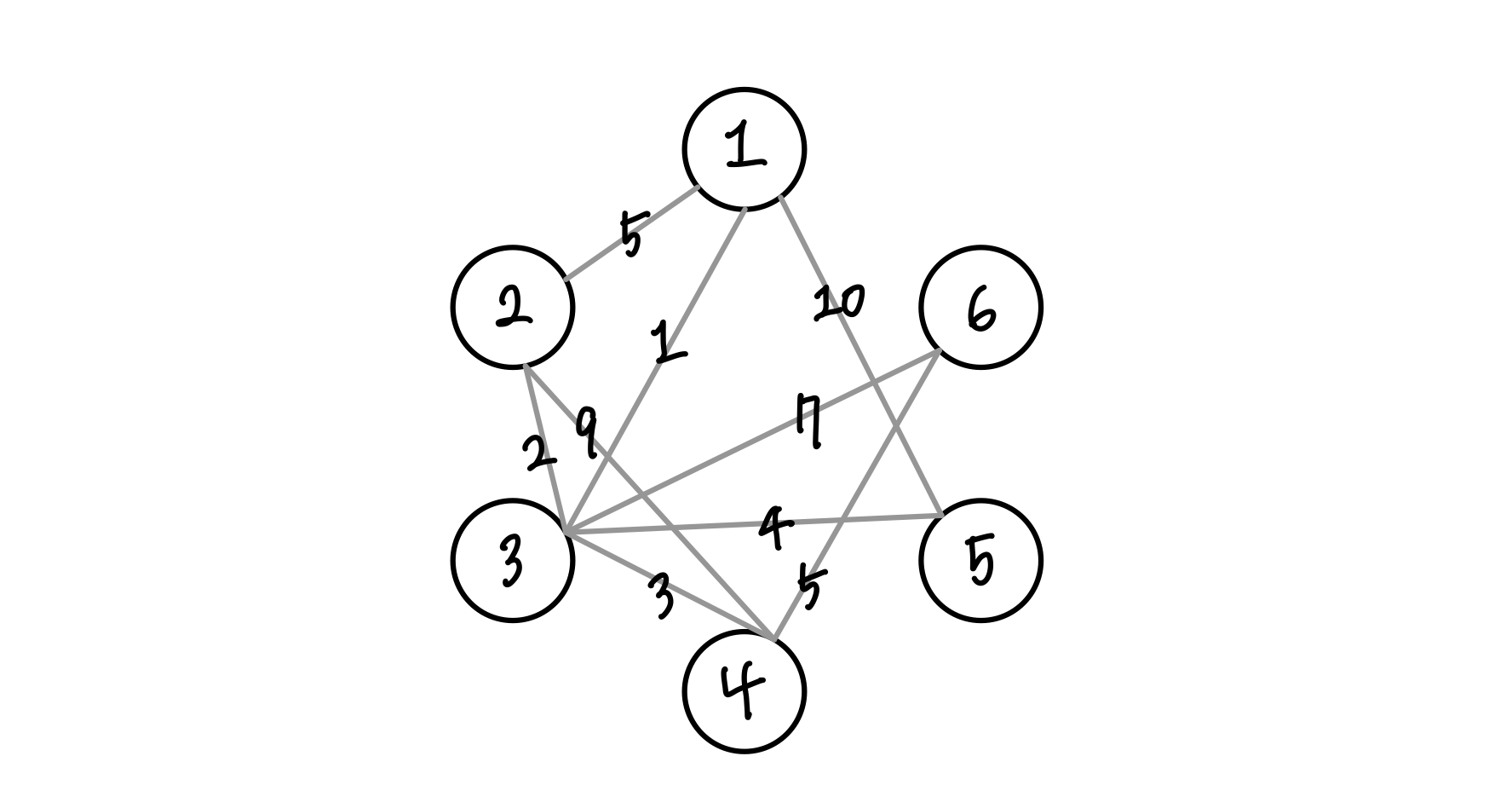
어제 풀었던 문제를 통해 Dijkstra, Floyd-Warshall 알고리즘에 대한 이해가 탄탄하지 못하다고 느껴서 복습겹 공부하고 코드로 구현해 본다!
Dijkstra 다익스트라
개념
다익스트라 알고리즘의 용도는 "한 정점으로 부터 다른 지점까지의 최소 거리를 알고자 할 때" 이다!
어제도 결론적으로는 모든 정점에서 다른 정점까지의 최소 거리가 필요했는데 알고리즘의 용도를 제대로 파악하지 못하고 있어서 엉뚱하게 다익스트라로 몇시간을 쏟았다.
총 6개의 정점이 있는 그래프에서 노드 1번부터 2,3,4,5,6번 노드로 가는 최소 비용을 구한다고 가정해보자.
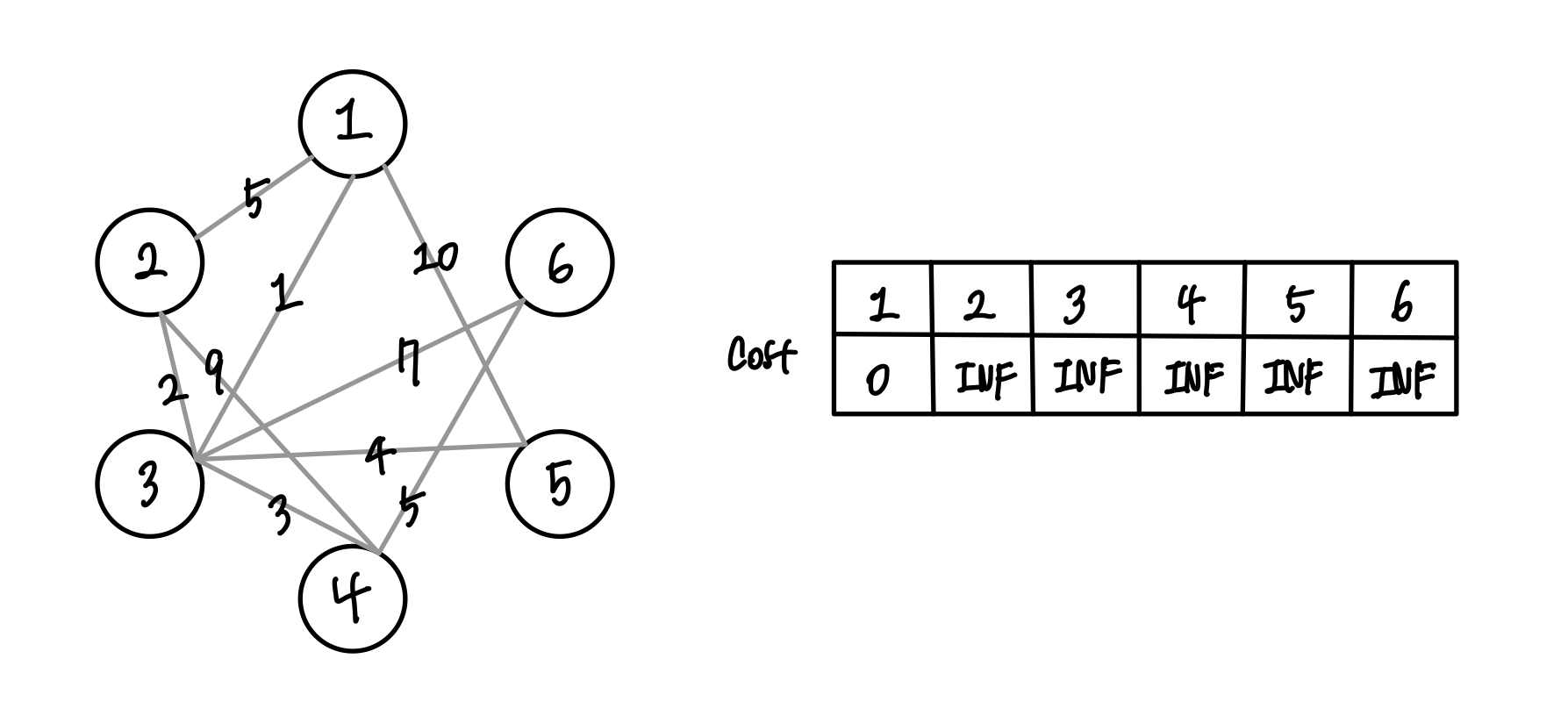
초기 상태는 1에서 다른 지점까지 가는 비용을 계산하기 전 출발 지점 1을 제외한 cost는 모두 갈 수 없음을 뜻하는 매우 큰 값 INF 로 되어 있다.
이 때 현재 가장 cost 값이 적은 출발지점인 1을 중간 지점으로 선택하고 1->1->(2-6) 으로 가는 비용을 갱신해준다. 1->1->2 의 경우 cost[1] + 간선(1->2)의 값 0+5 = 5 이고 이는 현재의 cost[2] 값 INF 보다 작으므로 갱신되어 cost[2] = 5로 변경된다.
1에 연결되어 있는 간선 값들을 적용하는 것이지만 알고리즘의 통일성을 위해 이와 같이 생각하는게 오히려 간단할 것 같다.
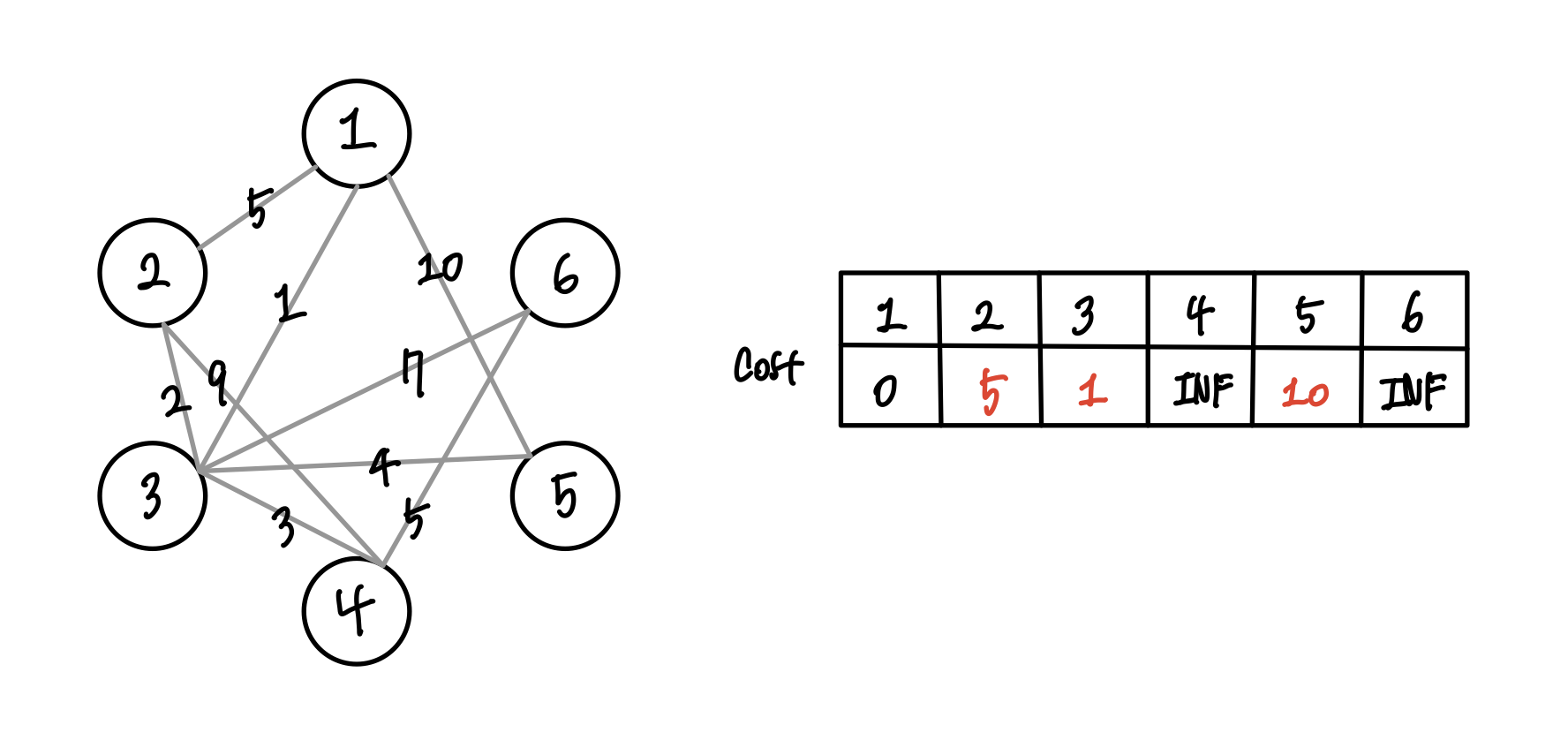
이와 같은 과정을 통해 노드 3,5 역시 cost 값이 갱신되고, 1로부터의 간선이 존재 하지 않는 노드 4,6 은 여전히 cost 값이 INF 로 유지된다.
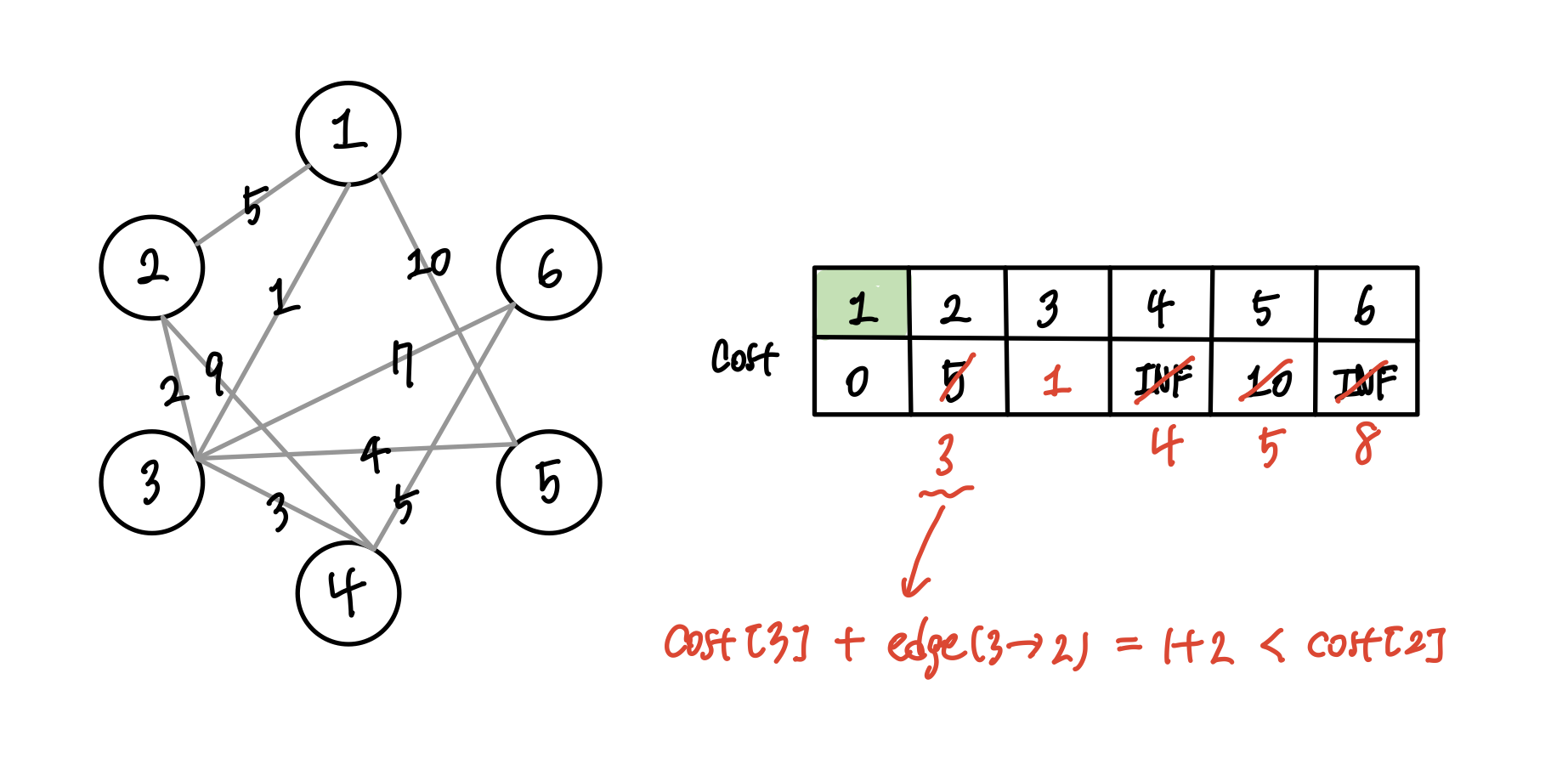
이제 갱신된 노드들 중에서 가장 최소 비용을 갖는 노드, 3을 거쳐 다른 노드로 가보자. cost[3] = 1 이고 3에 연결된 간선 값에 따라 저장되어 있는 cost 값 보다 작으면 갱신된다.

다시 갱신된 노드들 중에서 가장 작은 값을 갖는 노드, 2를 선택해 거쳐가는 노드로 지정하고 위와 같은 과정을 반복한다. 이때 이미 중간 지점으로 선택되었던 1,3을 제외한 2,4,5,6 중에서 2를 고르게 된다.
이처럼 갱신된 비용 중 가장 저렴한 비용인 노드를 고르는 과정에서 선형 탐색을 이용하면 시간 복잡도는 O(N^N) 이고 노드는 많은데 간선이 매우 적은 극단적인 경우에 굉장히 시간이 굉장히 낭비되는 불상사가 생길 수 있다.
때문에 이럴 때 선형 탐색보단 우선순위 큐를 사용하여 가장 비용이 적은 노드를 빠르게 찾아내어 시간 복잡도 O(N * logN) 을 만족시키며 효율성을 개선시킬 수 있다.
코드
void linearDijkstra(){
vector<int> visited(6, false);
vector<int> cost(6, INF);
for (int i = 0; i < 6; ++i) {
cost[i] = edge[start][i];
}
visited[0] = true;
for (int i = 0; i < 6-2; ++i) {
int minCost = INF;
int middleNode;
for (int j = 0; j < 6; ++j) {
if ( !visited[j] && minCost > cost[j]){
minCost = cost[j];
middleNode = j;
}
}
visited[middleNode] = true;
for (int j = 0; j < 6; ++j) {
if (j!=start && cost[middleNode] + edge[middleNode][j] < cost[j]){
cost[j] = cost[middleNode] + edge[middleNode][j];
}
}
}
cout<<"------------ Linear Dijkstra -------------"<<'\n';
for (int i = 0; i < 6; ++i) {
cout<<cost[i]<<' ';
}
cout<<'\n';
}
void heapDijkstra() {
vector<int> cost(6, INF);
cost[start] = 0;
priority_queue<pair<int, int>> pq; // <노드 번호, -비용> 저장
pq.push(make_pair(start, 0));
while (!pq.empty()){
int middleNode = pq.top().first;
int middleCost = -pq.top().second;
pq.pop();
if(middleCost > cost[middleNode]) continue;
for (int i = 0; i < 6; ++i) {
if (i!=start && edge[middleNode][i] != INF && middleCost+edge[middleNode][i] < cost[i]){
cost[i] = middleCost + edge[middleNode][i];
pq.push(make_pair(i, -(middleCost + edge[middleNode][i])));
}
}
}
cout<<"------------ Heap Dijkstra -------------"<<'\n';
for (int i = 0; i < 6; ++i) {
cout<<cost[i]<<' ';
}
cout<<'\n';
}Floyd-Warshall 플로이드 와샬
개념
플로이드 와샬의 용도는 "모든 정점으로 부터 다른 정점들로 가는 최소 비용을 알고자 할 때" 이다.
뭐 말하자면 다익스트라의 확장판..? 인가
하지만 과정은 훨씬 간단하다.
다익스트라 알고리즘을 모든 정점에 대해 적용하는 것과 같은 방식이기 때문에 당연히 n * n 크기의 2차원 배열이 필요하다.
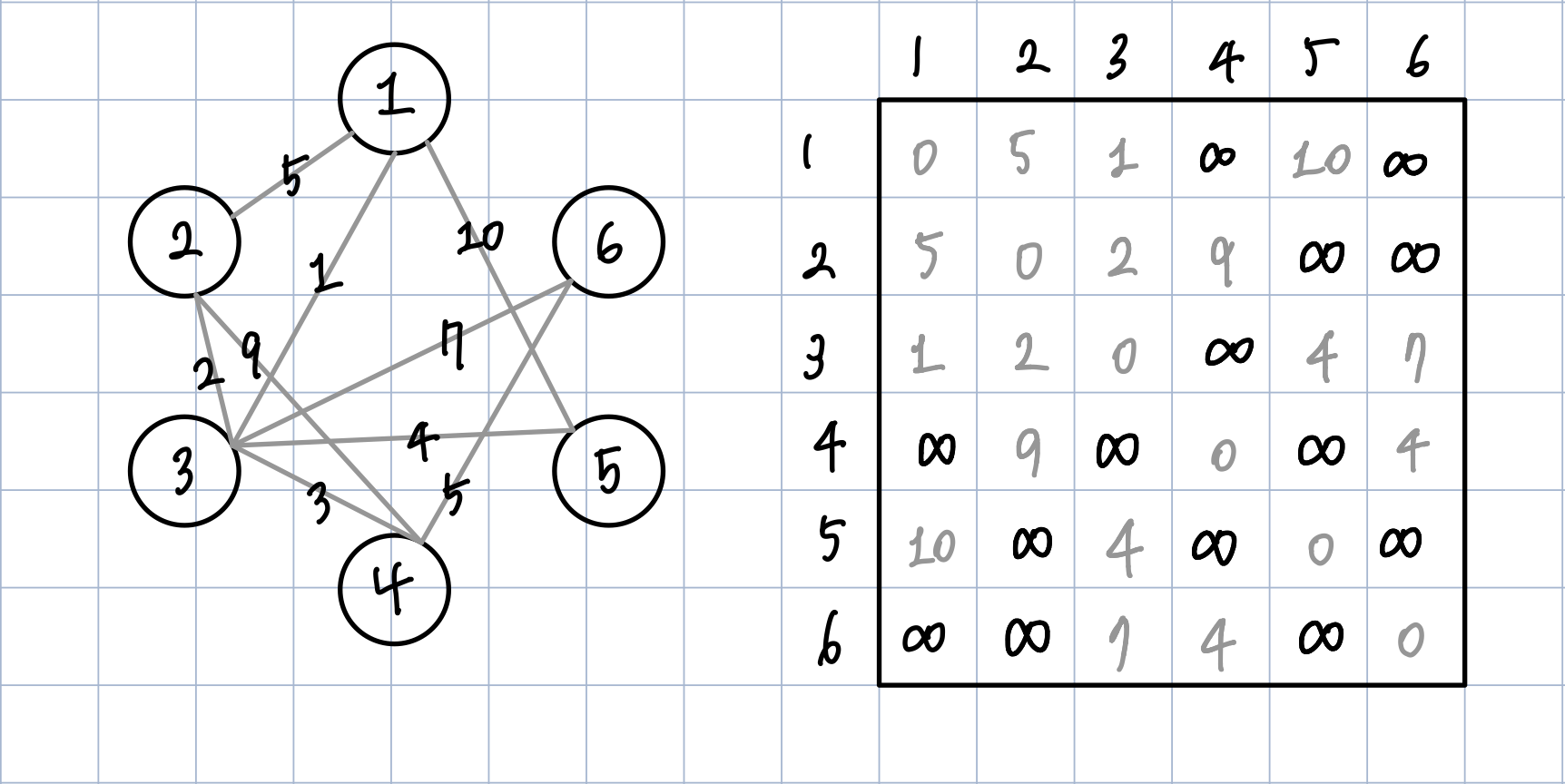
같은 그래프를 대상으로 초기 상태, 즉 갱신되기 전 비용은 위 그림과 같을 것이다. 간선이 연결되어 있지 않는 이웃 노드의 경우 해당 비용은 이동할 수 없음을 나타내는 무한대 값 (INF, 매우 큰 값) 으로 나타내어진다.
플로이드 와샬 에서는 모든 정점을 출발점으로 잡아야 하기 때문에 가장 적은 비용을 가지는 중간 지점을 굳이 고를 이유가 없다. 어차피 N * N 개의 칸을 모두 확인하기 때문이다.
이제 순차적으로 1-6까지의 노드를 중간 지점으로 잡아 cost[i][j]를 최솟값으로 갱신한다. 중간 지점이 k라 할 때 cost[i][j] > cost[i][k] + edge[k-j] 라면 cost[i][j] 값은 갱신된다.
모든 중간 지점 k 노드에 대해 cost 배열 갱신이 완료되면 완성된 cost[i][j] 엔 노드 i->j로 이동하는 가장 적은 비용이 적히게 된다.
코드
void floydWarshall() {
for (int middle = 0; middle < 6; ++middle) {
for (int i = 0; i < 6; ++i) {
for (int j = 0; j < 6; ++j) {
if (edge[i][j] > edge[i][middle] + edge[middle][j]){
edge[i][j] = edge[i][middle] + edge[middle][j];
}
}
}
}
cout<<"------------ Floyd Warshall -------------"<<'\n';
for (int i = 0; i < 6; ++i) {
for (int j = 0; j < 6; ++j) {
if (edge[i][j]<INF) cout<<edge[i][j]<<' ';
else cout<<"INF"<<' ';
}
cout<<'\n';
}
cout<<'\n';
}전체 실행 코드
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int start = 0;
int INF = 100000;
vector<vector<int>> edge;
void linearDijkstra(){
vector<int> visited(6, false);
vector<int> cost(6, INF);
for (int i = 0; i < 6; ++i) {
cost[i] = edge[start][i];
}
visited[0] = true;
for (int i = 0; i < 6-2; ++i) {
int minCost = INF;
int middleNode;
for (int j = 0; j < 6; ++j) {
if ( !visited[j] && minCost > cost[j]){
minCost = cost[j];
middleNode = j;
}
}
visited[middleNode] = true;
for (int j = 0; j < 6; ++j) {
if (j!=start && cost[middleNode] + edge[middleNode][j] < cost[j]){
cost[j] = cost[middleNode] + edge[middleNode][j];
}
}
}
cout<<"------------ Linear Dijkstra -------------"<<'\n';
for (int i = 0; i < 6; ++i) {
cout<<cost[i]<<' ';
}
cout<<'\n';
}
void heapDijkstra() {
vector<int> cost(6, INF);
cost[start] = 0;
priority_queue<pair<int, int>> pq; // <노드 번호, -비용> 저장
pq.push(make_pair(start, 0));
while (!pq.empty()){
int middleNode = pq.top().first;
int middleCost = -pq.top().second;
pq.pop();
if(middleCost > cost[middleNode]) continue;
for (int i = 0; i < 6; ++i) {
if (i!=start && edge[middleNode][i] != INF && middleCost+edge[middleNode][i] < cost[i]){
cost[i] = middleCost + edge[middleNode][i];
pq.push(make_pair(i, -(middleCost + edge[middleNode][i])));
}
}
}
cout<<"------------ Heap Dijkstra -------------"<<'\n';
for (int i = 0; i < 6; ++i) {
cout<<cost[i]<<' ';
}
cout<<'\n';
}
void floydWarshall() {
for (int middle = 0; middle < 6; ++middle) {
for (int i = 0; i < 6; ++i) {
for (int j = 0; j < 6; ++j) {
if (edge[i][j] > edge[i][middle] + edge[middle][j]){
edge[i][j] = edge[i][middle] + edge[middle][j];
}
}
}
}
cout<<"------------ Floyd Warshall -------------"<<'\n';
for (int i = 0; i < 6; ++i) {
for (int j = 0; j < 6; ++j) {
if (edge[i][j]<INF) cout<<edge[i][j]<<' ';
else cout<<"INF"<<' ';
}
cout<<'\n';
}
cout<<'\n';
}
int main() {
edge = { {0,5,1,INF,10,INF},
{5,0,2,9,INF,INF},
{1,2,0,3,4,7},
{INF,9,3,0,INF,5},
{10,INF,4,INF,0,INF},
{INF,INF,7,5,INF,0}};
linearDijkstra();
heapDijkstra();
floydWarshall();
return 0;
}