아래와 같이 한 방향으로 나열된 트리를 균형 잡히지 않은 트리라고 합니다.
일반적인 트리는 시간복잡도가 이지만 균형잡히지 않은 트리는 시간 복잡도가 연결리트스와 같은 이기 때문에 효율적이지 않습니다.

이런 불균형한 트리를 이진 탐색 트리로 만들기위해 노드의 위치를 바꾸는 과정을 회전이라고 합니다.
일반적인 트리는 루트가 항상 중간 숫자를 가집니다.
하지만 균형 잡히지 않은 트리는 이 균형이 깨져있기 때문에 이 균형을 잡아야합니다.
불균형이 왼쪽 서브트리에서 나타나는 경우
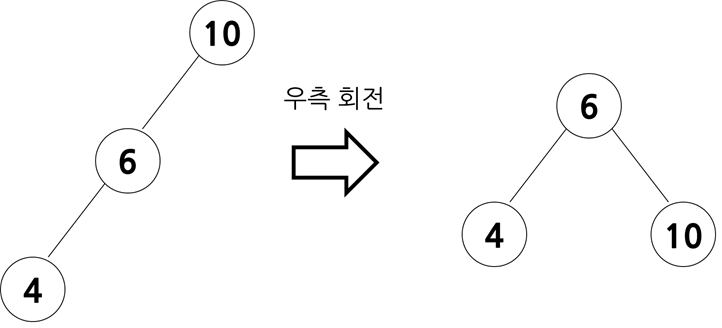
위 트리의 크기 관계는 10(조부모 노드) > 6(부모 노드) > 4(자식 노드)입니다.
우측 회전을 하여 조부모 노드를 부모 노드의 오른쪽 자식 노드 위치로 옮겨줍니다.
불균형이 오른쪽 서브트리에서 나타날 경우
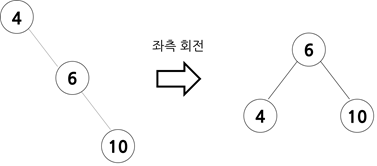
크기 관계는 10(조부모 노드) < 6(부모 노드) < 4(자식 노드)입니다.
좌측 회전을 하여 조부모 노드를 부모 노드의 왼쪽 자식 노드 위치로 옮겨줍니다.
하지만 트리가 한쪽으로 치우친 경우가 아닌 경우 우측 회전과 좌측 회전을 모두 사용하여 불균형을 해소합니다.
불균형이 오른쪽 자식의 왼쪽 서브 트리에서 나타날 경우
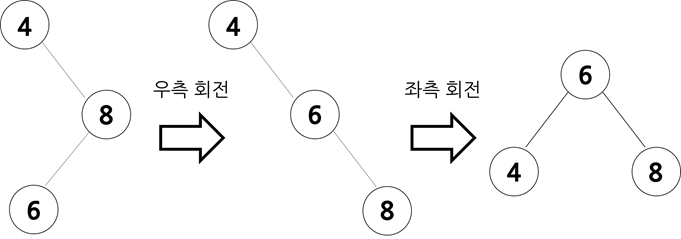
크기 관계는 8(부모 노드) > 6(자식 노드) > 4(조부모 노드)입니다.
자식 노드에 대해 부모 노드를 우측 회전 후 좌측 회전을 하여 조부모 노드를 부모 노드의 왼쪽 자식 노드 위치로 옮겨줍니다.
불균형이 왼쪽 자식의 오른쪽 서브 트리에서 나타날 경우
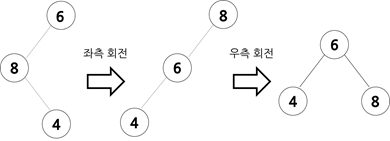
크기 관계는 8(부모 노드) > 6(조부모 노드) > 4(자식 노드)입니다.
자식 노드에 대해 부모 노드를 좌측 회전 후 우측 회전을 하여 조부모 노드를 부모 노드의 오른쪽 자식 노드 위치로 옮겨줍니다.
이렇게 트리를 회전을 하면 항상 중간 크기의 요소가 루트로 올 수 있습니다.
위 회전으로 코드로 나타내보겠습니다.
트리를 회전하기 위해서는 임시 포인터를 사용해야합니다.
좌측회전
회전은 항상 조부모 노드에서 시작하기 때문에 임시 포인터를 조부모 노드의 오른쪽 자식을 가리키게 하겠습니다.
그리고 오른쪽 자식을 임시포인터의 왼쪽 자식이 되게하겠습니다.
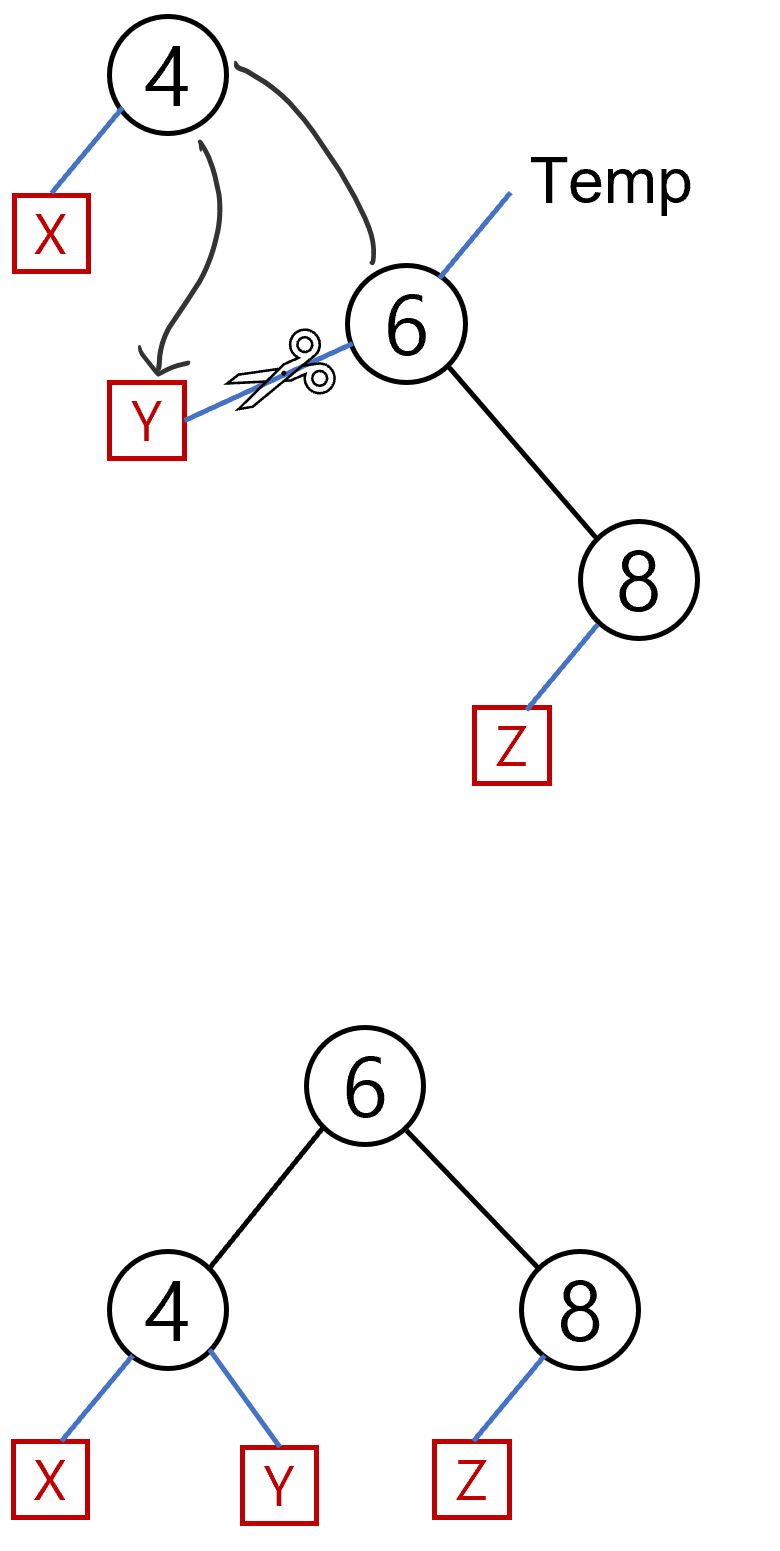
이때 x,y,z 는 null을 가리킬수도 있고 다른 노드가 있을 수 있습니다.
하지만 회전은 동일한 방식으로 작동합니다.
그리고 조부모의 오른쪽 자식을 임시 포인터의 왼쪽 자식으로 설정하겠습니다.
그러면 y와의 연결이 끊어지게됩니다.
그리고 임시 변수의 왼쪽자식을 조부모 노드와 같아만듭니다.
마지막으로 temp를 조부모 노드로 사용하면 됩니다.
// 좌측 회전: 조부모 노드를 부모 노드의 왼쪽 자식 노드 위치로 옮깁니다.
public Node<E> leftRotate(Node<E> node){
Node<E> tmp = node.right; // node의 오른쪽 자식을 임시포인터로 생성
node.right = tmp.left; // node의 오른쪽 자식을 임시포인터의 왼쪽 자식으로 설정
tmp.left = node; // 임시포인터의 왼쪽 자식을 회전시켜야하는 노드로 설정
return tmp; // 임시포인터 반환
}우측회전
우측회전도 비슷합니다.
조부모의 왼쪽 자식을 임시포인터로 설정하고 임시포인터를 조부모의 왼쪽 자식으로 설정합니다.
그러면 동일하게 조부모의 왼쪽 자식을 임시 포인터의 오른쪽 자식으로 설정하고 임시포인터의 오른쪽 자식으로 조부모 노드로 설정할 수 있습니다.
// 우측 회전: 조부모 노드를 부모 노드의 오른쪽 자식 노드 위치로 옮깁니다.
public Node<E> leftRotate(Node<E> node){
Node<E> tmp = node.left;
node.left = tmp.right;
tmp.right = node;
return tmp;
}
트리가 한쪽으로 치우치지 않았을 경우 우측회전과 좌측회전을 둘 다 사용해야합니다.
우측-좌측회전
// 우측 회전 후 좌측 회전
public Node<E> rightLeftRotate(Node<E> node){
node.right = rightRotate(node.right);
return leftRotate(node);
}
좌측-우측회전
// 좌측 회전 후 우측 회전
public Node<E> leftRightRotate(Node<E> node){
node.left = leftRotate(node.left);
return rightRotate(node);
}