트리 - 노드 클래스, add, contains

노드 클래스

위의 그림처럼 트리는 항상 작은 값이 왼쪽에 와야합니다.

그렇기 때문에 어떤 값을 찾고싶다면 루트의 값보다 큰지 작은지 확인을 해야합니다.

이렇게 위에서부터 비교를 하며 내려가면 남은 데이터의 반은 항상 무시하고, 간 복잡도는 $log n$를 가집니다.

연결리스트가 next 포인터를 가지는 것처럼 트리는 parent, left, right포인터를 가지겠습니다.

그렇기 때문에 최대 세가지의 포인터가 같은 노드를 가르키게 됩니다.

우선은 left와 right포인터만을 가지고 아래와 같이 구현해보겠습니다.

class Node<E> {
	E data;
	Node <E> left, right;
    
	public Node(E obj){
		this.data = obj;
		left=right=null;
	}
}

data 와 left, right 변수를 지정하고 생성자를 만들었습니다.

생성자는 트리에 저장할 객체를 받아와서 data에 저장하고 left와 right는 null로 지정했습니다.

---

add

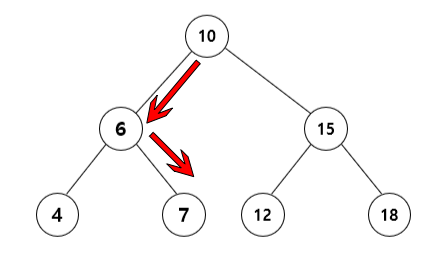
트리에 무엇인가를 추가할 때는 먼저 루트에서부터 값의 대소를 비교하면서 null인 부분까지 찾아 내려가야합니다.

하지만 찾아 내려가기까지 몇개의 노드를 살펴봐야하는지 알 수 없습니다 .

그렇기 때문에 대부분의 트리 메소드는 재귀함수로 이루어져 있습니다.

이 재귀함수는 루트가 왼쪽 혹은 오른쪽 노드로 값을 넘겨주고, 값을 넘겨 받은 노드는 또 다시 왼쪽 혹은 오른쪽 노드로 값을 넘겨주며 null에 도착할 때 까지 반복합니다.

null에 도착하면 그 공간에 값을 추가합니다.

public void add (E obj, Node<E> node){
		// 노드와 추가할 객체 비교
	if (((Comparable<E>) obj).compareTo(node.data) >=0){ 
		// 크면 오른쪽으로 이동
		if(node.right == null) { // 3
			node.right = new Node<E>(obj);
			return;
		}
		return add (obj, node.right); // 2
	}
	//  작으면 왼쪽으로 이동
	if(node.left == null) { // 3
		node.left = new Node<E>(obj);
		return;
	}
	return add (obj, node.left); // 2
}
// 트리가 비어있을 경우 (오버로딩)
public void add (E obj){
	if (root==null)
		root = newNode<E>(obj);
	else
		add(obj, root);
	currentSize++;
}

---

Conatins

특정 요소가 트리에 포함되어있는지를 확인해보겠습니다.

add와 유사하게 루트부터 시작해서, 트리 규칙에 따라 내려가면서 요소를 찾습니다.

요소를 찾으면 true를 반환하고, null에 도착하면 false를 반환합니다.

위 내용을 코드로 구현하면 다음과 같습니다.

public boolean contains (E obj, Node<E> node){
	// 트리의 끝에 도달했는데 null
	if (node==null)
		return false;
	// node의 data와 일치
	if (((Comparable<E>) obj).compareTo(node.data) == 0)
		return true;
	// go to the right
	if (((Comparable<E>) obj).compareTo(node.data) > 0)
		return contains(obj, node.right);
	// go to the left
	return contains(obj, node.left);
}

---

remove

힙에서는 요소를 제거할 때 루트에 있는 값을 꺼내고 다른 요소와 비교하면서 자리를 바꾸었습니다.
하지만 이진트리에서는 이 방법이 불가능합니다.

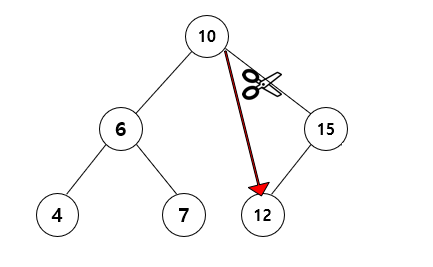
1) 잎 노드 (자식노드가 없는 노드) 제거

트리는 left, right, parent의 포인터를 가지고 있습니다.

이 포인터의 연결을 끊으면 가비지 컬렉션의 대상이 되어 제거할 수 있습니다.
(위 그림에선 right 포인터 )

즉, 부모노드의 포인터를 null로 설정하면 됩니다.

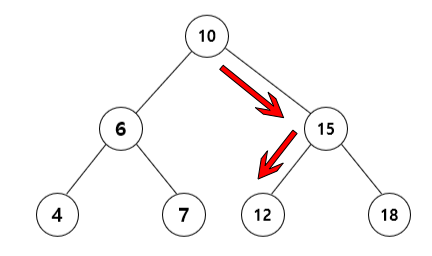
2) 자식노드가 하나인 노드 제거

부모노드의 포인터를 자식노드로 향하게하면 됩니다.

위 그림에서는 15 노드를 제거하기 위해서 부모노드의 포인터를 15노드의 자식노드인 12번을 가르키게 했습니다.

주의해야할 점은 부모노드에서 사용했던 포인터와 같은 포인터가 자식노드로 향하게 해야합니다.

3) 자식노드가 두개인 노드 제거

이 노드를 제거하기 위해선 중위 후속자와 중위 선임자에 대해 알아야합니다.

중위 후속자(in order successor)
제거하고자 하는 노드에서 시작하여 왼쪽으로 한 번 내려갔다가 계속 오른쪽으로 내려간 곳의 잎 노드입니다.

중위 후속자는 제거하고자 하는 노드보다 작은 노드들 중에서 가장 큰 노드입니다.

(중위 순회 방식으로 노드를 탐색할 때 루트 노드를 방문하기 직전에 만나게 되는 노드이기 때문에 중위 후속자라고 부릅니다.)

중위 선임자(in order predessor)
제거하고자 하는 노드에서 시작하여 오른쪽으로 한 번 내려갔다가 계속 왼쪽으로 내려간 곳의 잎 노드입니다.

중위 선임자는 제거하고자 하는 노드보다 큰 노드들 중에서 가장 작은 노드입니다.

이렇게 구한 중위 후속자와 중위 선임자는 모두 잎 노드입니다.

제거하고자 하는 노드를 중위 후속자와 중위 선임자 중 하나와 자리를 바꾼후 잎 노드를 제거하면 됩니다.