트리 - 순회

트리의 노드를 방문하는 방법을 트리 순회라고 합니다.

트리 순회

전위 순회 (Pre order traversal): 루트 노드에서 시작하여 왼쪽 자식 노드에 갔다가 오른쪽 자식 노드로 가는 순회 방법입니다.
다른 모든 노드를 지나기 전에 루트 노드를 방문하기 때문에 이름에 전(Pre)이 들어갑니다.

중위 순회 (In order traversal): 왼쪽 자식 노드에서 시작하여 루트 노드에 갔다가 오른쪽 자식 노드로 가는 순회 방법입니다.

후위 순회 (Post order traversal): 왼쪽 자식 노드에서 시작하여 오른쪽 자식 노드에 갔다가 루트 노드로 가는 순회 방법입니다.

너비 우선 선회/레벨 순서 순회 (Breadth first traversal/level order traversal): 가장 위에 있는 노드에서 시작하여 왼쪽에서 오른쪽으로 가는 순회 방법입니다.

표현식 트리

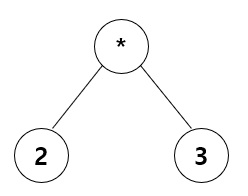
위와 같은 트리를 순회해보겠습니다.

• 중위순회 : 왼쪽 노드 -> 루트 -> 오른쪽 노드 순서로 순회하면 2 * 3 입니다.

• 전위순회 : 루트 -> 왼쪽 노드 -> 오른쪽 노드 순서로 순회하면 * 2 3 입니다.

• 후위순회 : 왼쪽 노드 -> 오른쪽 노드 -> 루트 순서로 순회하면 2 3 * 입니다.

위 처럼 표현식 트리를 사용해 복잡한 중위식을 후위식으로 간단하게 나타낼 수 있습니다.

예시를 하나 더 들어보겠습니다.

위 트리를 표현식을 작성하면 다음과 같습니다.

중위 표기식: $(((22 / 11) + 3) * (6 + 5)) - 50$
후위 표기식: $22 11 / 3 + 6 5 + * 50 -$

위처럼 후위 표기식은 중위 표기식과 달리 괄호와 연산자의 우선순위를 고려하지 않고 왼쪽부터 차례대로 계산할 수 있기 때문에 훨씬 간편한 표현방법입니다.