Backprop with tensors

미분을 구조적으로 어떻게 구현했는지 살펴보았습니다. 지금까지는 scala값으로 미분했으나, vector 혹은 matrix 형태가 들어오면 어떻게 처리하는지 알아보겠습니다.

Recap: Vector Derivatives

input: scala, output: scala -> 미분(dericative)
input: vector, output: scala -> gradient
input: vector, output: vector -> jacobian

Jacobian?

함수의 입출력도 각각 여러 개인 경우, 각각의 입력 변수가 각각의 출력 변수에 얼마나 영향을 미치는지 계산한 결과를 행렬로 만들어 놓은 것이 Jacobian입니다.

Example: Matrix Multiplication

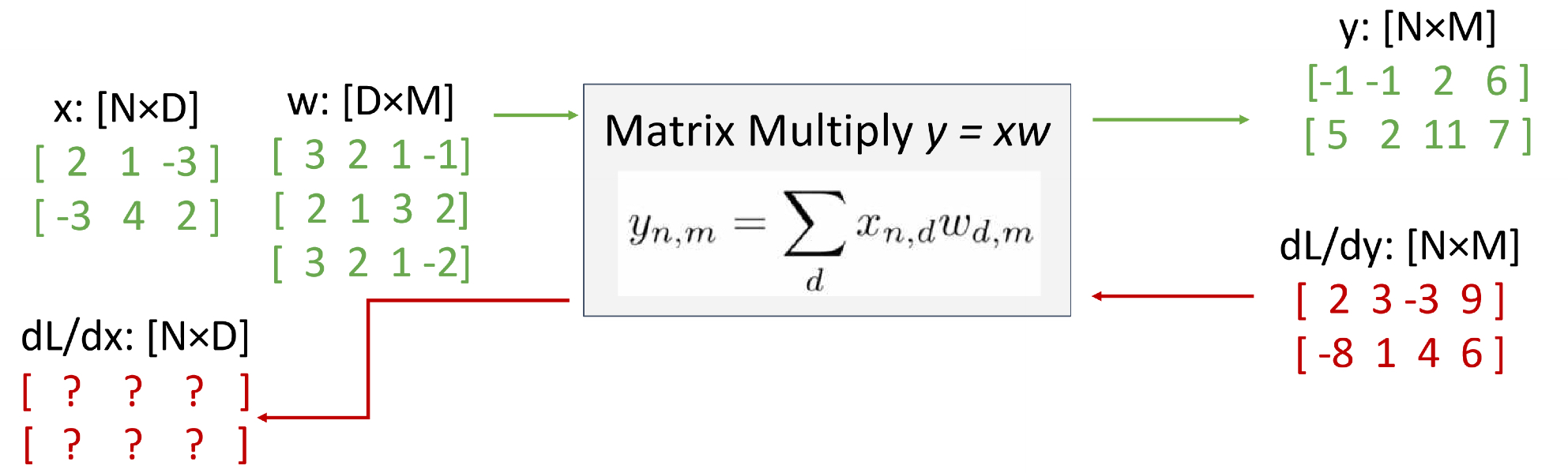
1. dL/dx가 downstream gradient, dL/dy가 upstream gradient이므로, local gradient를 구해야 합니다. 즉, localstream gradient는 dy/dx이므로, 각각의 자리에서 y에 대한 x의 미분을 진행해야 합니다.
1-1. $y_{1,1}$ 자리를 구하겠습니다. $y_{1,1} = x_{1,1}w_{1,1} + x_{1,2}w_{2,1} + x_{1,3}w_{3,1}$를 $x_{1,1}$로 미분 -> $y_{1,1} = w_{1,1} = 3$
1-2. $y_{1,2}$, $y_{1,3}$, $y_{1,4}$, $y_{2,1}$, $y_{2,2}$, $y_{2,3}$, $y_{2,4}$ 모두 1-1과 같은 방식으로 진행 시, 다음과 같은 결과가 나옵니다.

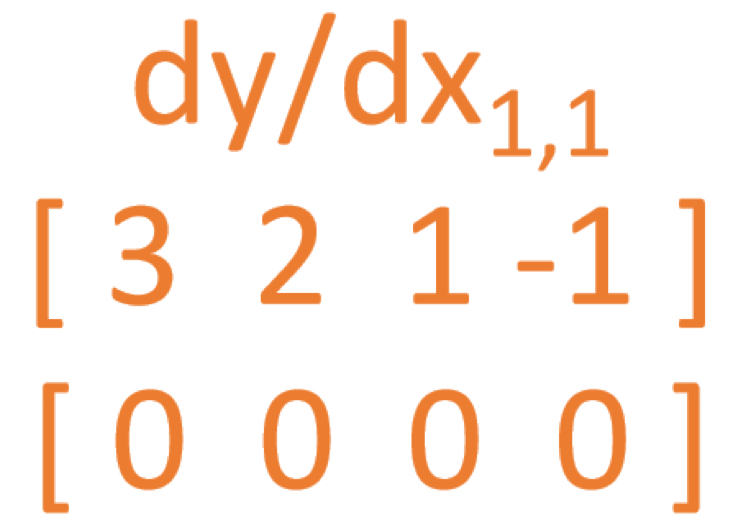
2. downstream gradient = localstream gradient * upstream gradient 식을 기반으로 $dL/dx_{1,1}$의 값을 구합니다. 내적을 이용하여 구합니다.
2-1. 3*2 + 2*3 + 1*(-3) + (-1)*9 = 0 (dy/dx의 2행이 모두 0이므로 2행은 계산할 필요가 없습니다.)
3. $dL/dx$의 다른 자리도 반복하여 구합니다.

해당 과정을 일반화하면 아래와 같은 식이 나오게 됩니다.

$dL/dx = (dL/dy)w^T$ 또는 $dL/dw = (dL/dy)x^T$