Lecture 7: Convolutional Neural Networks
이번에는 CNN에 대해 살펴보고자 합니다. Fully-Connected NN과는 어떻게 다른지, 어떤 특징을 가지고, 어떤 데이터에 적합한지 등에 대해 공부해보겠습니다.
이전에는 neural network를 학습시킬 때, 어떻게 gradient를 계산할 것인지를 알아보았습니다. 첫 번째로 forward로 연산을 진행한 후, backward으로 gradient를 계산합니다. 이때 Downstream gradient = Upstream gradient * Localstream gradient라는 식을 이용하여 gradient를 계산하며 내려옵니다.
하지만 Fully-Connected Network은 이미지의 공간적 구조를 무시하게 됩니다. 따라서 해당 문제를 해결할 방법으로 CNN를 사용하게 됩니다.
Components of a Fully-Connected Network
Fully-Connected Network에는 Fully-Connected Layer와 Activation Function이 필요합니다.
- Fully-Connected Layer: hidden layer는 뉴런으로 이루어지고, 각 뉴런은 앞쪽 layer의 모든 뉴런과 연결됩니다.
- Activation Function: 비선형성을 도입하여 x의 다양한 변환을 표현합니다. (주로 ReLU 사용 추천)
Components of a Convolutional Network
Convolutional Network에는 Fully-Connected Layer와 Activation Function 뿐만 아니라 Convolution Layers, Pooling Layers, Normalization이 추가적으로 필요합니다.
- Convolution Layer: 이미지를 필터와 Convolution 연산을 통해 처리하여 특징 맵(Feature Map)을 생성합니다.
- Pooling Layer: 이미지를 다운샘플링하여 크기를 줄이는 역할입니다. Pooling은 가중치나 바이어스를 학습하지 않고, 파라미터가 없습니다.
Normalization: 데이터를 일정한 범위나 분포로 변환하여 모델 학습을 더 효과적으로 만드는 과정입니다.
Convolutional Network에서 가장 중요한 Convolution Layers부터 살펴보겠습니다.
Fully-Connected Layer
이전에 공부했던 Fully-Connected Layer를 다시 살펴봐야 합니다.
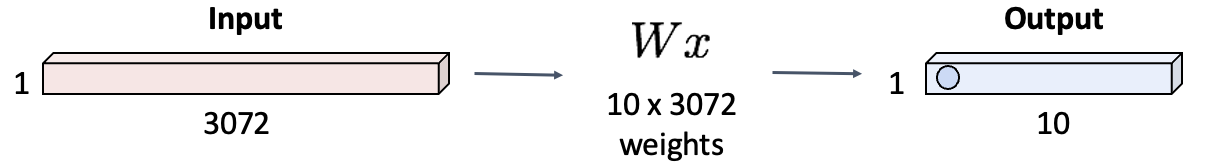
Fully-Connected Layer에서는 input 이미지 데이터(x)를 벡터 형태로 펴줍니다. W는 10x3072 사이즈의 weight matrix이고, matrix-vector 곱셈(내적)을 진행하면 10x1의 벡터가 나옵니다.
이처럼 x를 벡터로 펼치면서 이미지 픽셀들의 공간적 정보가 무시되었습니다.
Convolution Layer
이미지의 공간적 정보가 무시되는 Fully-Connected Layer와 달리, Convolution Layer는 공간적 구조를 보존하면서 이미지를 처리하여 이미지 데이터셋에 적합합니다.
Convolution Layer는 필터를 이미지와 Convolve합니다. 내적곱을 진행하면서 필터를 슬라이딩시키는 방식입니다.

즉, filter W는 이미지 위를 슬라이딩하며 그대로 한 칸씩 움직이고, x는 변하면서 내적합니다. 이 과정의 결과로 새로운 Activation Map이 생성되고, 필터 수에 따라 여러 개의 Activation Map이 쌓입니다.
예시를 통해 더 자세히 알아보겠습니다.
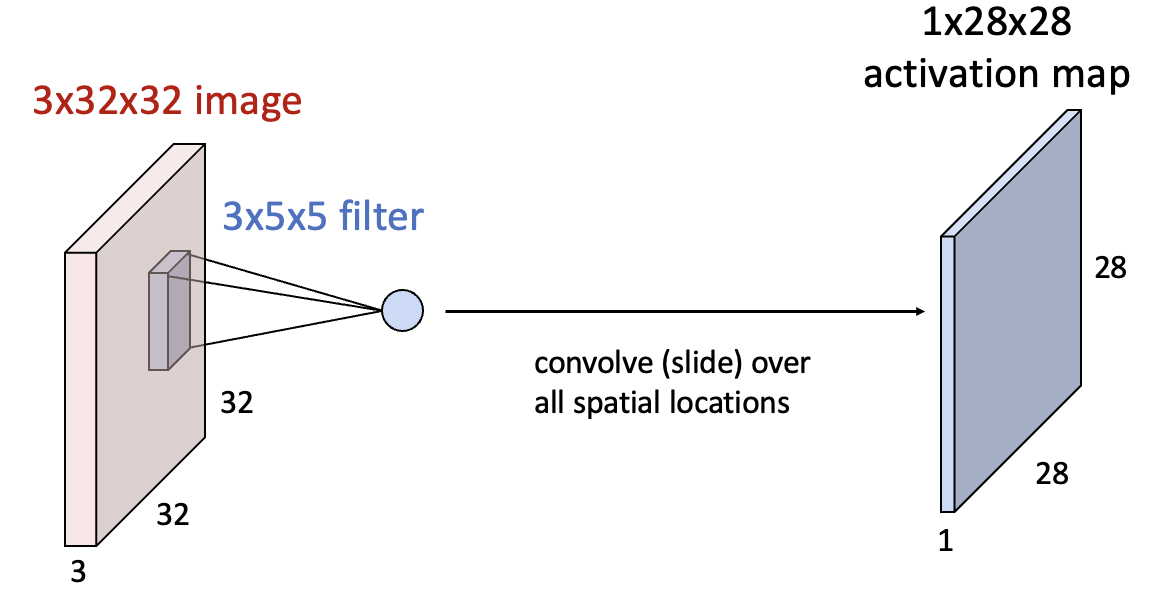
이미지의 일부와 필터의 내적을 하면 scala 값이 나옵니다. 따라서 3x32x32의 input 이미지에 필터를 Convolve하면 1x28x28의 결과가 나옵니다.
 또 다른 필터로 같은 일을 반복하면 새로운 1x28x28 크기의 Activation Map이 생성됩니다. 즉, filter는 여러 개일 수 있습니다.
또 다른 필터로 같은 일을 반복하면 새로운 1x28x28 크기의 Activation Map이 생성됩니다. 즉, filter는 여러 개일 수 있습니다.input 이미지가 3x32x32이고, 필터의 크기가 3x5x5로 총 6개이므로 6x3x5x5입니다.
Convolution Layer의 각 뉴런은 input 이미지의 filter의 weight를 가해줍니다. 그 결과 6x28x28의 Activation Map이 나옵니다.
이미지와 필터의 weight를 내적한 후, 6개의 bias을 더해줍니다.
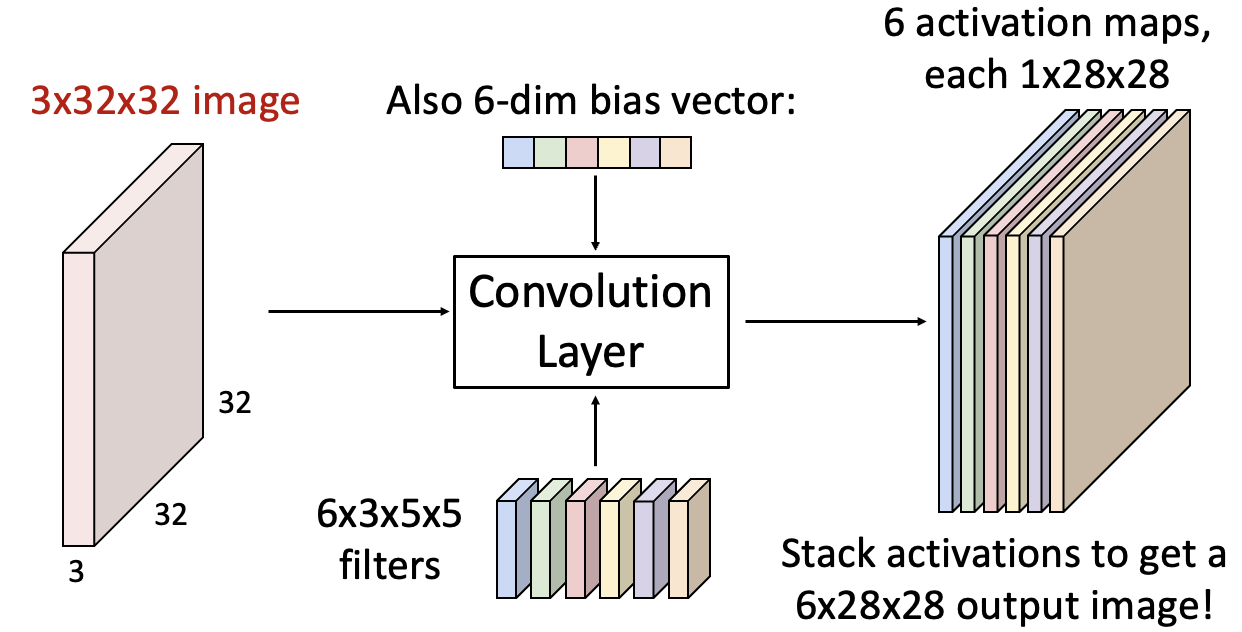
이렇게 계산해낸 output 이미지를 해석하는 방법은 두 가지가 있습니다.
1. 6개의 Activation Map
2. 총 6차원으로 이루어진 28x28 사이즈의 grid -> input 이미지의 5x5(필터 크기) 영역에서 추출된 6차원의 feature들의 모음 (각 grid에 feature 6개 대응)
input 이미지가 여러 개인 경우를 살펴보겠습니다.
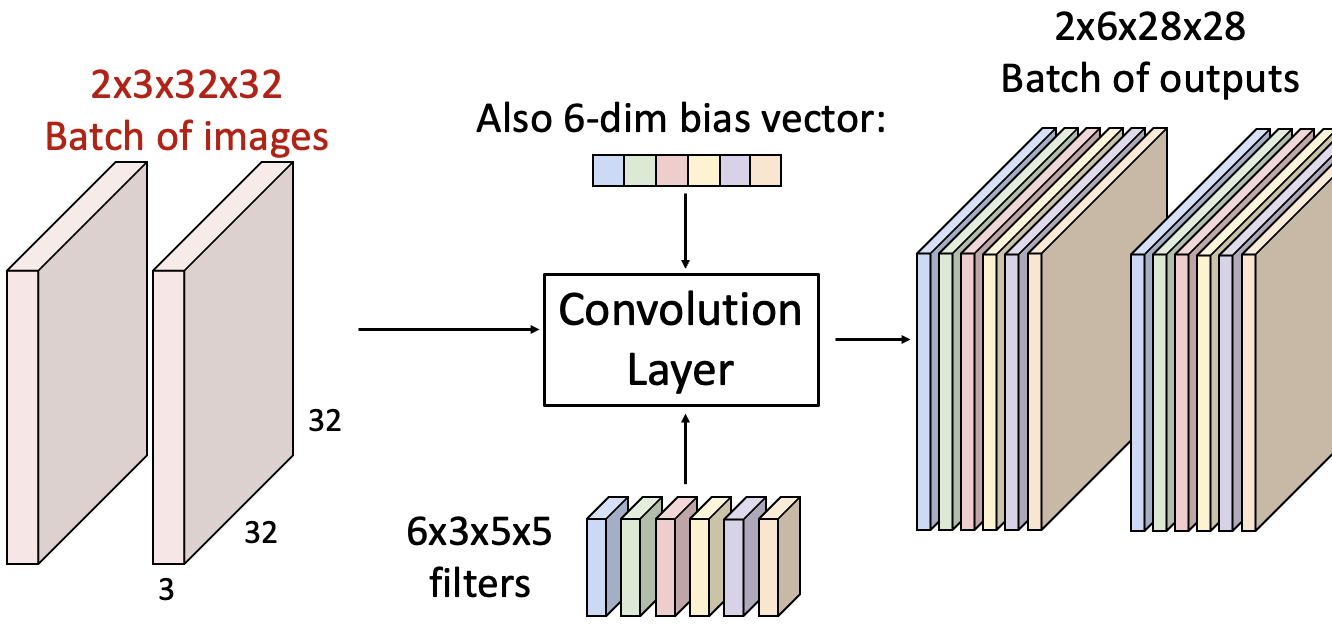
input이 2x3x32x32, filter가 6x3x5x5이면 output은 2x6x28x28이 됩니다. 즉, 일반화하면 다음과 같습니다. (H', W'는 뒤에서 계산하는 방법을 설명할 예정입니다.)
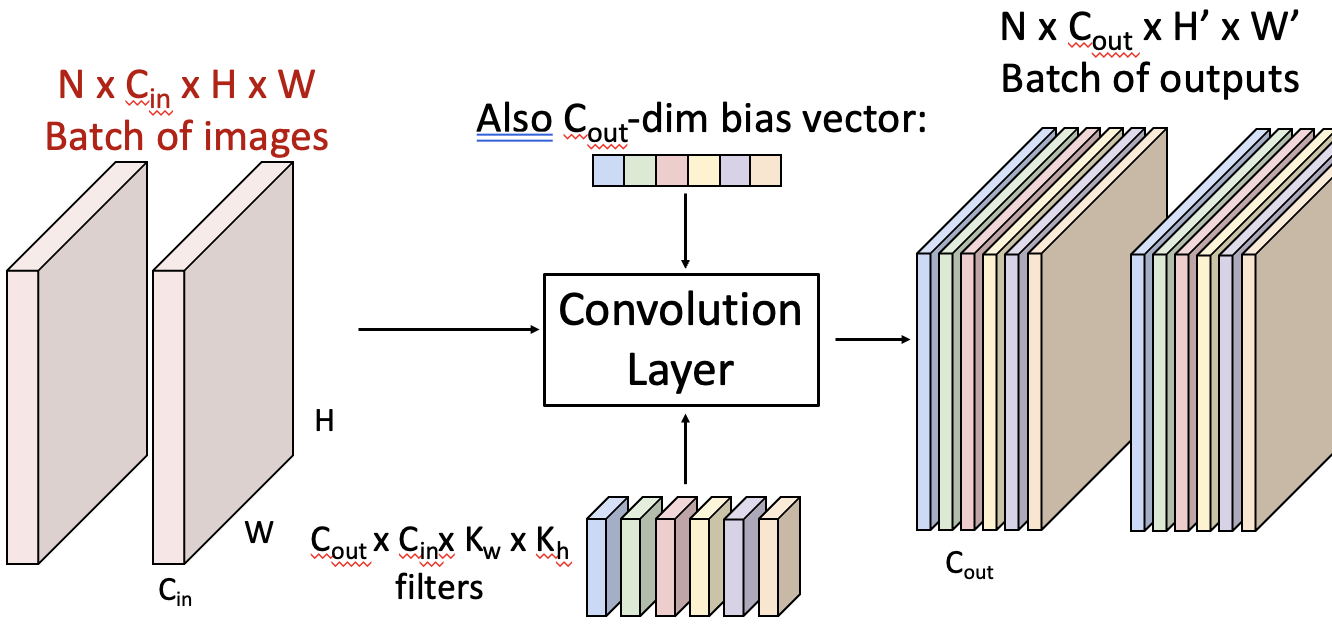
Stacking Convolutions
Convolutional Network를 만들기 위해 Convolutional Layer를 여러 개 쌓는 구조에 대해 알아보겠습니다.
Convolve 레이어를 하나 먹이면 28x28 Activation Map이 6개(필터 개수), 또 먹이면 10개가 나옵니다(최종 결과는 총 10개).
이때 Convolve 레이어를 먹이는 연산은 한 픽셀만 보는 것이 아니라 주변 픽셀까지 함께 고려해 픽셀별 의존성이 반영된 상태로, 이 특징은 Fully-Connected와의 차이점입니다. 그러나 이 연산 자체는 linear하므로, ReLU를 Convolutional Layer의 output 텐서에 적용합니다.
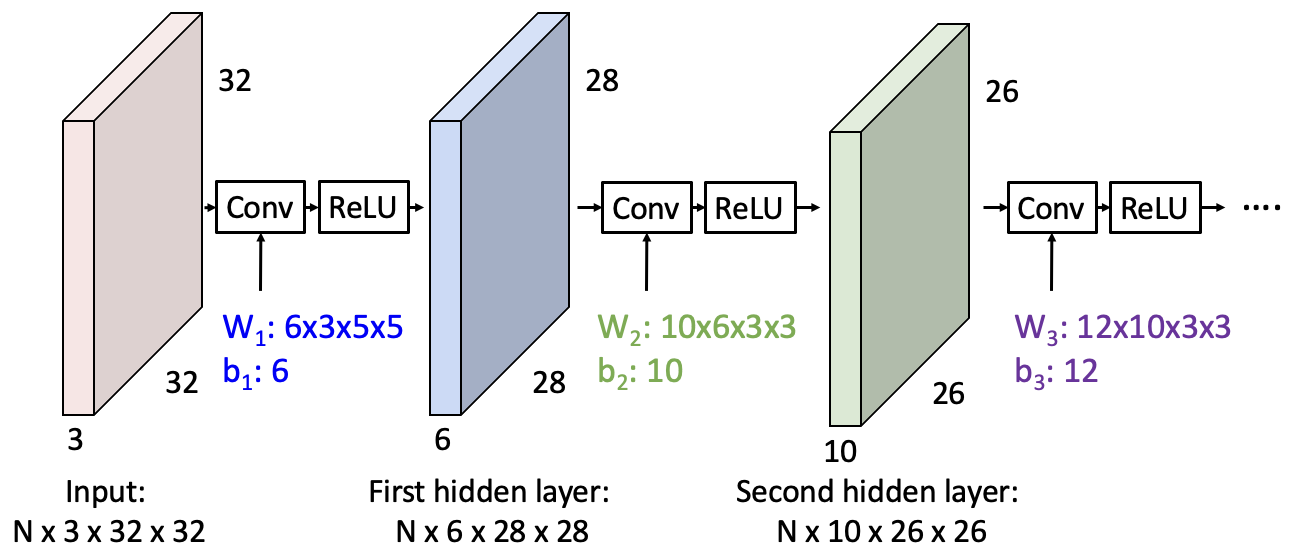
따라서 Convolutional Layer에 ReLU Activation Function을 먹임으로써 전체적으로는 nonlinear transform이 됩니다.
What do convolutional filters learn?
그렇다면 하나의 Convolutional Filter는 무엇을 학습하는 것일까요?
6x3x5x5 필터, 즉 6개의 3x5x5 사이즈의 이미지를 만들어낼 수 있습니다. 이는 Linear classifier에서의 템플릿과 비슷합니다.
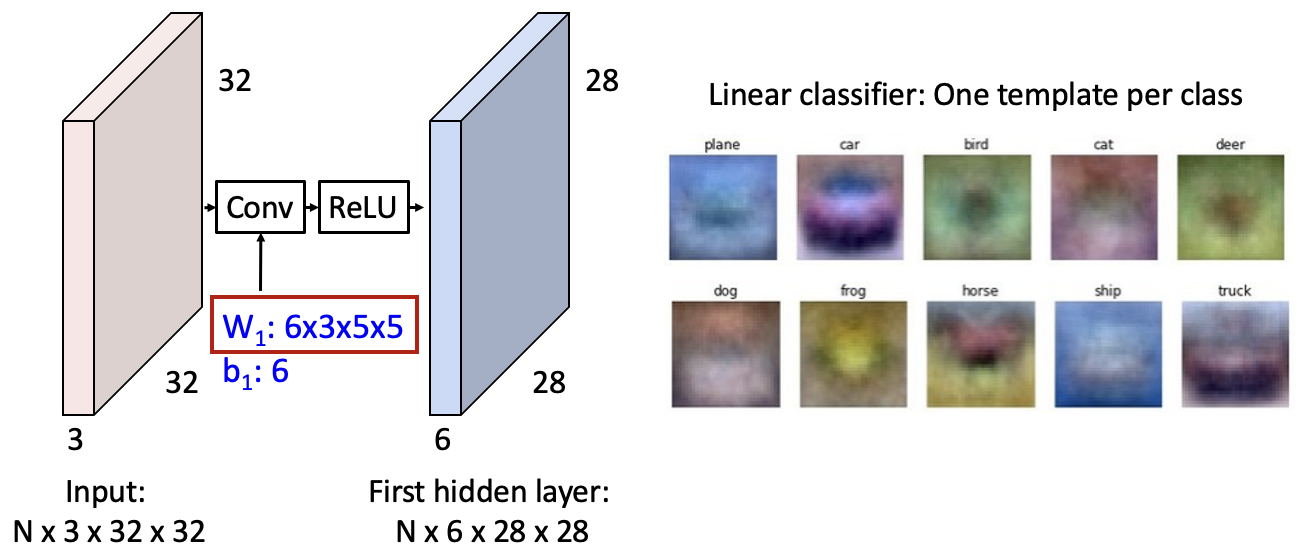
alexnet(CNN 모델)에서 64개의 필터를 이미지화했는데, input 이미지의 edge를 highlight하는 모양으로 생겼습니다. 즉, 학습된 filter들이 edge부분이 증폭되어 activation map이 계산될 수 있도록, 이미지의 edge들을 추출하는 feature extractor(추출기)의 역할을 할 것입니다. 이는 실제 이미지의 보색으로 이루어지기도 합니다.
결과적으로, convolution filter는 학습을 하면서 low level feature(이미지의 선, 엣지 등)를 조합해서, high level feature(자동차, 고양이 등 구체적인 객체나 형태)를 형성합니다.
A closer look at spatial dimensions
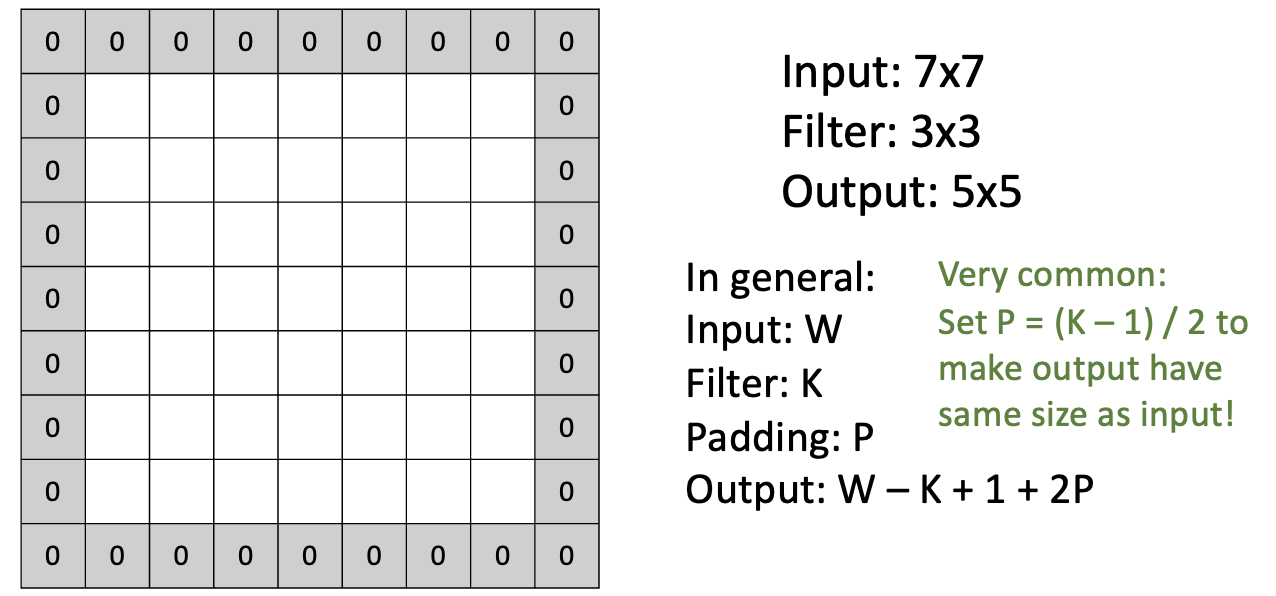
input 이미지(W)의 크기는 7x7, 필터(K)의 크기는 3x3으로 보고, 이미지와 내적을 하면서 필터를 한 칸씩 이동시킬 수 있습니다. 한 칸씩 이동을 하면서, output의 사이즈는 W-K+1로 자동적으로 결정됩니다.
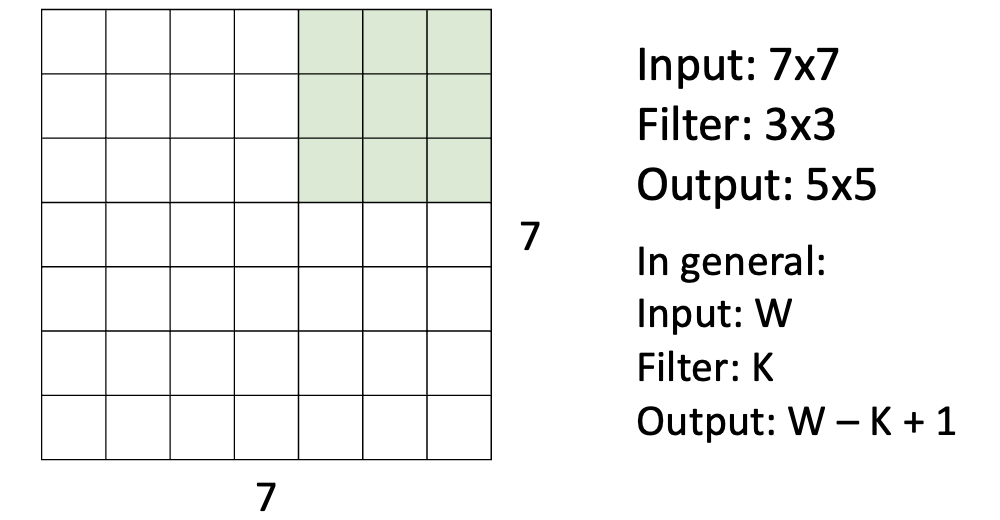
이때, 이미지 사이즈가 줄어드는 단점이 있습니다. 결과적으로 표현되는 픽셀 수가 줄어들어, 다양한 패턴들이 줄어드는 문제가 생깁니다.
Activation map의 사이즈가 계속 줄어드는 단점을 해결하기 위한 방안으로는 Padding이 있습니다. Padding이란 input 이미지 주변에 0 픽셀을 두르는 것입니다. Padding은 주로 input과 같은 크기의 output을 내기 위해, (K-1)/2로 패딩값을 정합니다. Padding이 있다면 output의 사이즈는 W-K+1+2P로 변경됩니다.
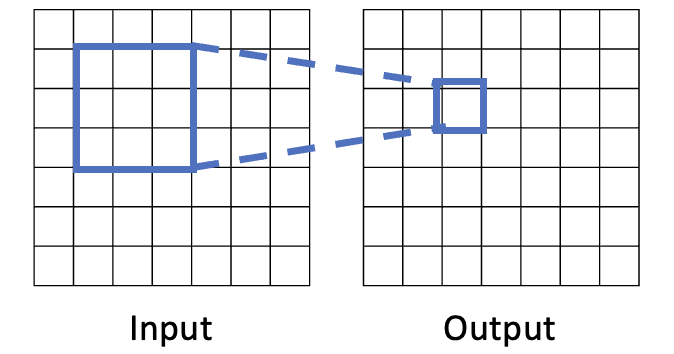
Receptive Fields
3x3 필터를 먹이면, 다음 레이어의 한 칸에 대응됩니다. 이때 이 한 칸을 생성하기 위해서, 필터가 적용된 영역을 receptive field라고 합니다.
Conv 연산 3번 전까지 가면, 해당 한 칸의 리셉티브 필드는 input 이미지 픽셀 전체가 됩니다. 즉, Conv 레이어를 여러 번 쌓음으로써, 윗단 레이어의 각각의 픽셀들은 이미지 전체를 보고 처리한 결과일 수 있습니다.
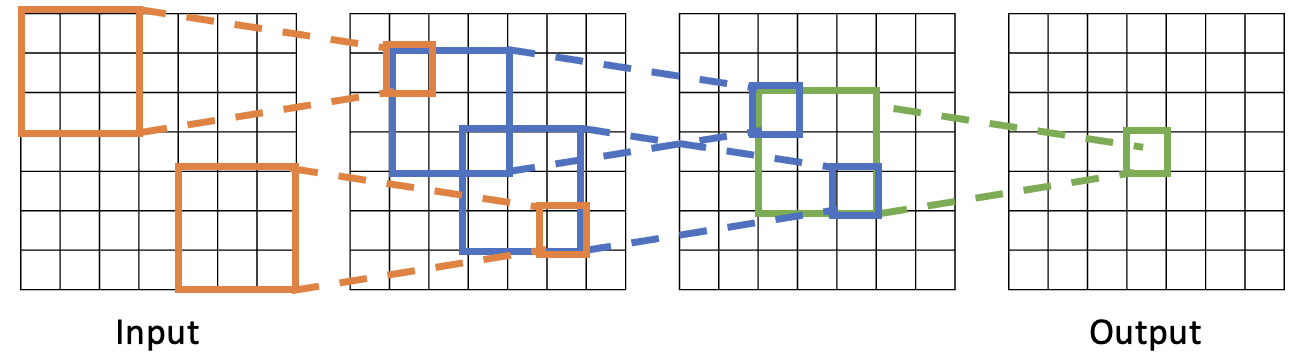
문제는 input 이미지가 커질수록 가장 상단 레이어(output에 가까운 레이어)에서 전체 이미지에 대한 정보를 수집하는데 필요한 레이어 수가 많아집니다. (Receptive Field의 크기는 레이어가 증가함에 따라 커집니다.)
따라서 Receptive Field를 넓게 가져가는 다른 방법이 필요합니다.
Strided Convolution
Receptive Field를 넓게 가져가기 위해 layer 개수를 조절하는 방법 외에, convolution에 Stride를 도입하는 방법이 있습니다.
Stride란 필터가 이동하는 간격입니다. Stride가 클수록 output 크기는 작아집니다. Strideg이 있다면 output의 사이즈는 {(W-K+2P)/S}+1로 변경됩니다.
W는 input, K는 filter, P는 padding, S는 stride일 때, 최종 output 크기 계산식은 다음과 같습니다.
{(W-K+2P)/S}+1 (답은 nxn의 형태)
Convolution Example
예시로 살펴보겠습니다.
Input: 3x32x32
필터: 10x3x5x5
Stride: 1
Padding: 2 (각 변에 2칸씩 0으로 채움)
Output 크기는 {(W-K+2P)/S}+1로 정의되므로,
가로: {(32-5+2*2)/1}+1 = 32
세로: {(32-5+2*2)/1}+1 = 32
즉, Output의 크기는 10x32x32 입니다. (10은 필터의 개수)
해당 예시에서 training data set에서 learnable parameter로는 무엇이 있을까요? Weight에 대응되는 개념은 필터이기 때문에, 필터의 크기를 살펴보겠습니다.
필터의 크기는 3x5x5이고, 각 필터는 3×5×5개의 가중치를 가집니다. 이 가중치 외에도 각 필터에는 bias가 1개씩 포함됩니다. 따라서 필터 하나당 파라미터 개수는 3*5*5 + 1 = 76입니다. 그리고 필터가 총 10개이므로, Learnble parameter의 개수는 10*76 = 760개입니다.
각 필터 하나와 필터에 대응하는 input 데이터 볼륨의 내적 연산을 통해 output을 계산합니다. 따라서 한 번의 연산에서 필요한 곱셈과 덧셈 연산 수는 75번입니다. (3×5×5 = 75) 이때 output이 10,240개이므로, 총 연산 수는 75 × 10,240 = 768,000번의 곱셈-덧셈 연산이 필요합니다.
파라미터 개수={(필터 크기 * 입력 채널) + 1(bias)} * 필터 개수
참고사항
필터 및 스트라이드가 커질수록, 그리고 패딩이 부족할수록(단순히 작은 것이 아닌 부족!) output 값이 축소됩니다. 필터 크기가 커지면 한 번에 처리하는 정보가 많아지므로, 스트라이드가 커지면 필터가 이동하는 거리가 멀어지므로 한 번에 처리하는 영역이 커져서, 패딩이 부족하면 입력의 가장자리가 손실되기 때문에 output 크기가 줄어듭니다.
레이어가 깊어질수록 Receptive Field의 크기는 증가하고, 더 많은 입력 정보에 접근할 수 있게 됩니다. Receptive Field는 각 레이어를 거치면서 점점 넓어지기 때문에 여러 레이어를 지나면서 더 넓은 영역의 입력 데이터를 볼 수 있게 됩니다.
CNN의 장점은 이미지의 중요한 패턴(예: 가장자리, 색상 대비)을 학습하고, 이미지의 위치 변화에도 강건합니다.
CNN에서 다중 필터를 사용하는 이유는, 다중 필터는 서로 다른 특징(예: 에지, 텍스처 등)을 학습할 수 있게 하여 모델의 표현력을 높입니다.
