Backpropagation with Computational graph

Problem: How to compute gradients?

이번에는 neural network를 학습시킬 때 어떻게 gradient를 계산하는지에 대해 살펴보겠습니다.

Nonlinear score function
$s = f(x; W_1, W_2) = W_2max(0, W_1x)$

Hinge Loss on predictions: $L_i$는 loss이며, $s_{y_i}$는 정답 output입니다. 따라서 $s_j - s_{y_i}$의 값이 커질수록 loss는 커집니다.
$L_i = \sum_{j≠y_i} max(0, s_j - s_{y_i} + 1)$

Regularization
$R(W) = \sum_{k} W^2_k$

Total loss: data loss + regularization
$L = \frac{1}{N} \sum_{i=1}^{N} + λR(W_1) + λR(W_2)$

$\frac{∂L}{∂W_1}$, $\frac{∂L}{∂W_2}$을 계산할 수 있다면 $W_1$과 $W_2$를 배울 수 있습니다.

(Bad) Idea: Derive $∇wL$ on paper

손으로 gradient를 직접 계산하려고 하면 매우 많은 수식과 종이가 필요합니다. 따라서 아무리 복잡한 모델이 와도 컴퓨터가 계산할 수 있는 모듈을 만들고자 합니다. 이때 모듈 계산을 도와주는 것이 Computational Graph입니다.

Better Idea: Computational Graphs

Computational Graph란 간단한 연산을 그래프 형태로 나타냄으로써, 전체 미분을 계산하는 데에 도움을 줍니다.

앞선 식을 이용하여 $∇wL$를 구하려면 식이 아주 복잡해집니다. 따라서 해당 과정을 Computational Graphs로 표현합니다.
-> SVM loss 관련이므로 그림을 이해할 필요는 없음 (시험 범위 X)

Backpropagation: Simple Example

밑 그림은 함수값이 딱 1개로 정해져 있는 간단한 상황에서의 backpropagation입니다. 목표는 computational graph로 표현하여 f'(-2, 5, -4)를 계산하는 것입니다.

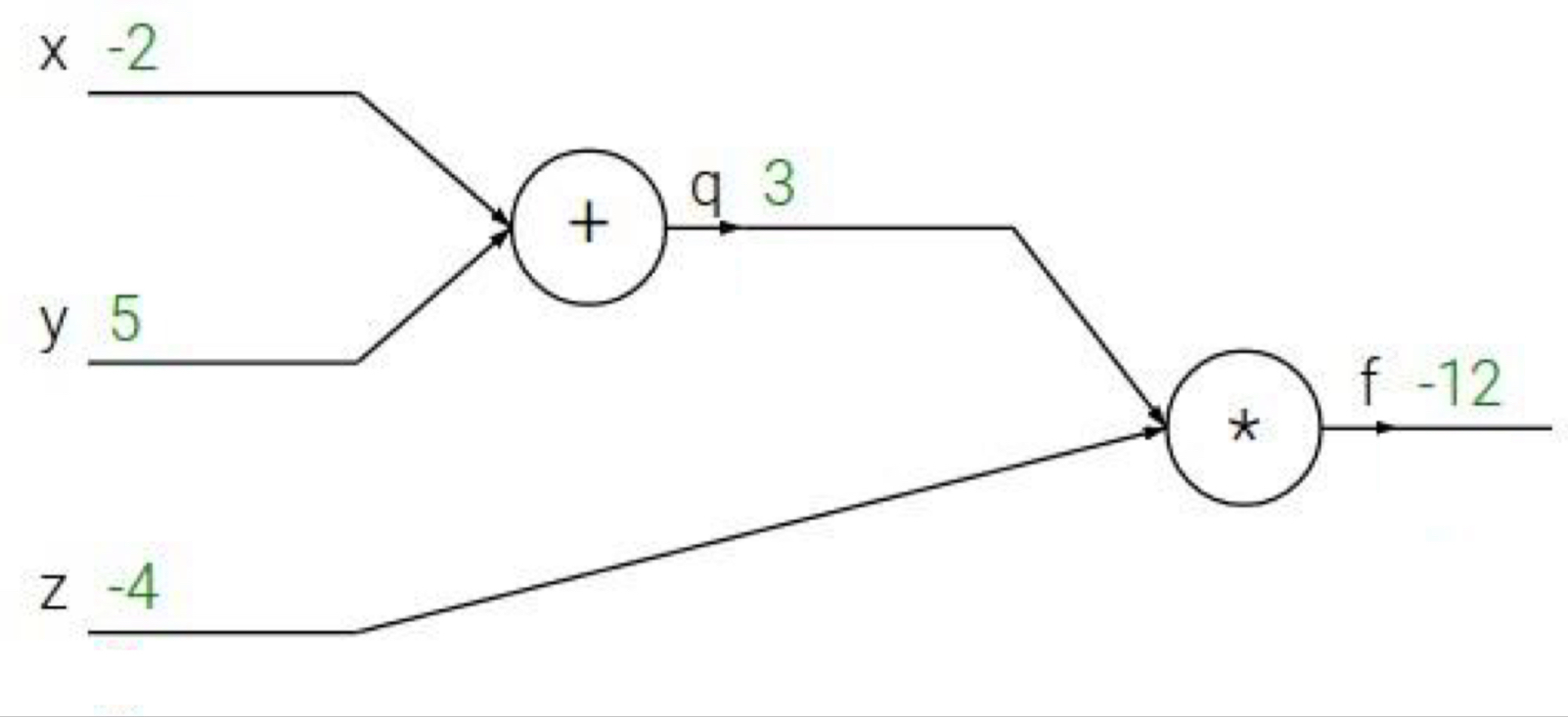
다음은 도함수를 계산하기 위한 단계입니다.
1. Forward pass: 모든 그래프 상에서 각 노드를 지난 연산 결과들을 써줍니다.
$q = x+y$
$f = qz$

2. Backward pass: 오른쪽에서부터 미분(derivative)값을 계산합니다.
   $\frac{∂f}{∂x}, \frac{∂f}{∂y}, \frac{∂f}{∂z}$
   2-1. 초깃값을 설정합니다. f를 f로 미분한 값인 1입니다.
   2-2. f를 z에 대해 편미분합니다. f=qz입니다.
   $\frac{∂f}{∂z} = \frac{∂qz}{∂z} = q = 3$
   2-3. f를 q에 대해 편미분합니다.
   $\frac{∂f}{∂q} = \frac{∂qz}{∂q} = z = -4$
   2-4. f를 y에 대해 편미분합니다. q=x+y입니다. (chain rule 적용)
   $\frac{∂f}{∂y} = \frac{∂q}{∂y} \times \frac{∂f}{∂q} = \frac{∂(x+y)}{∂x} \times \frac{∂f}{∂q} = 1 \times -4 = -4$
   2-5. f를 x에 대해 편미분합니다. (chain rule 적용)
   $\frac{∂f}{∂x} = \frac{∂q}{∂x} \times \frac{∂f}{∂q} = \frac{∂(x+y)}{∂x} \times \frac{∂f}{∂q} = 1 \times -4 = -4$

위에서 2-4와 2-5단계에서 chain rule에 의해 계산되는 식을 재정의하면 다음과 같습니다.

• Upstream gradient: 앞쪽 노드에 대한 그래디언트(이미 계산)
• Local gradient: 해당 노드 내에서만 계산되는 그래디언트
• Downstream gradient: 노드 input 자리에 있는 변수에 대한 그래디언트

즉, Downstream gradient = Local gradient * Upstream gradient입니다.

이처럼 input, 연산 노드, output를 가지고 있는 심플한 구조를 활용하여 gradient를 순차적으로 계산할 수 있습니다.

과정

1. forward pass: f라는 연산 노드에 input인 x와 y를 넣어서 f(x,y)=z를 계산합니다.
2. backward pass: 맨 끝 노드에서부터 gradient를 역방향으로 계산해옵니다. f 노드 방향으로 Upstream gradient가 들어옵니다.
3. z = f(x,y)를 이용해서, local gradient를 계산합니다.
4. Downstream gradient에 대해서 Local gradient와 Upstream gradient를 chain rule로 접하여 계산할 수 있습니다.

즉, forward pass는 함숫값, backward pass는 미분값으로 볼 수 있습니다.

Gradients of other Activation Functions?

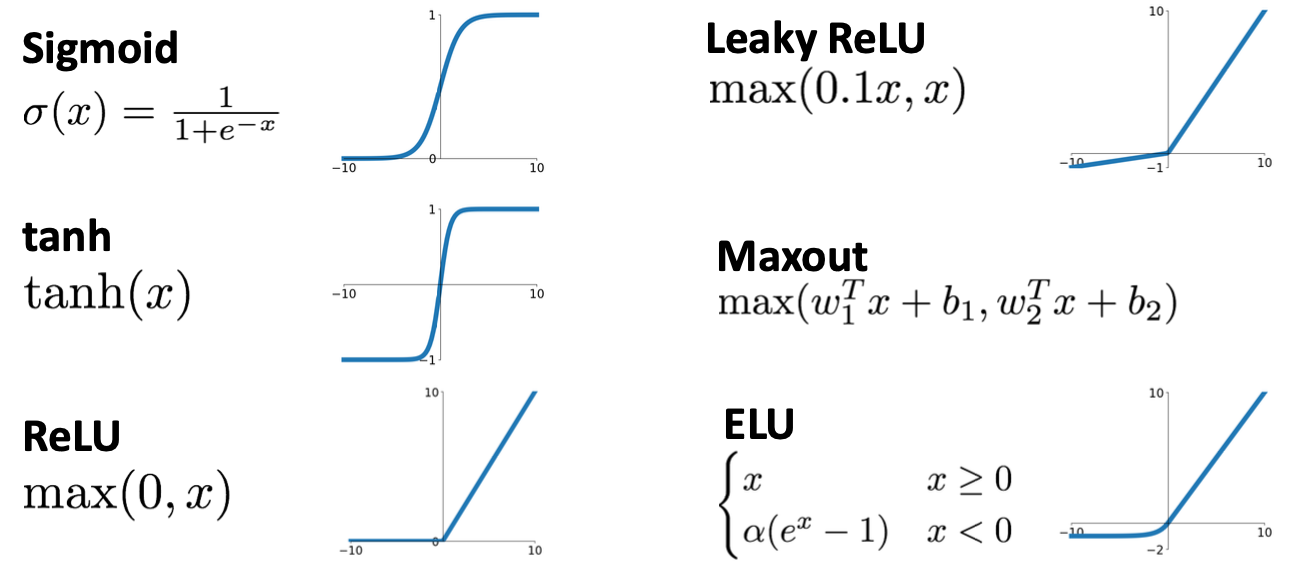
Gradients of activation functions?

Cross-Entropy Loss (Multinomial Logistic Regression)

Gradients of softmax?

Patterns in Gradient Flow

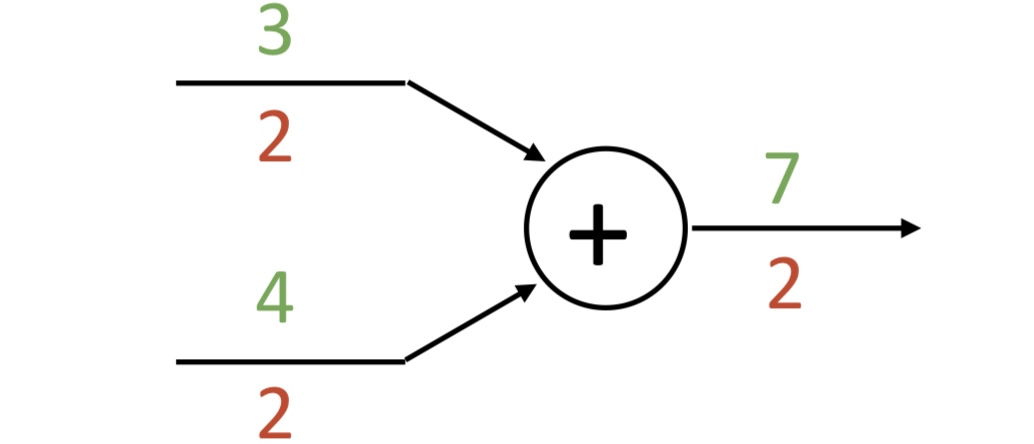
add gate: gradient distributor

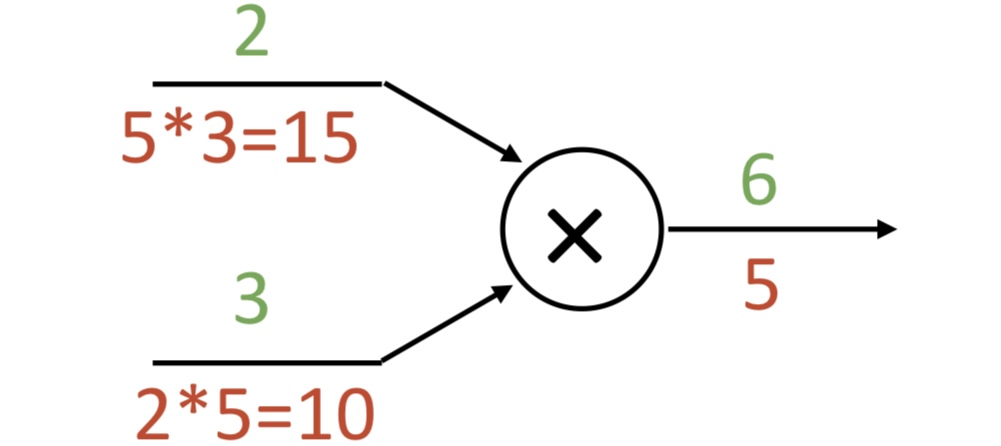
mul gate: “swap multiplier”

max gate: gradient router

Backprop Implementation: ”Flat” gradient code: -> 여기만 하기

앞서 본 것과 같이, backprop 과정은 코드로도 간단하게 구현할 수 있다. 다시 sigmoid를 계산하는 식을 보자. 우선, 함숫값들을 forward pass로 계산한.

Gate의 원리를 이용하여 backward pass를 구현해보자.
L에서 멀어져가는 방향으로 거꾸로 흘러간다.
grad_s3는 $\frac{∂L}{∂S_3}$를 나타낸다(just naming convention)

grad_L은 초기 gradient로 1로 설정.

grad_s3 : [Local] * [Upstream]

grad_w2, grad_s2
: s3가 add gate이므로, upstream gradient값을 전달해주기만 하면 된다.
즉, grad_w2 = [Upstream], grad_s2=[Upstream]

grad_s0, grad_s1
: s2가 add gate이므로, upstream gradient값을 전달해주기만 하면 된다.
즉, grad_s0= [Upstream], grad_s1=[Upstream]

grad_w1, grad_x1
: s1이 mul gate이므로, 각각의 local gradient는 w1과 x1값을 서로 switch해주기만 하면 된다.
즉, grad_w1 = [Local] [Upstream] = x1 [Upstream]
grad_x1 = [Local][Upstream] = w1 [Upstream]

grad_w0, grad_x0
: s0이 mul gate이므로, 각각의 local gradient는 w0과 x0값을 서로 switch해주기만 하면 된다.
즉, grad_w0 = [Local] [Upstream] = x0 [Upstream]
grad_x0 = [Local][Upstream] = w0 [Upstream]

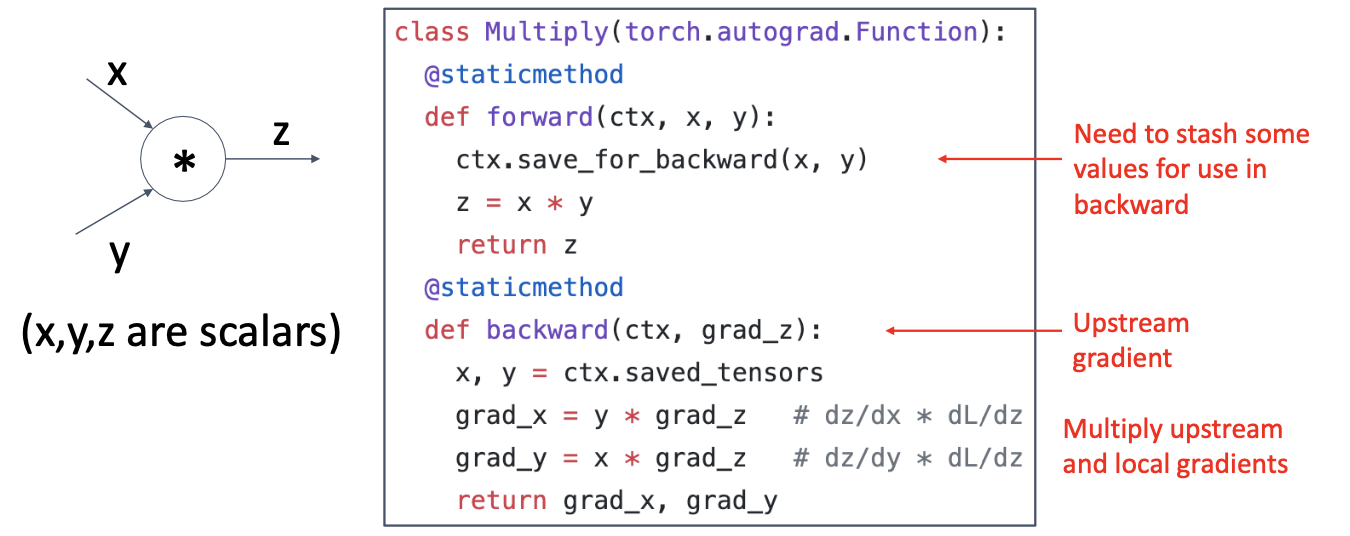
Example: PyTorch Autograd Functions

이미 pytorch에서 연산에 대해 구현해놓은 모듈들이 존재합니다. 예시는 multiply gate에 대해 forward 과정, backward 과정을 구현해 둔 코드입니다.