Regularization

해담·2024년 11월 28일
컴퓨터비전

컴퓨터비전

목록 보기
9/13

Overfitting

Overfitting이란 모델이 training data에만 과도하게 맞춰진 현상을 뜻합니다. overfitting된 모델은 training data에 매우 잘 맞을 수 있지만, 새로운 예제(test 또는 validation data)에서는 성능이 저하됩니다.

One concern

Loss Function 계산 관련하여, training data에서 손실을 최소화하는 가중치 W와 절편 b가 항상 테스트 데이터에서도 최적이라고 할 수는 없습니다.

L=1N∑iLi(f(xi,W),yi)L = \frac{1}{N} \sum_{i} L_i(f(x_i, W), y_i)

따라서 overfitting을 방지하기 위한 Regularization와 같은 추가적인 기법이 필요합니다.

Overfitting revisited: regularization

regularization는 모델이 training data에 과도하게 맞춰지지 않도록 loss function에 추가 기준을 더하는 과정입니다. 매개 변수를 더 normal하고 regular하게 유지하려고 하기 때문에 regularization이라고 합니다.

Regularization: Beyond Training Error

L(W)=1N∑iLi(f(xi,W),yi)+λR(W)L(W) = \frac{1}{N} \sum_{i} L_i(f(x_i, W), y_i) + λR(W)
  • 첫 번째 항: Data loss 부분 -> training data와 모델의 예측이 잘 맞는지 평가합니다.
  • 두 번째 항: Regularization 부분 -> 모델이 training data에서 너무 잘 작동하지 않도록 패널티를 추가합니다.
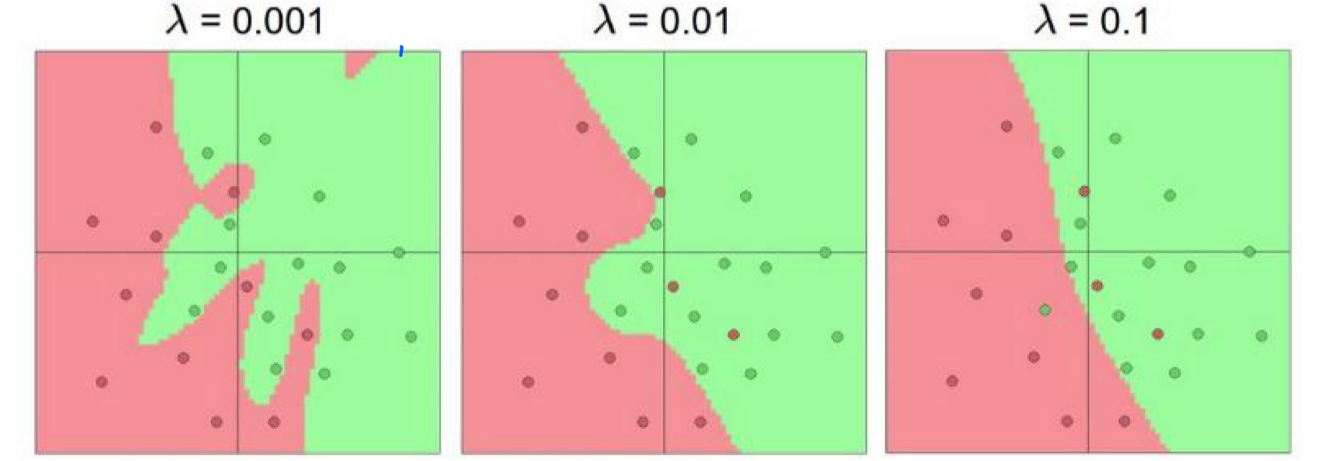
    • λ(람다): Regularization 강도를 조절하는 하이퍼파라미터로, 람다 값이 작을수록 Regularization의 영향을 덜 받음

Regularizers

f=Wxf = Wx

일반적으로 큰 weight(가중치)를 원하지 않습니다. 큰 weight는 작은 변화에도 측값을 크게 만들어 모델 안정성을 떨어뜨리기 때문입니다. 그렇다면 작은 weight를 어떻게 구해야 할까요?

Regularization: Beyond Training Error

Regularization의 예시는 다음과 같습니다.

Simple examples
L2 regularization: 모든 가중치의 제곱합을 페널티로 부과합니다. (ridge regression)

R(W)=∑k∑lWk,l2R(W) = \sum_{k} \sum_{l} W^2_{k,l}

L1 regularization: 모든 가중치의 절댓값 합을 페널티로 부과합니다. (lasso regression)

R(W)=∑k∑l∣Wk,l∣R(W) = \sum_{k} \sum_{l} |W_{k,l}|

Elastic net (L1 + L2): L1과 L2를 혼합한 방식입니다.

R(W)=∑k∑lβWk,l2+∣Wk,l∣R(W) = \sum_{k} \sum_{l} βW^2_{k,l} + |W_{k,l}|

More complex:
Dropout
Batch normalization
Cutout, Mixup, Stochastic depth, etc…

Regularization: Weight Decay

L2 regularization(=ridge regression)와 L1 regularization(=lasso regression)는 모든 가중치를 0으로 향하게 하여 큰 가중치를 제한합니다. 가중치가 양수면 감소하고, 음수면 증가시켜 결과적으로 모든 가중치가 0에 가까워집니다.

하지만 L2 regularization는 가중치의 크기가 커질수록 페널티가 가속적으로 증가하고, L1 regularization는 가중치의 크기에 비례하여 선형적으로 페널티를 부과한다는 특징이 있습니다.

  • L2 regularization (=ridge regression)
    wj=Wj+hyixijexp(−yi(w∗xi+b))=h∣wjw_j = W_j + hy_ix_{ij}exp(-y_i(w*x_i + b)) = h|w_j

  • L1 regularization (=lasso regression)
    wj=Wj+hyixijexp(−yi(w∗xi+b))=h∣sing(wj)w_j = W_j + hy_ix_{ij}exp(-y_i(w*x_i + b)) = h|sing(w_j)

Gradient descent

  1. 초기 가중치 값(Weights, W) 값을 아무 값이나 정해서 시작합니다.
  2. 현재 가중치로 loss가 얼마나 큰지 확인합니다. 목표는 loss를 최소화하는 것입니다.
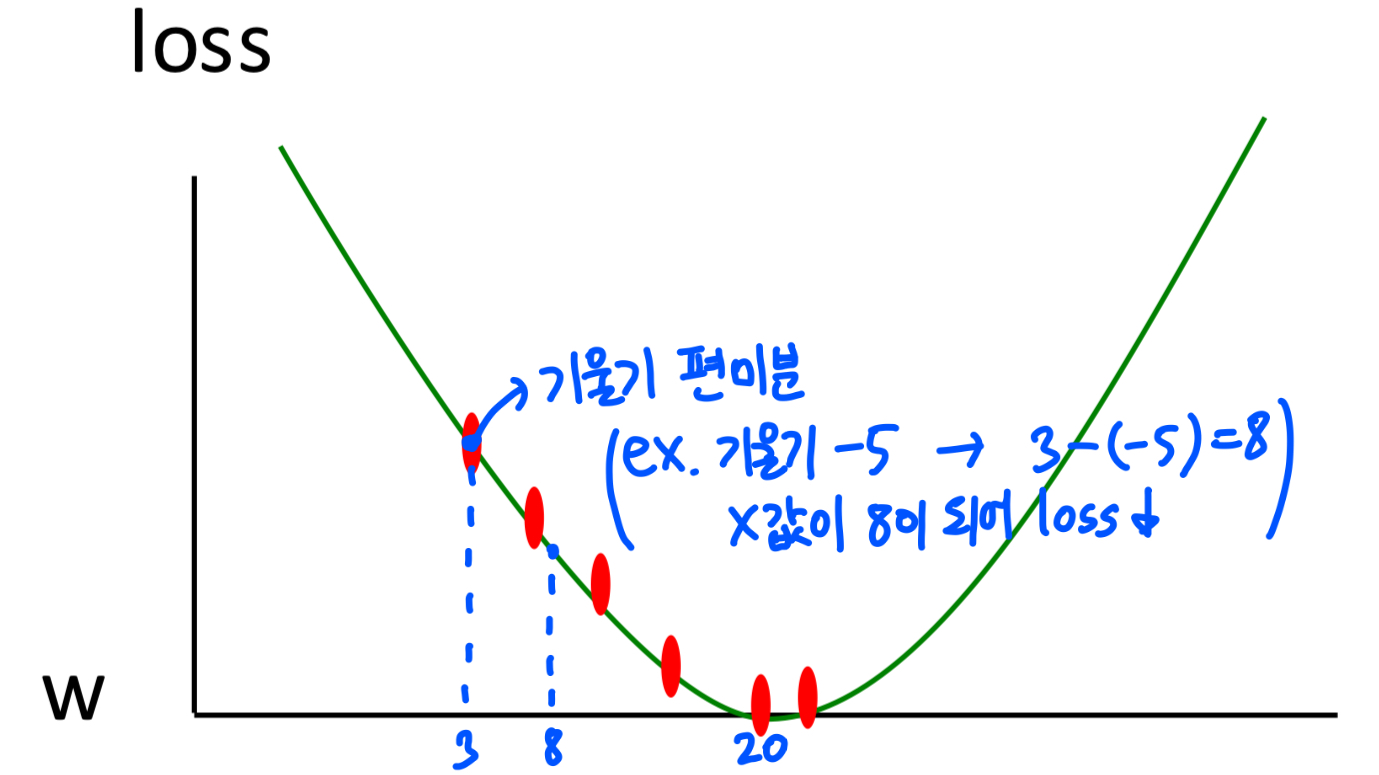
  3. loss function의 기울기(Gradient)를 계산(도함수 사용)합니다. 기울기는 함수의 현재 위치에서 어느 방향으로 움직이면 손실이 줄어들지를 알려줍니다. (기울기가 양수이면 왼쪽, 음수이면 오른쪽으로 이동)
  4. 계산된 기울기를 바탕으로 가중치를 소량 이동시킵니다. 위 과정을 모든 가중치 차원(Dimension)에 대해 반복하면서 손실이 점점 줄어드는 방향으로 이동합니다. 손실(Loss)이 0에 가깝거나 더 이상 줄어들지 않을 때 멈춥니다.

Regularization: Dropout

Dropout은 training 중에 랜덤으로 일부 뉴런과 연결을 제거하여 overfitting을 방지하는 방법입니다.

각 뉴런이 삭제(drop)될 확률 p는 다른 뉴런과 독립적으로 결정됩니다. 예를 들어, 한 뉴런이 80% 확률(p=0.8)로 유지된다면, 다른 뉴런의 상태에 상관없이 독립적으로 결정됩니다. 즉, 어떤 뉴런이 삭제될지, 남을지는 각 유닛마다 랜덤하게 결정됩니다.

또한 p는 뉴런이 유지될 확률을 나타내는 하이퍼파라미터입니다. 일반적으로 학습 중 뉴런의 20%에서 50% 정도를 삭제(즉, p=0.8 또는 p=0.5)하는 것이 효과적이라고 알려져 있습니다. p의 값은 실험적으로 설정되며, 모델의 복잡도와 데이터셋의 크기에 따라 적절한 값을 찾아야 합니다.

일종의 앙상블 running으로, 하나의 모델을 여러 랜덤 Dropout 모델로 나누어 약간 다른 아키텍처로 훈련할 수 있습니다. 즉, 다양한 랜덤 구조를 가진 네트워크를 동시에 학습하는 효과가 있습니다.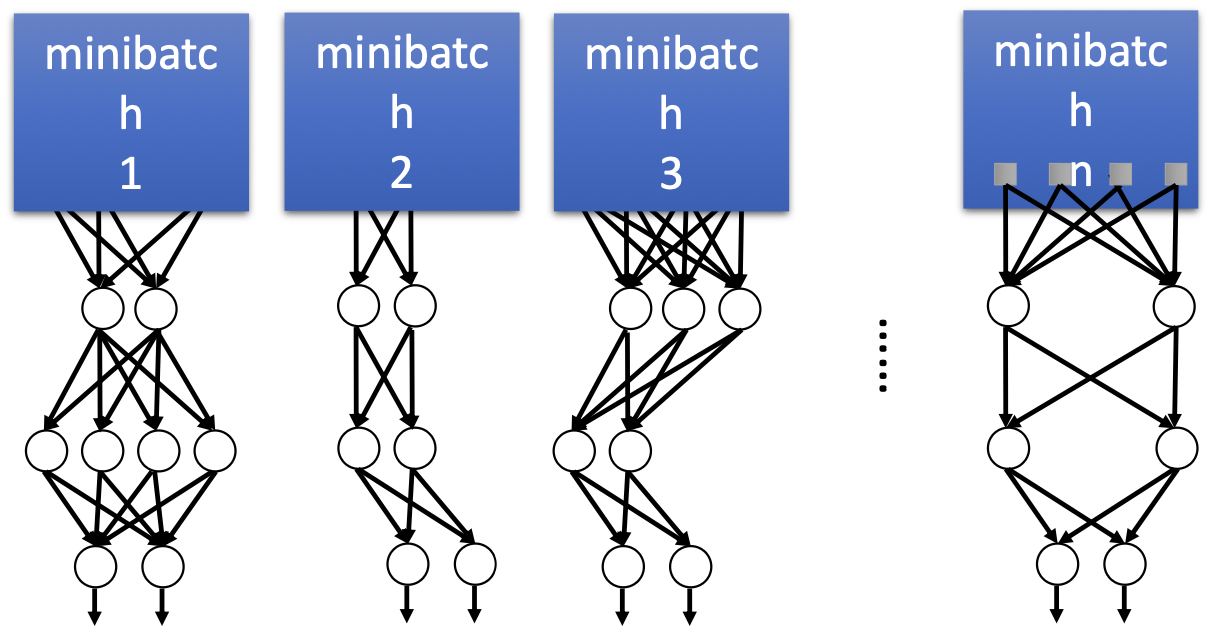

Regularization: Early Stopping

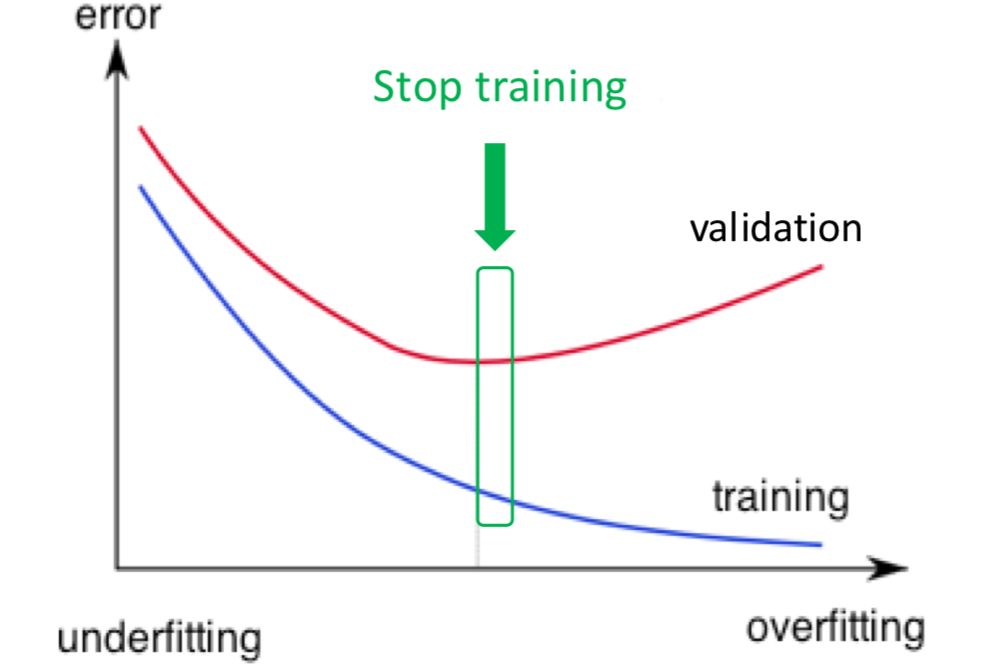
Early-stopping은 training 도중 validation set의 정확도가 더 이상 개선되지 않을 때 학습을 멈춰 overfitting을 방지하는 방법입니다.

model training 중에는 validation set를 사용합니다. (ex. 약 25%~75%의 validation/train 비율)

n개의 epochs 이후에도 validation 정확도(또는 loss)가 개선되지 않을 때 중지합니다. 매개 변수 n을 patience라고 합니다.

Activation Functions

deep neural network에 비선형 함수(ex. ReLU)를 사용하지 않는 경우 선형성이 유지되어 더 다양한 함수를 표현할 수 없게 됩니다. 그 이유로 인해 Activation Functions를 사용하는 것입니다.

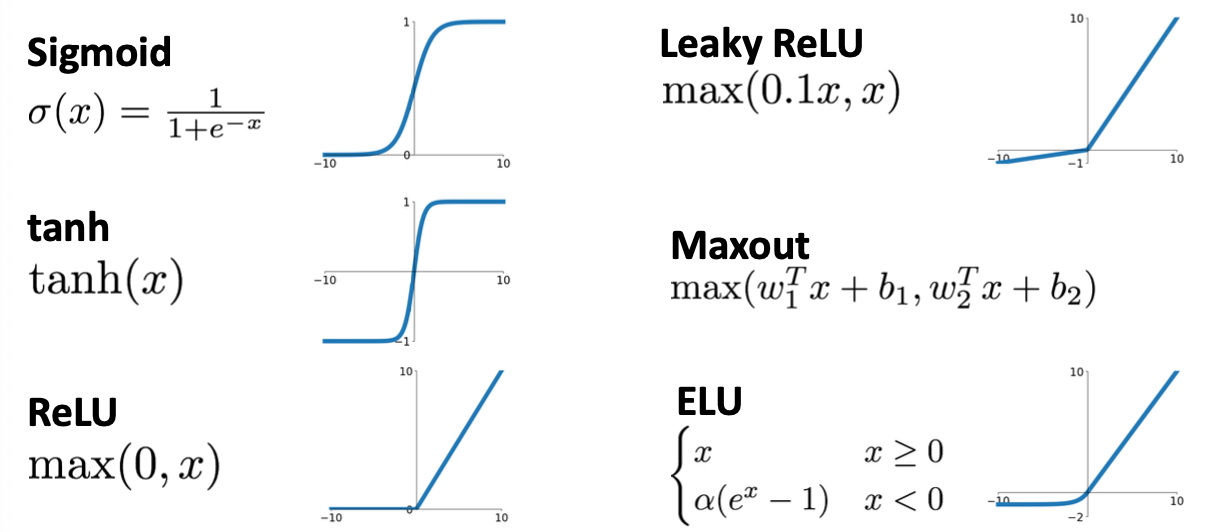
ReLU가 미분 계산이 편하기 때문에 ReLU를 가장 많이 활용합니다.

Biological Neuron

인간의 뉴런에서 나타나는 현상들을 수학적으로 나타낸 것이 현재의 Neural network입니다.

profile
해담
해담이를먹여살리기위한..
이전 포스트

Deep learning

다음 포스트

Backpropagation with Computational graph

0개의 댓글