[딥러닝] Decoupled Neural Interfaces using Synthetic Gradients (DNI)

Ethan·2023년 1월 18일

Papers Review

목록 보기

6/18

모든 Paper review는 제가 공부하고 남기는 기록입니다.
잘못된 내용이나 추가 의견이 있으시면 언제든 자유롭게 댓글 남겨주세요.

Published: Deepmind, 2016
Paper: https://arxiv.org/abs/1608.05343

2016년 딥마인드에서 나온 논문입니다.

당시엔 많이 주목을 받았다고 하는데, 어떤 이유로 지금은 그다지 언급되지 않고 있는지 이유를 생각하면서 논문을 읽어보도록 하겠습니다.

[요약]

기존의 신경망들은 가중치를 업데이트하기 위해 Forward-Backward 과정이 반드시 먼저 완료되어야 합니다. 이 때 Forward, Backward, Update Locking 문제들이 발생합니다.
Decoupled Neural Interfaces (DNI)는 Synthetic Gradient 개념을 도입하여 모듈(레이어, 뉴런)별로 병렬 학습이 가능한 weight update 방법입니다.
기존의 Backpropagation에서 가중치 업데이트 과정과 오차 전파를 위한 메모리 처리 과정을 분리한 것입니다.

[서론]

Abstract

Neural Network를 직접 훈련시키려면 일반적으로 계산 그래프를 활용하여 순전파와 역전파를 통해 가중치를 업데이트하는 과정을 거쳐야 합니다.
그래서 NN의 각 레이어, 정확히는 네트워크를 구성하는 각 모듈들은 순전파-역전파 과정을 거쳐 가중치가 업데이트될 때까지 기다려야 합니다. 이걸 Locking이라고 합니다. 본 논문에서 제시하는 Decoupled Network Interfaces (DNI)는 이러한 locking 문제를 해결하기 위한 방법입니다.
DNI는 backpropagation 과정에서 모델링한 synthetic gradient를 가지고 각 뉴런들을 비동기 방식으로 업데이트하는 방법입니다. local information만 가지고 modelled subgraph의 연산 결과를 추정하는 것이죠. 또한 이러한 gradient approximating 방식은 input 예측에도 사용할 수 있다고 합니다.

1. Introduction

Locking 문제에는 몇 가지 종류가 있습니다.

1) Forward Locking
모든 모듈은 이전 모듈의 순전파 작업이 끝나기 전까지 입력 데이터를 처리할 수 없습니다. $f_2$ 레이어의 입력은 $f_1$ 레이어의 출력을 받는 형태로 되어 있기 때문입니다.

2) Update Locking
모든 모듈은 연결된 모듈들의 순전파가 모두 끝나기 전까지 가중치를 업데이트할 수 없습니다. Backpropagation 알고리즘은 최종 출력을 Loss값으로 잡고 시작하기 때문입니다. (최종 계산 결과를 알기 전까지 각 뉴런들의 가중치를 얼마나 수정해야 하는지 알 수 없음)

3) Backward Locking
2번과 같은 이유로, Backpropagation을 포함해서 많은 credit-assignment 알고리즘은 연결된 모듈들의 순전파-역전파 과정이 모두 끝나기 전까지 가중치를 수정할 수 없습니다.

주1:
Credit-Assignment는 신뢰 할당이라고 번역되며, 보통 강화학습 분야에서 많이 사용하는 용어입니다. Credit-Assignment Problem은 "네트워크를 구성하는 모듈들의 기여도를 파악할 수 있는가?" 에 대한 문제입니다.

예를 들어 오차역전파 알고리즘은 오차 전파 과정에서 각 레이어의 weight가 얼마나 업데이트 되어야 하는지 알 수 있기 때문에 Credit-Assignment 알고리즘이라고 할 수 있습니다.

Locking 문제 때문에 DNN은 순차적/동기적(sequential, synchronous)으로 학습해야 한다는 제약이 생기게 됩니다. 만약 병렬적으로 가중치를 업데이트할 수 있다면 학습 속도가 크게 향상될 수 있겠죠?
본 논문에서 해결하고자 하는 문제는 Update Locking입니다. 구체적으로는 아래와 같이 backprop을 쓰지 않고 모듈 $i$ 의 가중치 $\theta_i$ 를 추정하는 방법을 제시했습니다.

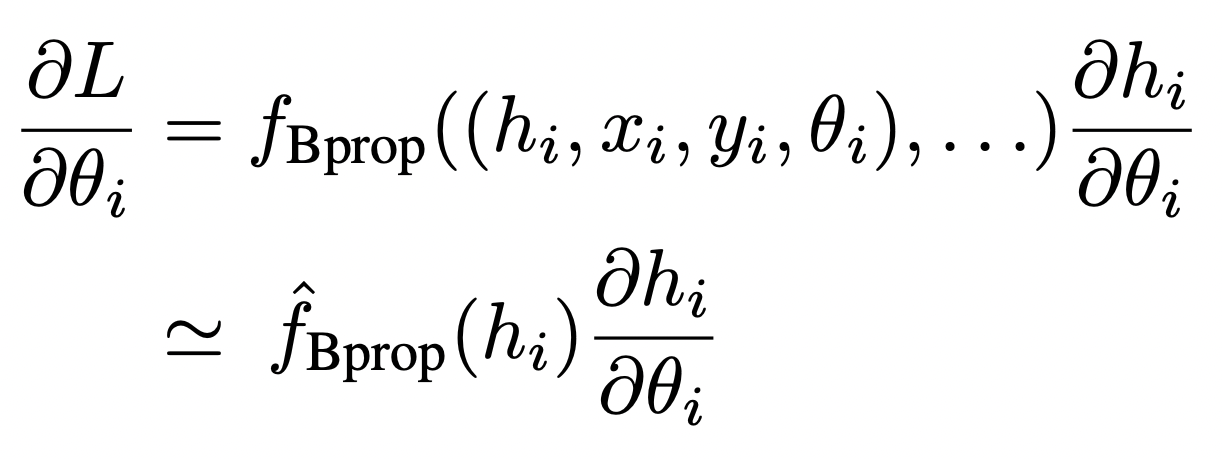
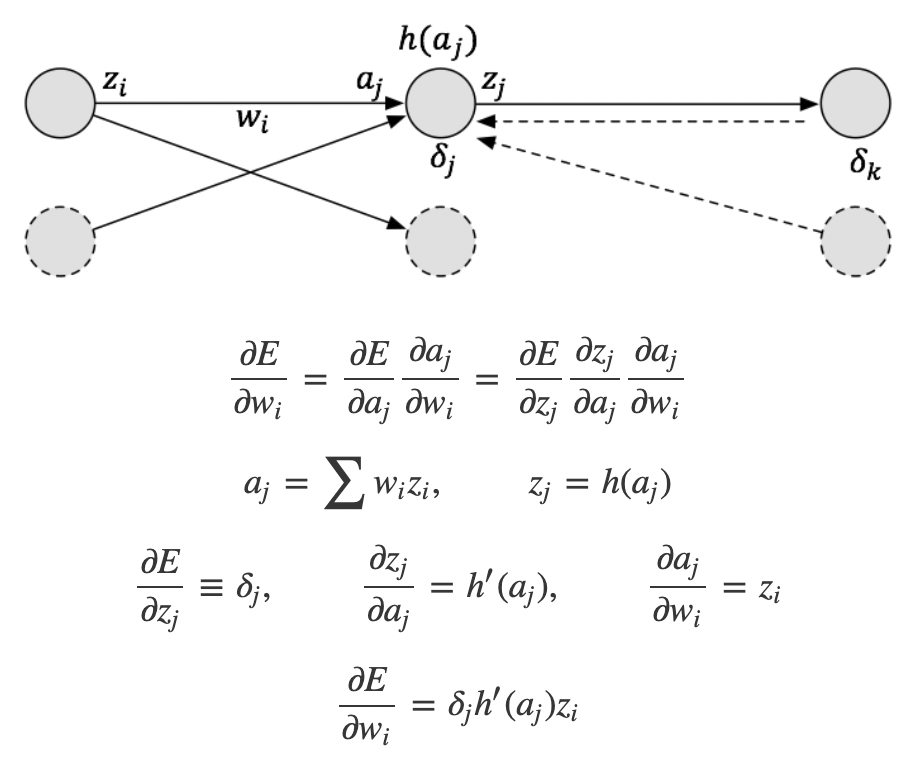
$h$ 는 모듈의 출력값인 activation, $x$ 는 입력값, $y$ 는 supervision (label 등), $L$ 은 최적화해야 하는 loss function입니다.

원래 수식은 $h_i, x_i, y_i, \theta_i, ...$ 이 필요한 반면,
해당 식을 근사한 $\hat f_{\mathrm{Bprop}}(h_i){\partial h_i\over \partial \theta_i}$ 에서는 $h_i$ 정보만 있으면 됩니다.

즉, 임의의 모듈 $f_n$ 은 $f_{n-1}$ 에서 보내준 activation 정보만으로 자신의 error gradient 값을 업데이트할 수 있게 되는 것입니다. 이렇게 계산한 gradient 값을 Synthetic Gradients 라고 합니다.

이와 같은 방식으로 Update locking을 제거하면 각 모듈이 병렬적으로 학습할 수 있습니다.

주2:
논문에는 중간 과정이 생략돼 있는데, norman3님 블로그에 자세하게 설명된 내용이 있어 참고하면서 이해해 보겠습니다.

레이어 $f_i \rightarrow f_j$ 일 때,

$z_i=f_i$ 의 출력,
$w_i=f_i$ 의 가중치,
$a_j=f_j$ 의 입력,
Synthetic gradient $\delta$ 라고 하면,

구하고자 하는 가중치 ${\partial L\over \partial w_i}={\partial L\over \partial a_j}{\partial a_j\over \partial w_i}={\partial L\over \partial z_j}{\partial z_j\over\partial a_j}{\partial a_j \over \partial w_i}$ 가 됩니다.

$a_j=\sum w_iz_i$ 이고, $z_j=h(a_j)$ 이므로

${\partial L \over \partial z_j}=\delta_j, \quad{\partial z_j\over\partial a_j}=h'(a_j), \quad{\partial a_j \over \partial w_i}=z_i$ 가 됩니다.

따라서 ${\partial L \over \partial w_i}= \delta_jh'(a_j)z_i$ 로 근사할 수 있습니다.
$\quad$

이에 따라 논문에서 표현한 $\hat f_{\mathrm{Bprop}}(h_i){\partial h_i\over \partial \theta_i}$ 식을 다시 바꿔보면,

${\partial h_i \over \partial \theta_i}=h'(a_j)$ 이고 $\hat f_{\mathrm{Bprop}}(h_i)=\delta_jz_i$ 가 됩니다.

[본론]

2. Decoupled Neural Interfaces

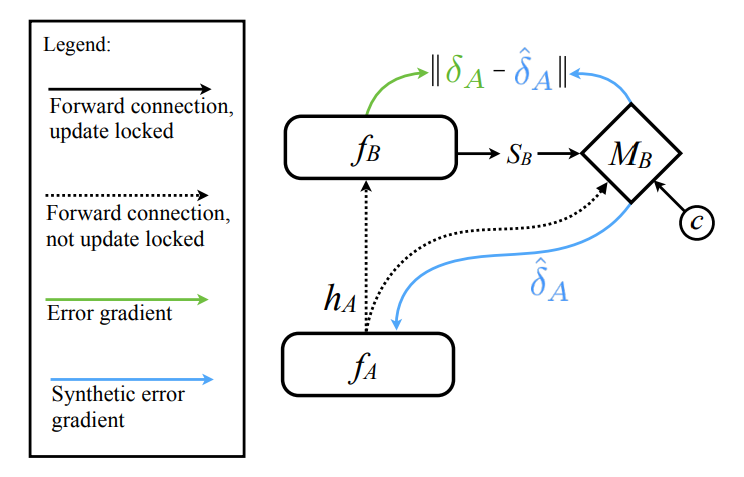
그림을 보면서 구체적인 작동 과정을 이해해 보겠습니다.

(1) 모듈 $f_A$ 는 activation $h_A$ 을 다음 모듈 $f_B$ 와 DNI 모듈 $M_B$ 에 전달합니다.

(2) $M_B$ 는 synthetic gradient $\hat \delta_A=M_B(h_A, s_B, c)$ 를 생성합니다.
$\quad$ ( $s_B$ = $f_B$ 의 일부 상태 정보, $c$ = 계산에 필요한 기타 정보)

(3) $f_A$ 는 $\hat \delta_A$ 를 전달받아 gradient 값을 업데이트합니다.

(4) $M_B$ 는 $f_B$ 에게서 진짜 그래디언트 값 $\delta_A$ 를 전달받아 오류를 수정합니다. $(\lVert \delta_A-\hat \delta_A\rVert )$

위 gif를 보면 메커니즘을 조금 더 쉽게 이해할 수 있습니다.

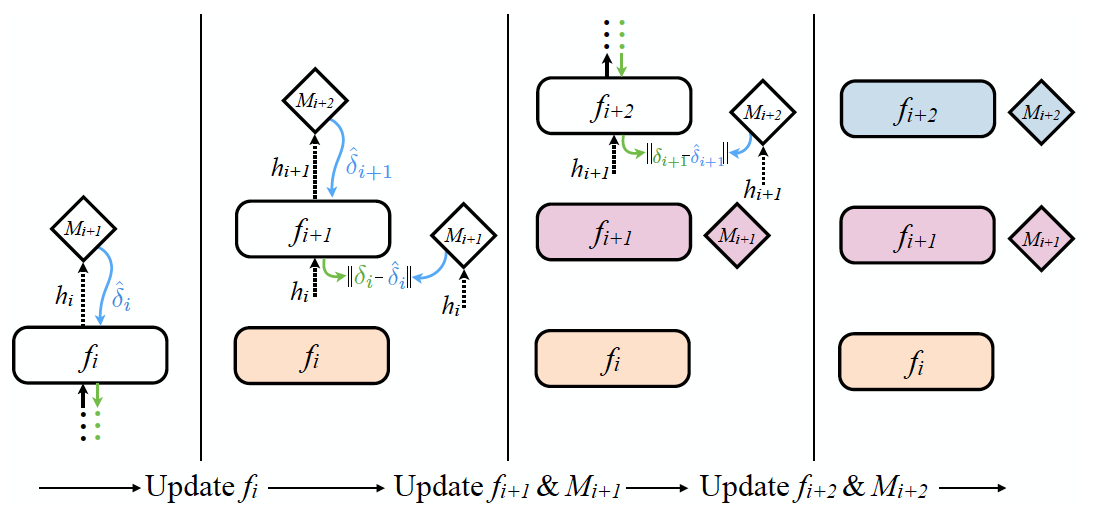
이번에는 여러 층을 가진 네트워크에 DNI를 적용하는 경우를 살펴보겠습니다.

(1) 먼저 $f_i$ 의 출력 $h_i$ 를 $M_{i+1}$ 에 전달합니다.

(2) $M_{i+1}$ 에서 $\hat \delta_i$ 를 전달받아 가중치를 수정합니다.

(3) 그 동안 $f_{i+1}$ 는 출력 $h_{i+1}$ 를 $M_{i+2}$ 에 전달합니다.

(4) $f_{i+1}$ 가 전달받은 $\hat \delta_{i+1}$ 을 $M_{i+1}$ 로 전달합니다.

(5) $M_{i+1}$ 의 가중치를 수정합니다. $(\lVert\hat \delta_i-\hat \delta_{i+1}\rVert)$

주3:

$M_{i+1}$ 업데이트에 사용되는 $\hat \delta_{i+1}$ 도 synthetic gradient이기 때문에, $\hat \delta$ 를 얼마나 잘 추정하느냐가 DNI 성능의 핵심이라고 볼 수 있습니다. 다만 DNI 모듈이 복잡해질수록 computational cost도 크게 증가한다는 단점이 있겠죠?

논문에서는 이러한 이유 때문에 단순한 MLP 네트워크를 통해 synthetic gradient를 추정합니다.

2.1 Synthetic Gradient for Recurrent Networks

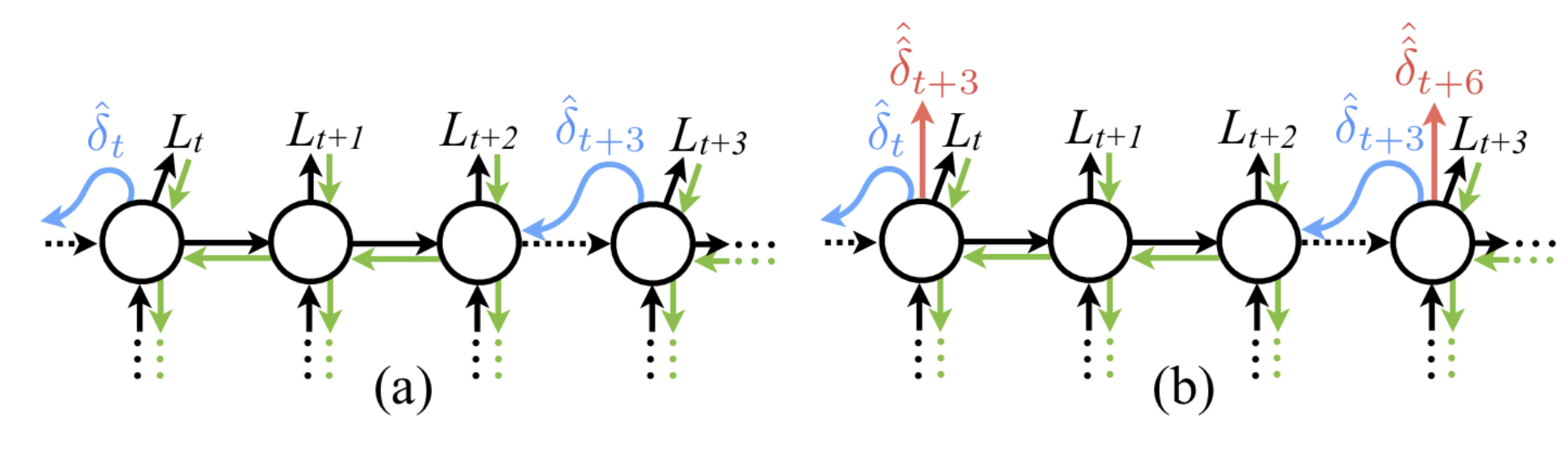
RNN과 같은 recurrent network에도 DNI를 적용할 수 있습니다.

(a)는 DNI를 적용한 truncated BPTT 방식으로 학습한 RNN입니다. 중요한 것은 (b) 그림처럼 future synthetic gradient를 예측할 수도 있다는 것입니다. 매 time step마다 synthetic gradient $\hat{\hat{\delta}}_{t+T}$ 를 생성하기 때문에 ( $T$ =truncate 단위), $\lVert \hat{\hat{\delta}}_{t+T}-\hat{\delta}_{t+T}\rVert$ 를 minize 해주는 방향으로 학습시키면 됩니다.

주4:

$\lVert \hat{\hat{\delta}}_{t+T}-\hat{\delta}_{t+T}\rVert$ 값을 최소화한다는 것은 truncated된 단위별로 최종 그래디언트 값을 예측할 수 있다는 것과 같습니다. 이게 무슨 말일까요?

위와 같이 무한하게 이어지는 RNN 구조가 있다고 가정해 보겠습니다. 이 모델에서 우리가 원하는 gradient 값은 다음과 같이 얻을 수 있습니다. ( $\alpha$ = learning rate)
$\theta \leftarrow \theta-\alpha \sum_{\tau=t}^\infty{\partial L_\tau \over \partial \theta}$
하지만 현실적으로는 time dependency 문제를 해결하기 위해 아래와 같이 Truncated BPTT 구조로 학습을 진행하게 됩니다.

식으로 표현하면 다음과 같습니다. (위 그림의 경우 T=3)
$\begin{aligned}\theta-\alpha\sum^\infty_{\tau=t}{\partial L_\tau\over \partial \theta}&=\theta-\alpha(\sum^{t+T}_{\tau=t}{\partial L_\tau \over \partial \theta}+(\sum^\infty_{\tau=T+1}{\partial L_\tau \over \partial h_T}){\partial h_T \over \partial \theta})&\\ \\&=\theta-\alpha(\sum^{t+T}_{\tau=t}{\partial L_\tau \over \partial \theta}+\delta_T{\partial h_T \over \partial \theta})\end{aligned}$
여기서 $\delta_T=0$ 으로 놓으면 식을 편하게 계산할 수 있습니다. 일반적으로는 이런 방법을 통해 gradient를 구하게 됩니다.

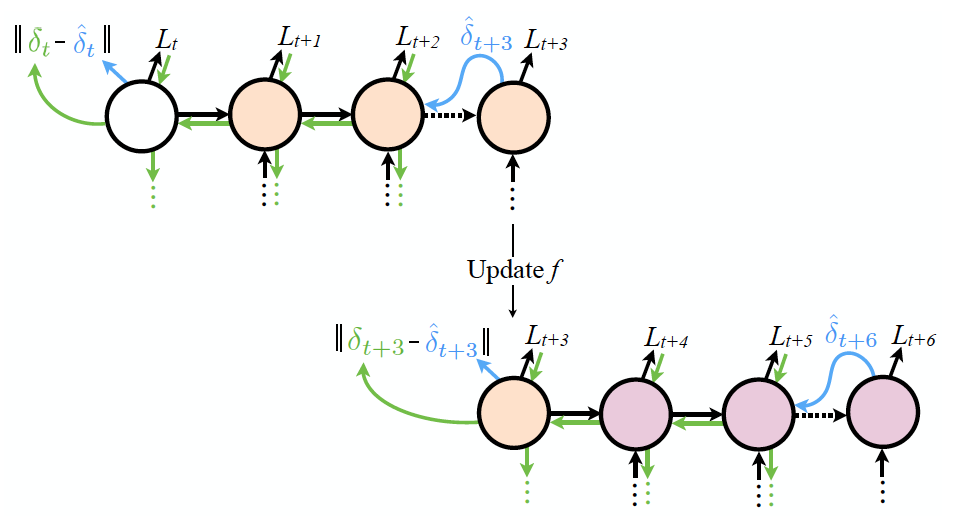
하지만 $\delta_T=0$ 이라는 가정은 상당히 naive합니다. n번째 truncated Loss 값을 추정하기 위해 n+1번째 truncated module까지는 최적화가 되었다고 보는 관점이니까요.

그래서 논문에서는 위와 같이 synthetic gradient를 써서 truncated 단위별로 업데이트하는 방식을 제안합니다. 그림을 보면 t+T 번째 노드에서 $\delta_{t+T}$ 값을 업데이트하고 있습니다. T개씩 노드를 묶어서 한 덩어리로 생각하는 것입니다. 아래 gif를 보면 더 이해가 잘 될 겁니다.

2.2 Synthetic Gradient for Feed-Forward Networks

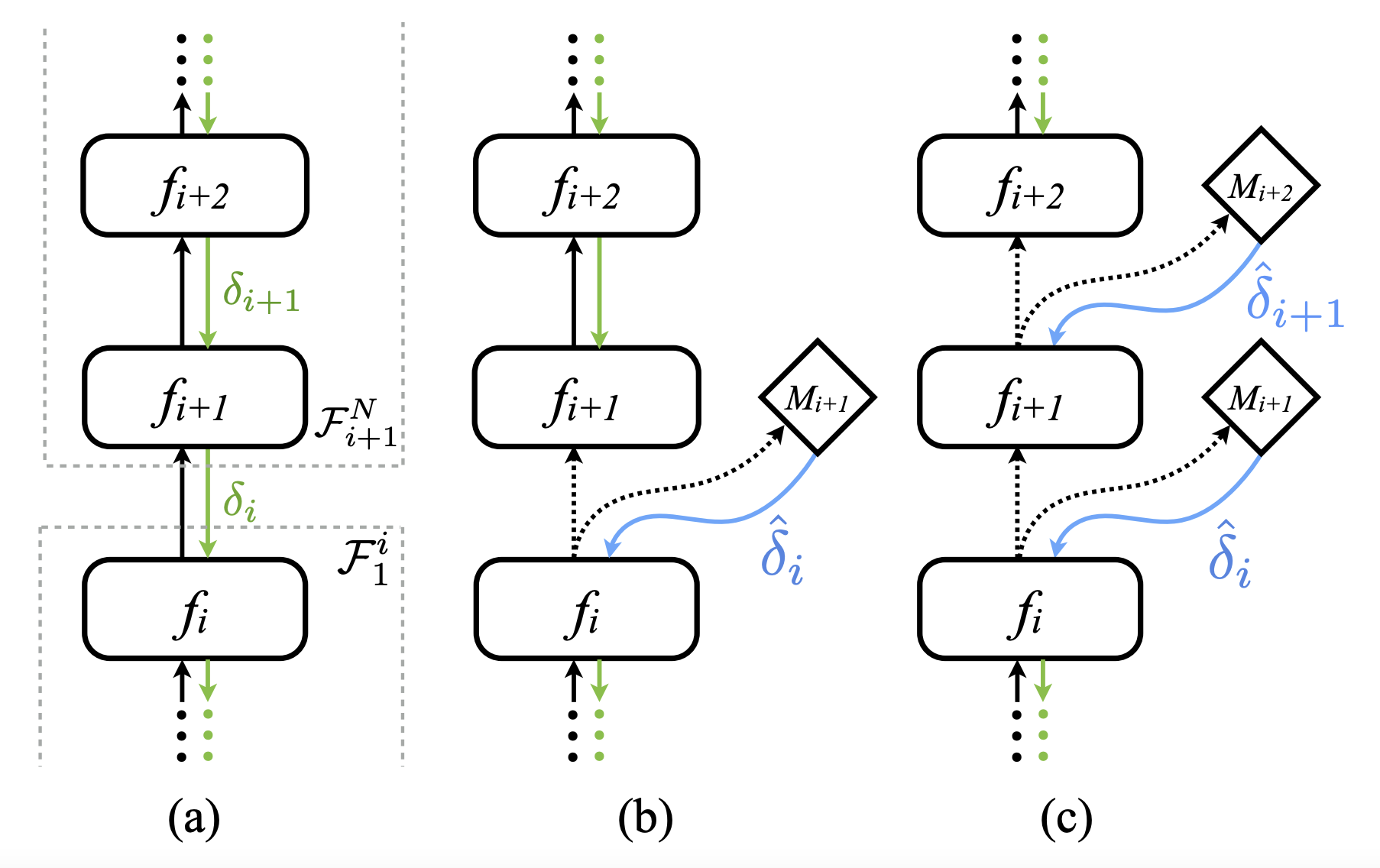
feed forward network에도 마찬가지 방식으로 DNI을 적용할 수 있습니다.

3. Experiments

상세한 실험 세팅은 논문을 참고하세요.

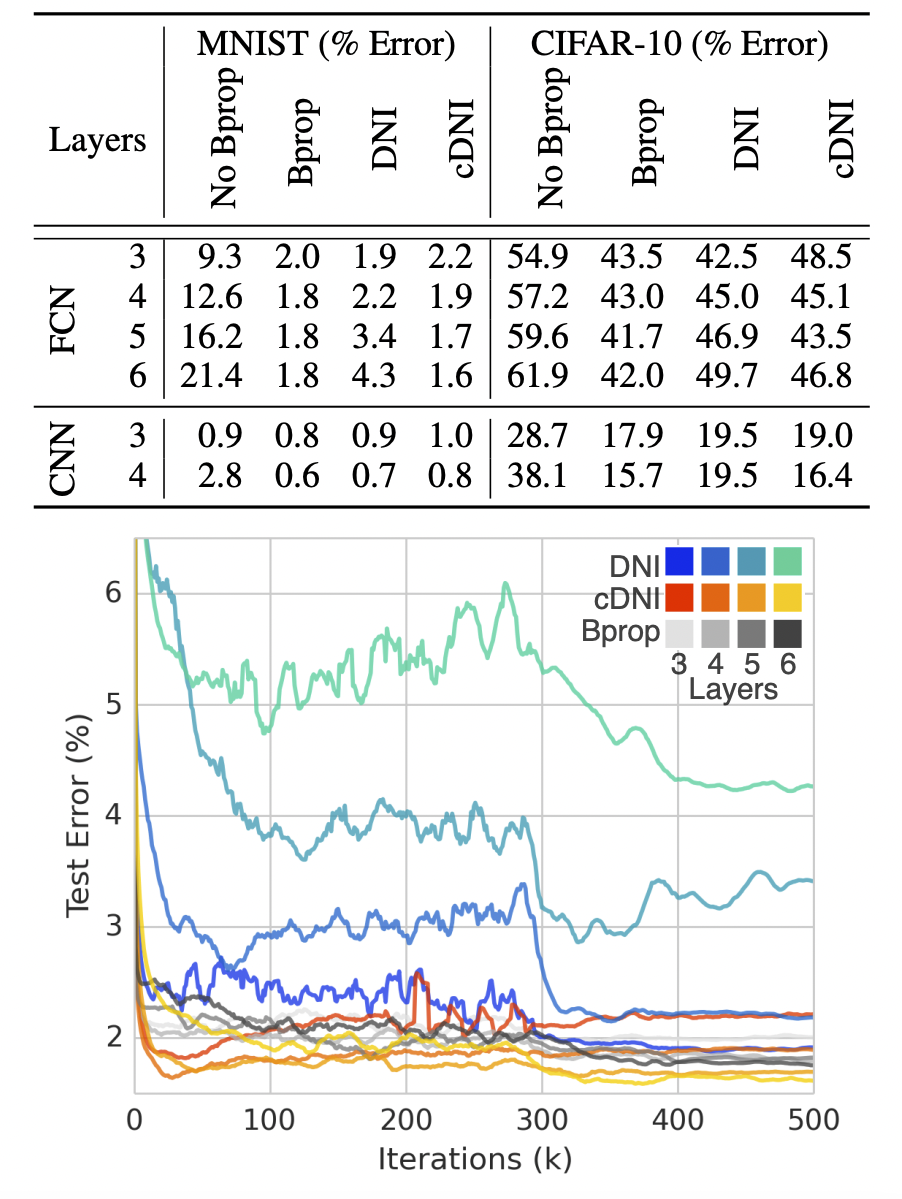
cDNI는 conditioned DNI로, 이미지의 label 값을 $c$ 에 추가한 버전입니다.
실험 결과를 보면 전반적으로 기존의 backprop보다 약간 더 높은 Loss를 보이지만 학습 결과는 거의 비슷합니다. 다만 그냥 DNI를 사용하기보다 cDNI를 사용하는 것이 훨씬 안정적인 학습이 가능합니다.

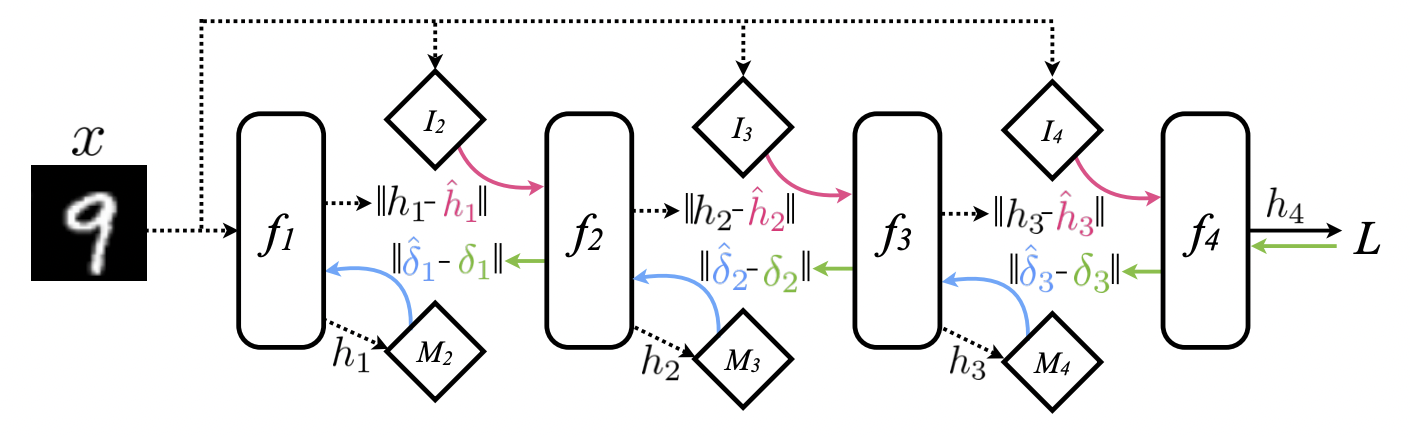
위와 같이 complete unlock 구조의 네트워크 학습도 가능합니다.
synthetic gradient 뿐 아니라 synthetic input도 사용합니다.

RNN 구조(LSTM)에서는 DNI를 적용하면 성능이 확연히 향상됩니다.

위 표에서 repeat copy는 복원에 성공한 시퀀스 수이고,
penn treebank는 BPC (Bits Per Character) 값입니다.

Aux는 Truncated 단위로 synthetic gradient를 업데이트하는 모듈입니다.

주5:

논문에는 RNN 구조에서 DNI 모듈이 성능을 향상시키는 원인에 대해 명확하게 설명하지 않습니다.

개인적인 생각으로는, Synthetic Gradient를 추정하는 과정에서 recurrent network 특유의 정보 소실 현상이 예방되는 효과가 나타난다는 가설 정도를 고려할 수 있을 것 같은데요.

실제로 위 실험 결과를 보면 Aux 모듈이 추가된 DNI의 성능이 더 뛰어납니다. 또한 표를 잘 보면 $T$ 값에 따라 성능 향상의 추이가 변화하는데, 이는 해당 모듈이 Truncated 단위 $T$ 기준으로 각 단위 모듈 간에 정보를 전달한다는 점을 고려했을 때, Approximated Residual 정도의 개념으로 이해할 수 있겠습니다.