
모든 Paper review는 제가 공부하고 남기는 기록입니다.
잘못된 내용이나 추가 의견이 있으시면 언제든 자유롭게 댓글 남겨주세요.Published: Journal of Machine Learning Research, 2014
Paper: https://jmlr.org/papers/v15/srivastava14a.html
굉장히 유명한 논문입니다. 드롭아웃 개념을 먼저 제시한 페이퍼가 있는데, 이 논문이 더 잘 정리되어 있어서 많이들 보는 것 같습니다. 메커니즘을 잘 몰라도 쓰는 데는 지장이 없지만, 기왕이면 잘 알아두면 좋겠지요.
[요약]
-
Dropout 기법을 제안
- 모델의 학습 과정에 확률적으로 노이즈를 추가하여 robustness를 강화하는 방법 -
확률적으로 생성되는 여러 개의 모델을 앙상블하는 것과 비슷함
[서론]
Abstract
Dropout(드롭아웃)은 overfitting을 해결하기 위한 테크닉입니다. dropout의 핵심 아이디어는 학습 도중에 랜덤하게 unit과 그 연결을 제거하는 것입니다. 이렇게 하면 각 유닛(노드, 뉴런)끼리 서로 과도하게 의존하는 현상을 방지할 수 있습니다.
Introduction
overfitting은 기본적으로 모델이 test data를 볼 수 없기 때문에 발생합니다. 학습에 사용한 sampled dataset이 noise, 또는 regularization으로 작용하는 상황인 거죠.
이 문제의 가장 이상적인 해결책은 가능한 모든 weight로 prediction을 진행한 후 평균을 내는 것입니다. 쉽게 말해서 발생 가능한 모든 데이터를 고려한다는 뜻입니다. 당연히 엄청난 cost를 요구하죠.
또 다른 방법은 여러 모델을 사용하는 model combination입니다. 이를 위해서는 각 모델의 구조가 다르거나, 모델별로 다른 데이터를 학습해야 합니다. 현실적으로 이 방법도 너무 높은 cost가 필요합니다.
드롭아웃은 이러한 문제를 해결할 수 있습니다.
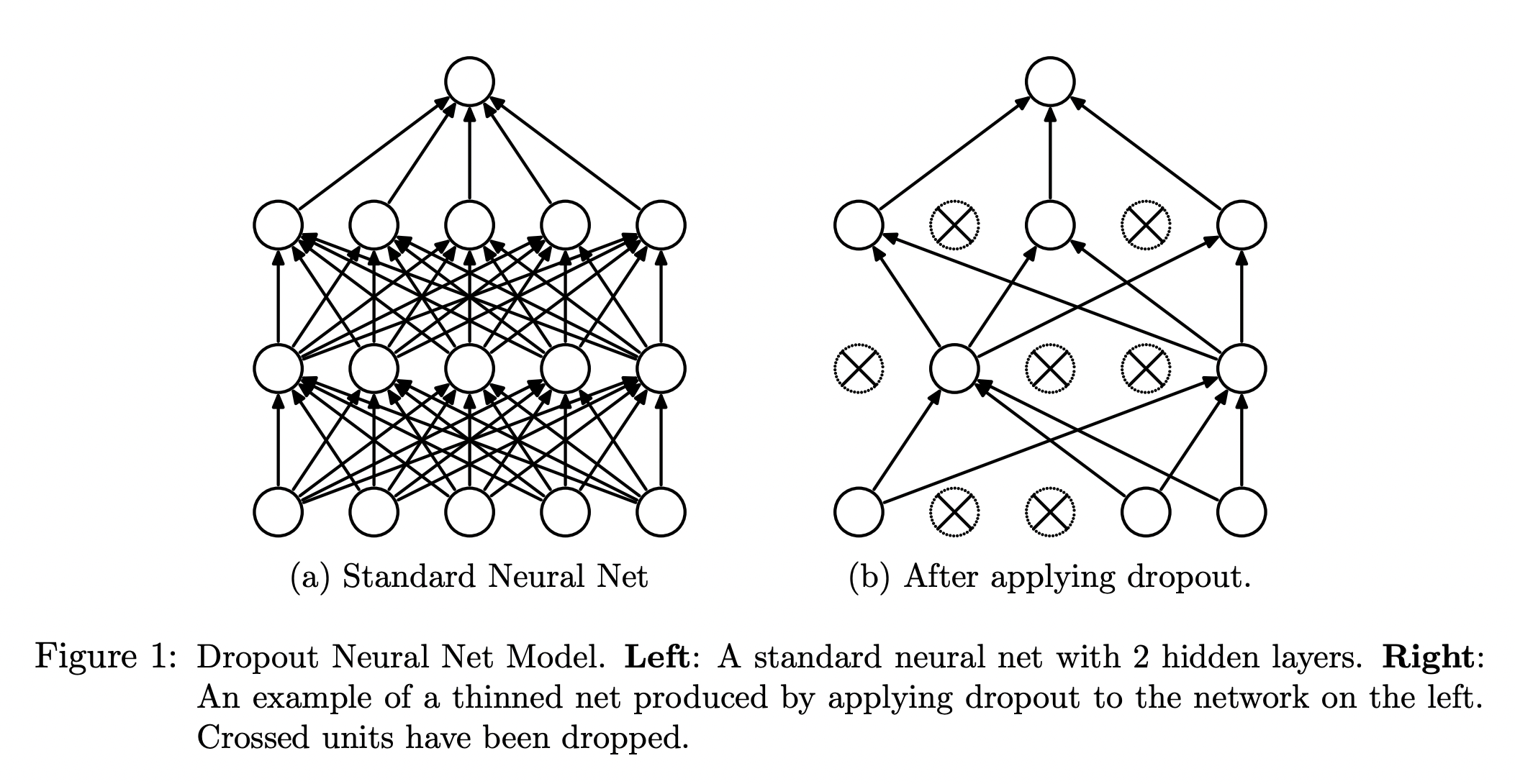
왼쪽은 하나의 단일 모델입니다. 하지만 오른쪽은 매번 확률적으로 다른 노드로 구성되기 때문에 여러 thinned model이 만들어지는 효과가 있습니다. 만약 개의 노드가 존재한다면, 가능한 전체 thinned model의 수는 각 노드를 쓸 지 말 지에 따라 개가 되겠지요.
각각의 thinned model은 가중치를 공유합니다. 매 번 다른 조합의 노드들이 활성화되더라도, 전체 네트워크를 구성하는 노드의 값이 많이 변하지는 않는다는 뜻입니다. 그래서 확률적으로 노드를 제거하여 매 학습마다 새로운 모델이 생성되더라도 실질적으로 새로운 학습은 거의 일어나지 않습니다. 즉, dropout을 적용하여도 가중치 자체는 크게 변하지 않습니다.
가중치가 거의 유지된다는 것은 모델의 일관성이 유지된다는 것과 같습니다.
직관적으로 이해해 보겠습니다. 오른쪽 눈으로 볼 때는 코끼리인 동물이 왼쪽 눈으로 봤더니 원숭이라면 과연 지금 보고 있는 것이 진짜 코끼리/원숭이인지 믿을 수 있을까요? 어느 쪽 눈으로 보느냐에 따라 약간의 위치 차이는 생길 수 있어도, 둘 다 동일하게 코끼리로 보여야 내가 보고 있는 것이 코끼리라는 확신을 가질 수 있을 겁니다.
학습마다 새로운 모델이 생성되는 것은 매번 다른 눈으로 보는 것과 같은 셈입니다.
자, 이제 이제 학습마다 생성된 수많은 thinned model들의 예측을 합치는 일만 남았습니다. 그런데 이들을 직접 평균내는 것은 매우 어려운 일입니다. 매번 Prediction을 가져다 평균을 내는 작업은 그냥 서로 다른 모델을 합치는 것과 다르지 않죠. 그래서 논문에서는 드롭아웃을 사용하지 않은 간단한 fully connect model을 가져다 approximating 하는 예시를 보여줍니다.
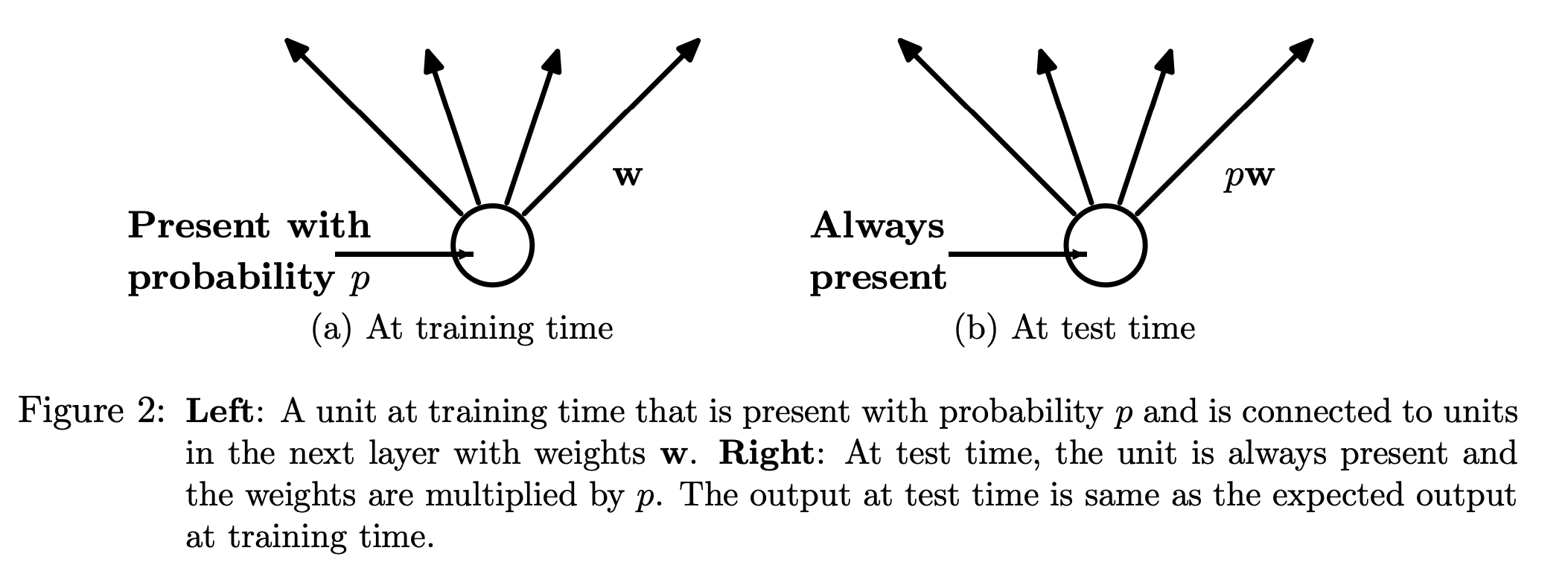
각 뉴런은 확률 에 따라 전달될 수도, 전달되지 않을 수도 있습니다. 하지만 test 시에 사용하는 approximating model은 모든 뉴런을 사용합니다. 따라서 각 뉴런에 확률 를 곱해서 기댓값을 얻는 방식으로 여러 개의 thinned model을 하나로 합친 가상의 final model을 추정할 수 있습니다.

나루토에서 분신들이 본체로 돌아가면 경험치가 늘어나는 것과 같은 원리라고 생각하면 됩니다.
Motivation
Dropout의 모티브는 유전학과 음모론이라고 합니다. 무성 생식보다 유성 생식이 더 진화된 전략인 이유는 유전자 풀의 다양성 확보 때문이고, 50명이 필요한 대형 음모를 한 번 시도하는 것보다 5명이 필요한 음모를 10번 시도하는 것이 더 큰 파급효과를 불러온다는 점에서 착안했다고 하네요. (오...)
Related Works
드롭아웃은 네트워크를 구성하는 hidden units에 노이즈를 더해줌으로써 regularization하는 방법의 일종으로 볼 수 있습니다. 노이즈를 더해준다는 점에서 Denoising AutoEncoder (DAE)와 비슷하죠. 차이가 있다면 DAE는 노이즈를 포함한 입력이 주어졌을 때 노이즈가 제거된 출력을 생성하지만, 드롭아웃은 전체 네트워크를 평균내는 방법으로 각 레이어에 고루 노이즈를 더해주는 효과를 냅니다.
논문에 따르면 드롭아웃은 주로 20% 또는 50%의 노드를 제거했을 때 가장 좋은 성능을 발휘했다고 합니다. (흔히 drop ratio를 heuristic하게 0.2 또는 0.5로 잡는데 이런 배경이 있었네요.)
[본론]
Model Description
개의 레이어를 가진 NN이 있다고 가정해 보겠습니다.
-
각 레이어
-
의 입력 / 출력 vector
-
= 의 가중치 / 편향
그러면 개의 레이어와 임의의 뉴런 에 대한 standard feed forward는 다음과 같이 나타낼 수 있습니다.
드롭아웃을 적용하면 다음과 같이 표현할 수 있습니다. (= element-wise product)
-
-
-
-
)
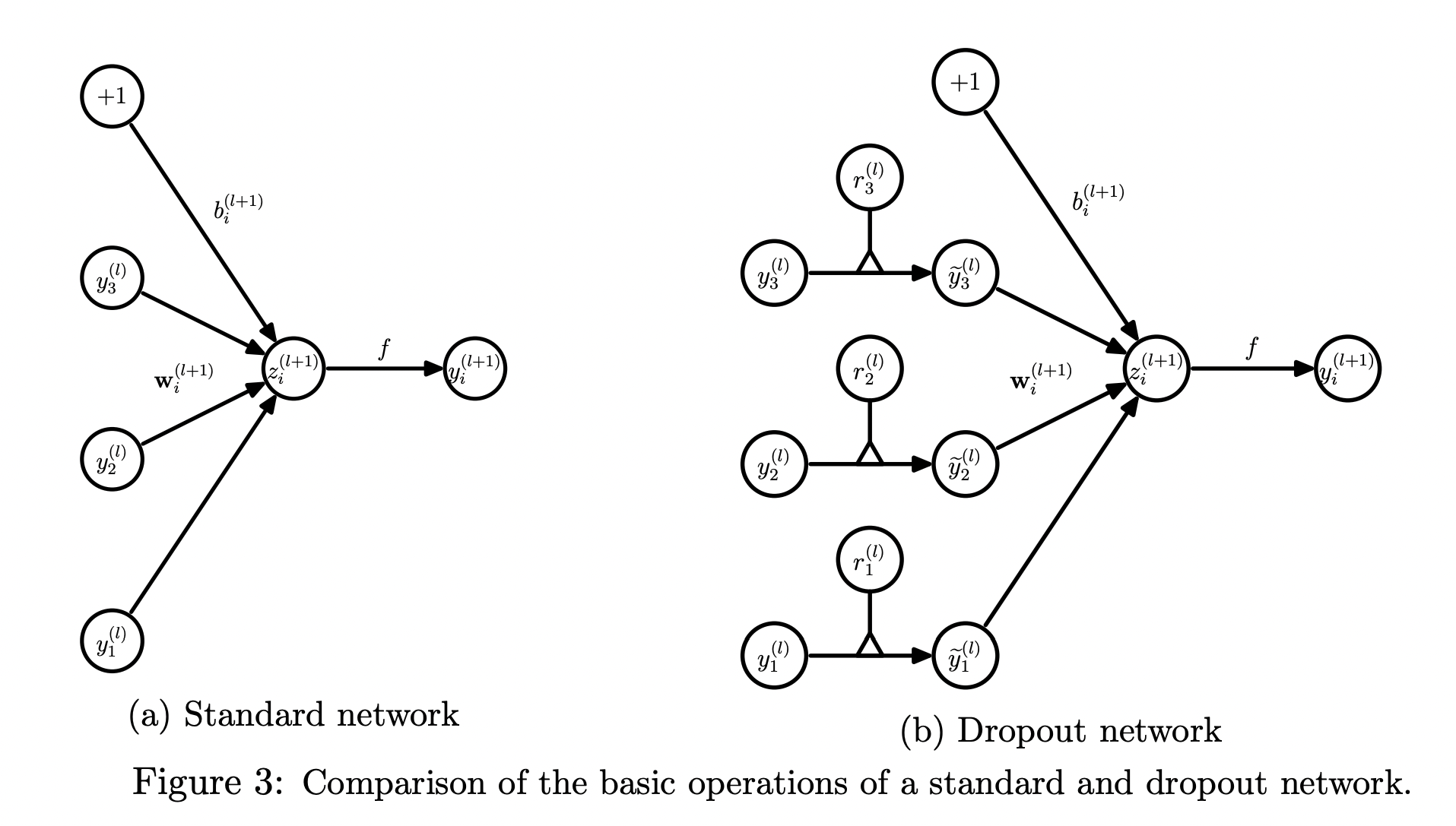
위와 같이 각 뉴런의 출력 에 확률변수 을 곱해주면 로 변환됩니다. 말 그대로 확률적으로 해당 뉴런을 쓸 지 말 지 결정하는 것입니다.
Learning Dropout Nets
Backpropagation
일반적인 NN처럼 SGD로 학습할 수 있습니다. 매 mini batch마다 드롭아웃을 실행하며, 해당 thinned network 단위로 forward/backward가 진행됩니다. 각 파라미터의 가중치는 각각의 미니배치에서 학습한 weights를 평균내서 구하게 됩니다. 또한 각각의 미니배치 학습 시 사용되지 않은 뉴런은 해당 파라미터의 가중치를 구하는 데 관여하지 않습니다. annealing, L2 weight decay, momentum같은 기법들도 잘 작동한다고 합니다.
특별히 드롭아웃과 잘 맞는 regularization 기법이 하나 있습니다. 바로 입력받는 가중치 벡터 의 norm값이 상수 보다 작도록 하는 것입니다. 의 값은 validation 과정을 통해 조절할 수 있습니다.
논문에서는 왜 두 방법이 궁합이 좋은가에 대해 다음과 같은 가설을 제시합니다.
먼저 Max-norm regularization을 사용하면 큰 learning rate를 사용해도 학습 과정이 불안정해지지 않습니다. 또한 드롭아웃에 의해 추가되는 noise는 원래대로라면 도달하지 못했을 다양한 region을 탐색할 수 있도록 합니다. max norm을 통해 드롭아웃의 단점을 예방해주는 셈이죠.
Unsupervised Pretraining
드롭아웃은 fine tuning에도 사용할 수 있습니다. pretrained weight에 를 곱해주면 됩니다. 이렇게 하면 학습 과정에서 드롭아웃을 적용한 것과 동일한 기댓값을 얻을 수 있습니다.
드롭아웃 기법의 확률적 특성 때문에 pretrained weight가 변형되는 것을 막기 위해 가중치를 임의로 초기화했을 때보다 더 작은 learning rate를 사용해야 한다고 합니다.
우리가 pretrained model에 기대하는 것은 weight surface 상에서 더 빨리, 그리고 넓은 optimal solution을 찾도록 도와주는 것입니다. fine tuning을 시작하는 시점에서는 당연히 그만큼 optimal solution region 근처에 있을 확률이 높으므로, 아예 처음부터 optimum을 찾아갈 때보다 작은 learning rate를 사용해서 세밀한 탐색을 하는 것이 적합하다고 볼 수 있습니다.
Experimental Results
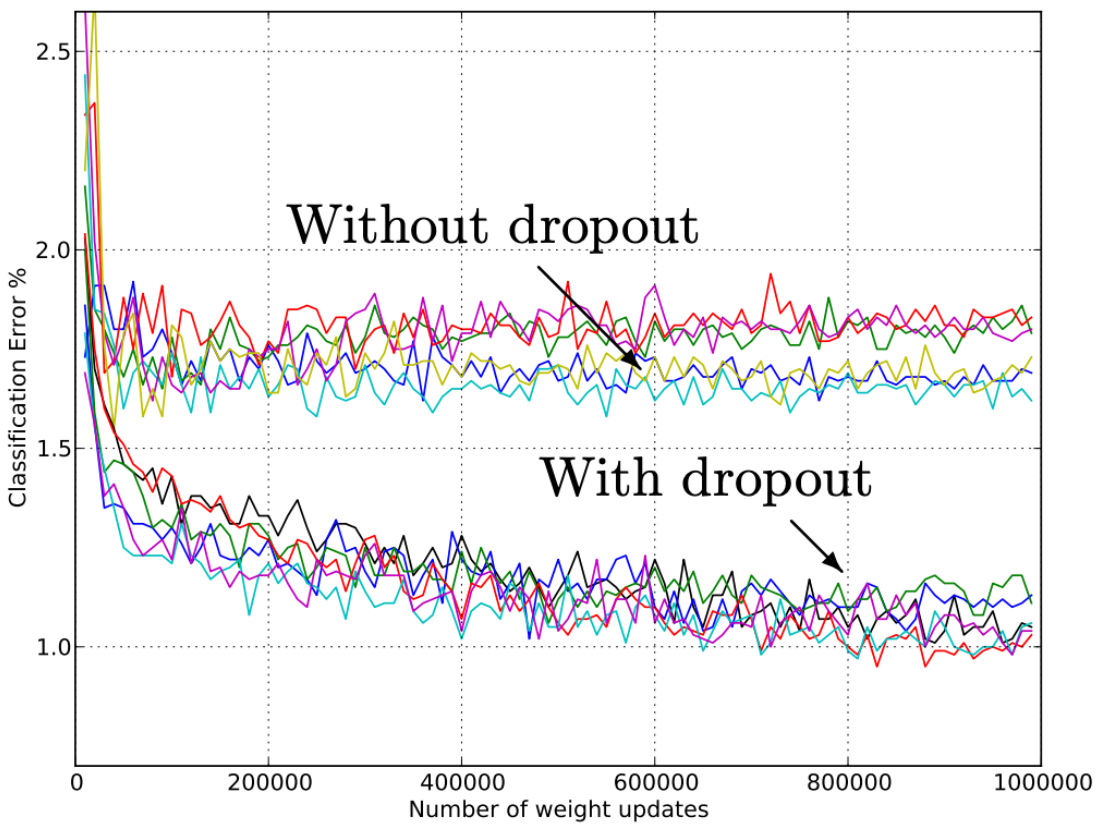
실험 결과는 위와 같습니다. 상세한 실험 내용과 과정이 궁금하면 논문을 참고하세요.
Salient Features
Effect on Features
논문에서는 overfitting이 일어나는 과정을 다음과 같이 설명합니다. DNN에서 각 파라미터(=feature)는 다른 뉴런들이 어떤 상태인지에 대한 정보를 전달받아(역전파 등) loss값을 감소시키는 방향으로 업데이트됩니다. 결과적으로 각 파라미터는 다른 파라미터를 보정하는 방식으로 작동하게 될 것입니다.
문제는 이런 방식의 학습은 파라미터 또는 뉴런 간의 상호의존성을 불러일으키기 쉽다는 것입니다. 그 결과 unseen data에 대한 general 성능이 감소합니다.

드롭아웃은 각 뉴런/파라미터 간의 연결을 랜덤하게 끊어줌으로써 이러한 상호의존성을 감소시킵니다. 위 두 그림은 서로 비슷한 수준의 test error를 가지고 있지만, 한눈에 봐도 왼쪽이 훨씬 dense합니다. 뉴런끼리의 density가 감소하면 더 적은 정보를 가지고 판단해야 하므로 상대적으로 중요한 feature가 추출되는 효과가 있습니다.
Effect on Sparsity
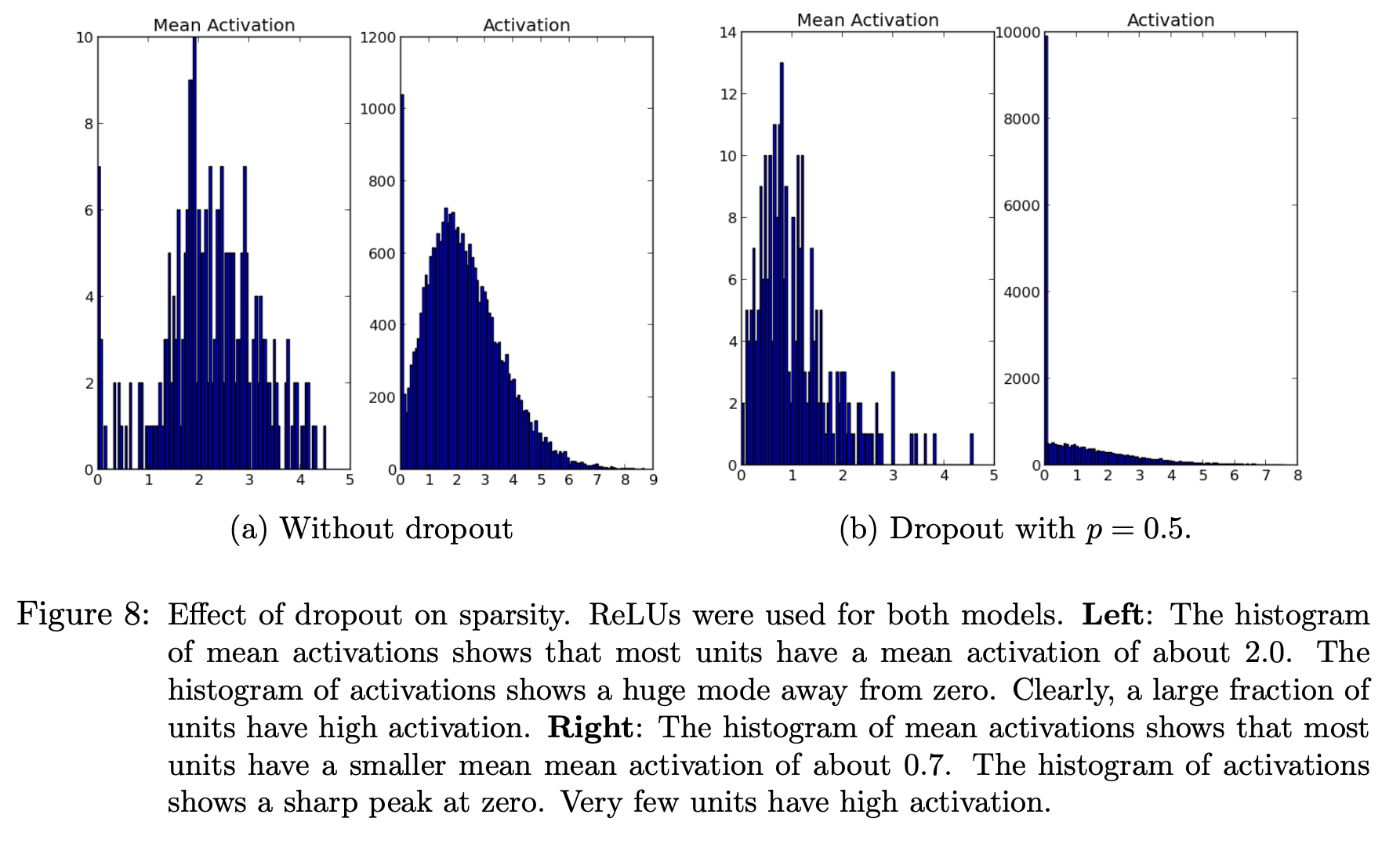
드롭아웃은 hidden unit의 activation을 sparse하게 만들어주는 효과도 있습니다. 위 그림을 보면 드롭아웃을 적용했을 때 hidden unit들이 less active해지는 것을 볼 수 있습니다. 두 모델의 test error가 비슷한 수준임을 고려하면, 뉴런을 덜 사용하고도 더 좋은 성능을 뽑아낼 수 있다는 것을 의미합니다.
activation이 sparse하다는 것은 activation function의 출력값이 0인 뉴런이 많다는 의미입니다.
Effect of Dropout Rate
최적의 값을 찾기 위해 아래의 2가지 조건으로 각각 실험을 진행했습니다.
1) hidden unit 수를 고정
2) 드롭아웃 후의 hidden unit 수가 같도록 에 따라 hidden unit 수를 조정
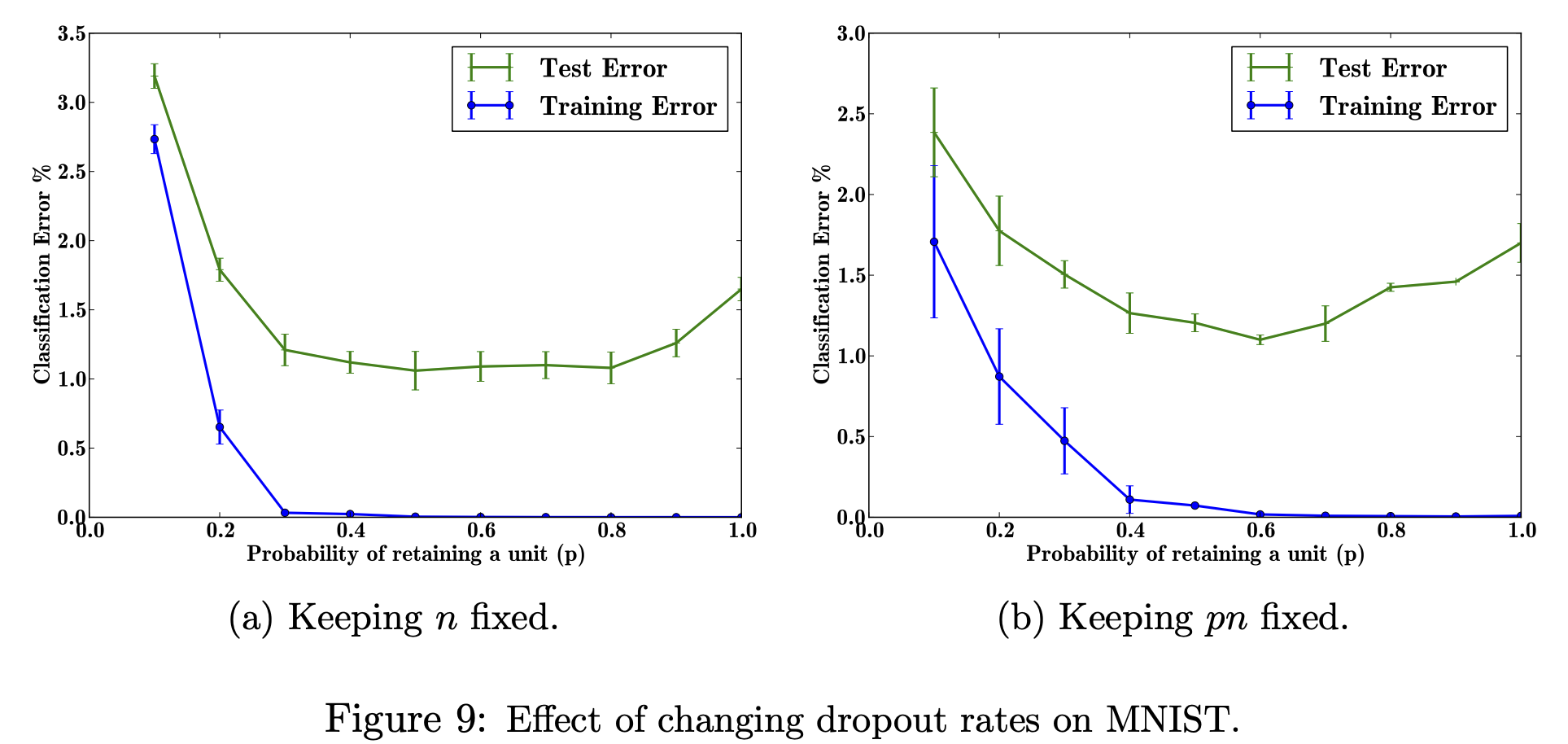
실험 결과는 위와 같습니다. 어느 조건이든 까지는 error가 계속 감소했지만, 부터는 error가 거의 감소하지 않거나 오히려 증가했습니다.
Effect of Data Set Size
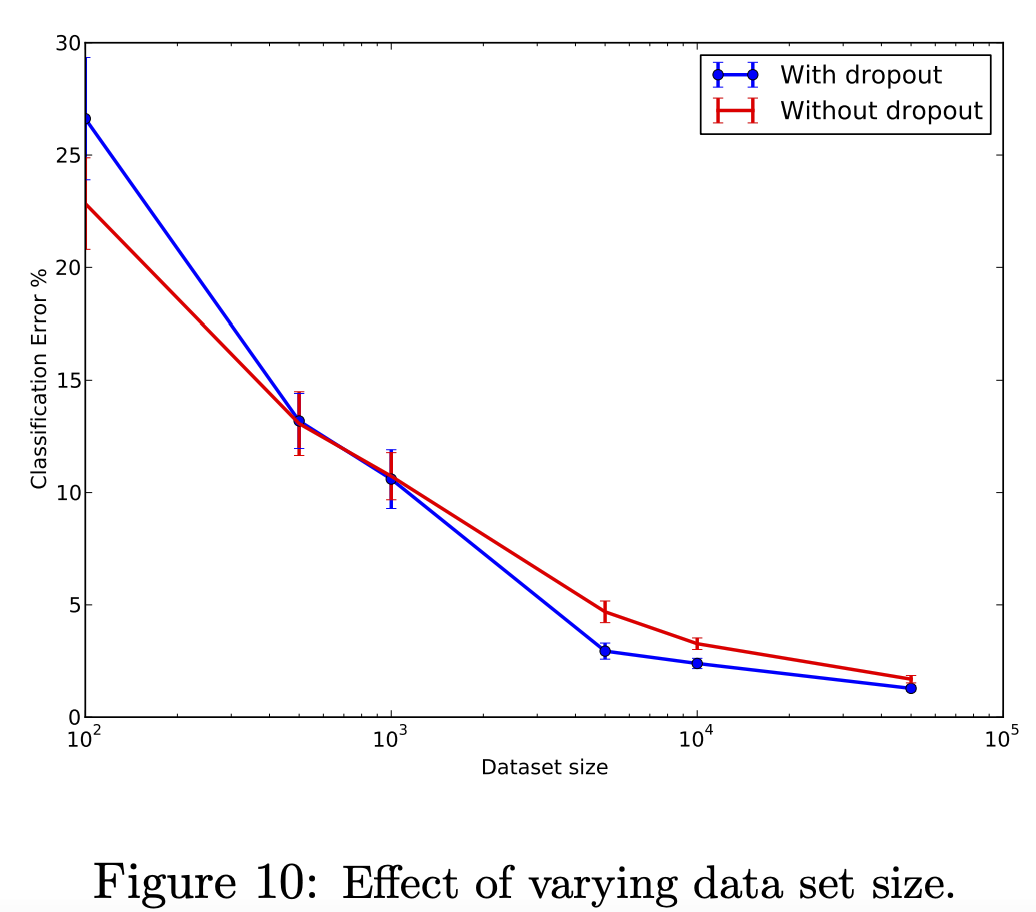
데이터셋 크기에 따라서도 dropout의 효율이 변합니다. 구체적으로는 크기는 넘어야 드롭아웃의 효과가 나타납니다. 물론 그렇다고 데이터가 커질수록 효과가 드라마틱하게 커지지도 않는데, 논문에서는 애초에 데이터가 클 수록 overfitting 가능성이 낮아지기 때문이라고 설명합니다.
Monte-Carlo Model Averaging vs. Weight Scaling
원래 논문에서 제안한 방법은 효율성을 위해 학습한 네트워크의 weight를 downscaling하여 model combination을 근사하는 것이었습니다. (전체 뉴런에 확률 를 곱해서 학습 과정에서 생성되는 을 근사)
만약 비용적 측면을 고려하지 않을 경우, 더 정확한 방법은 개의 샘플을 뽑아서 test시에도 드롭아웃을 적용한 후 그 결과들을 평균내는 것입니다. 몬테카를로 방법이죠.
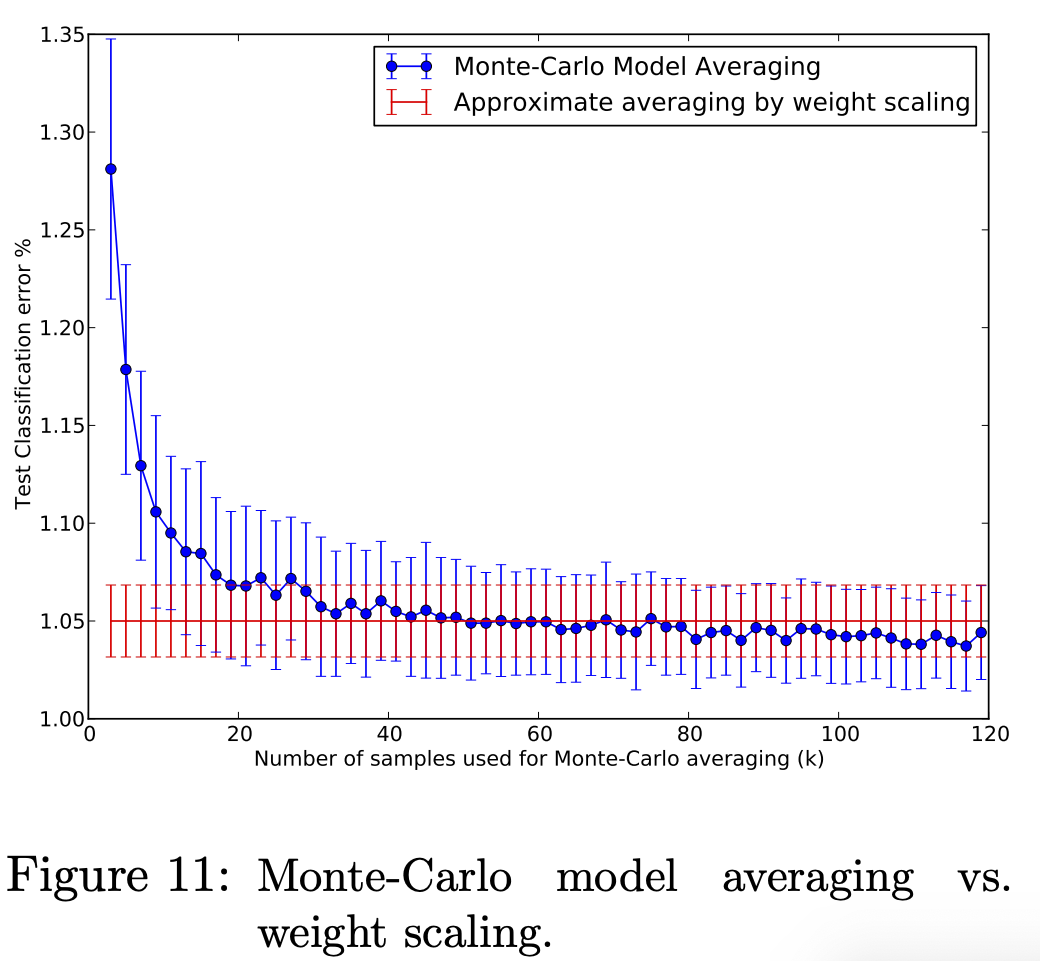
위 그림을 보면 몬테카를로 방법을 쓰는 것과 논문에서 제안한 approximate 방법을 사용하는 것의 차이를 알 수 있습니다. 값이 커질 수록 서로 비슷하게 수렴하게 되며, 평균적으로 이후부터 거의 같은 결과를 얻을 수 있다고 합니다.
Marginalizing Dropout
Linear Regression을 이용해서 드롭아웃의 stochastic한 특성을 deterministic하게 바꿀 수 있습니다. 상세한 과정은 논문을 참고하세요.

덕분에 드롭아웃 잘 이해하고 가요. 감사합니다
블로그 마다 예측시에 스케일링 vs 모델 평균으로 나뉘어져 있어서 혼동이 있었는데 잘 정리해주셔서 감사합니다
그런데 p와 1/p을 확률변수라 칭하는것은 적절하지 않아 보이네요
초매개변수 p가 적당할 것 같습니다