1. 모델 성능 평가

• 분류모델 평가

  • 분류 모델은 0인지 1인지 예측하는 것
  • 예측 값과 실제 값이 비슷할 수록 좋은 모델임
  • 정확히 예측한 비율로 모델 성능 평가

• 회귀모델 평가

  • 회귀 모델은 정확한 값을 예측하기 어려움
  • 예측 값과 실제 값의 오차가 존재할 것으로 예상
  • 예측 값과 실제 값이 비슷할 수록 좋은 모델임
  • 오차로 모델 성능 평가

$y$: 실제값

• 우리가 실제로 예측하고 싶은 값 (target)
• 오차는 이 값과 예측 값의 차이

$\hat{y}$: 예측값

• 이미 알고 있는 평균으로 예측한 값
• 우리 모델의 예측값이 평균값보다 오차를 얼마나 더 줄였는지가 중요

$\bar{y}$: 평균값

• 우리 모델로 새롭게 예측한 값
• 평균값 보다 얼마나 잘 예측했는지 중요

(1) 회귀 모델 성능 평가

• 회귀모델의 성능은 실제값과 예측값의 차이인 오차의 크기로 평가한다.
• Error의 값이 작아야 모델의 성능이 좋은 것이다.

1) SSE (Sum Squared Error)

$\large SSE=\frac{}{}\sum_(y-\hat{y})^2$

• 오차 제곱의 합

2) MSE (Mean SSE)

$\large MSE=\frac{1}{n}\sum(y-\hat{y})^2$

• 오차 제곱의 합의 평균

# 함수 불러오기 
from sklearn.metrics import mean_squared_error

# 평가하기
print('MSE: ', mean_squared_error(y_test, y_pred))

3) RMSE (Root MSE)

$\large RMSE=\sqrt{\frac{1}{n}\sum(y-\hat{y})^2}$

• 오차제곱의 합의 제곱근

# 함수 불러오기 
from sklearn.metrics import mean_squared_error

# 평가하기
print('RMSE: ', mean_squared_error(y_test, y_pred) ** 0.5)
# 같은 방법임
print('RMSE: ', mean_squared_error(y_test, y_pred, squared=False))

4) MAE : (Mean Absolute Error)

$\large MAE=\frac{1}{n}\sum|y-\hat{y}|$

# 함수 불러오기 
from sklearn.metrics import mean_absolute_error

# 평가하기
print('MAE: ', mean_absolute_error(y_test, y_pred))

5) MAPE (Mean Absolute Percentage Error)

$\large MAPE=\frac{1}{n}\sum\left |\frac{y-\hat{y}}{y}\right |$

# 함수 불러오기 
from sklearn.metrics import mean_absolute_percentage_error

# 평가하기
print('MAPE: ', mean_absolute_percentage_error(y_test, y_pred))

오차를 바라보는 다양한관점

SST: Sum squared Total(전체오차)

• 실제값 - 평균값

SSR: Sum squared Regression(전체오차 중 회귀식이 잡아낸 오차)

• 예측값 - 평균값

SSE: Sum squared Error(전체 오차 중 회귀식이 잡아내지 못한 오차)

• 실제값 - 예측값

SST = SSE + SSR

6) $R^2$ (R-Squared)

• 전체 오차 중에서 회귀식이 잡아낸 오차비율 (0~1사이)
• 오차의 비 또는 설명력이라 부른다
• $R^2$ = 1 이고 MSE=0 이면 모델이 완벽하게 학습한 것이다.
• 클수록 좋다

# 함수 불러오기 
from sklearn.metrics import r2_score

# 평가하기
print('R2: ', r2_score(y_test, y_pred))

score 메서드

• 회귀모델에서 score메서드 사용시 r2 모델과 같음

# 참고: score 메서드 사용 r2와 같음
model.score(x_test, y_test)

(2) 분류 모델 성능 평가

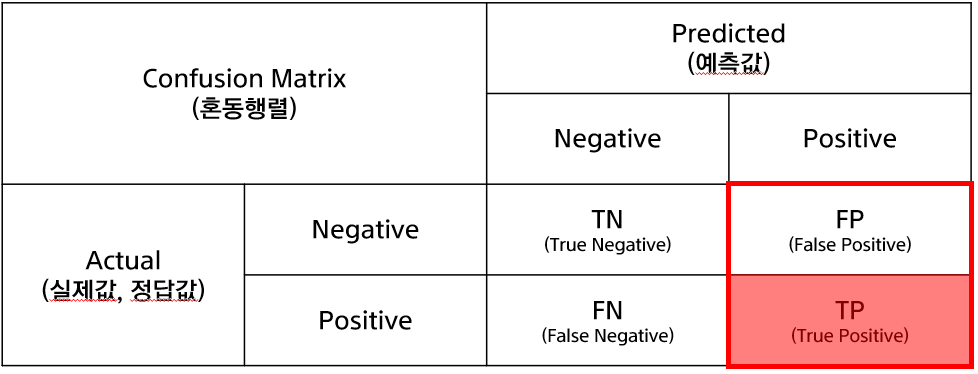
• 혼동행렬(Confusion Matrix): 정확도, 정밀도, 재현율을 확인 할 수 있는 지표
• 정확도(Accuracy): True(1), False(0)을 정확히 예측한 비율
• 정밀도(Precision): 예측한 것 중 True(1)인 비율
• 재현율(Recall): 실제 True(1)인 것을 True(1)라 예측한 비율

1) 혼동행렬(confusion Matrix)

# 모듈 불러오기
from sklearn.metrics import confusion_matrix

# 성능 평가
print('혼동행렬:\n',confusion_matrix(y_test, y_pred))

# 혼동행렬 시각화
plt.figure(figsize=(5,3))
sns.heatmap(confusion_matrix(y_test, y_pred),
           annot=True,
           cmap='Blues',
           cbar=False,
           annot_kws={'size':15})

plt.show()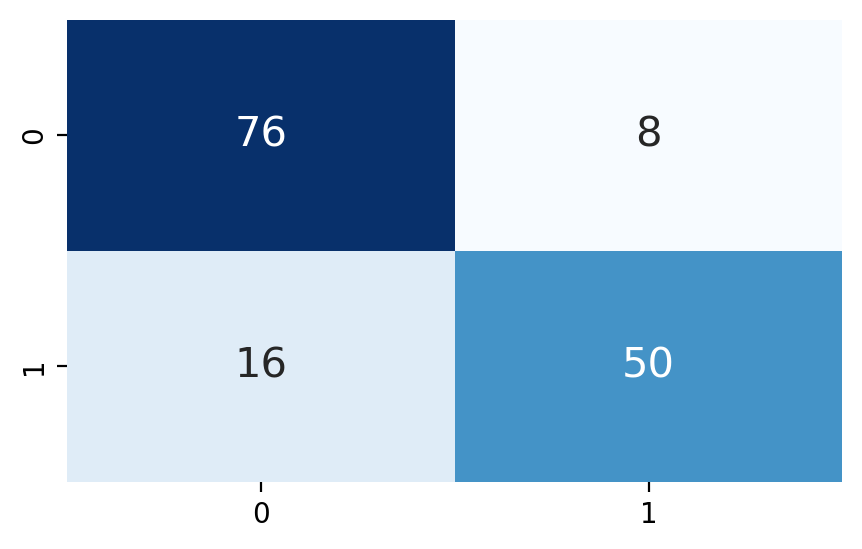

2) 정확도(Accuracy)

• $\large Accuracy = \frac{TP+TN}{TP+TN+FP+FN}$
• 정분류율
• 전체 중 정확히 예측한 TN + TP 비율

# 모듈 불러오기
from sklearn.metrics import accuracy_score

# 성능 평가
print('정확도:', accuracy_score(y_test, y_pred))

score 메서드

• 분류모델에서 사용 시 정확도(acc)와 같음

# 참고: 평가 성능 (정확도)
model.score(x_test, y_test) 
>
0.84

# 참고: 학습 성능 (정확도)
model.score(x_train, y_train)
>
0.8885714285714286

• 위 결과 처럼 학습 성능이 좋은데 평가 성능이 떨어지면 과대적합 이다.

3) 정밀도(Precision)

• $\large Precision = \frac{TP}{TP+FP}$
• positive로 예측한 것 중 TP인 비율

# 모듈 불러오기
from sklearn.metrics import precision_score


# 성능 평가
# 기본
print('정밀도: ',precision_score(y_test, y_pred))

# 이진분류라 생각하고 1에 대한 precision 출력
print('정밀도: ',precision_score(y_test, y_pred, average='binary'))

# 0 과 1 일때 둘다 출력
print('정밀도: ',precision_score(y_test, y_pred, average=None))

# 평균
print('정밀도: ',precision_score(y_test, y_pred, average='macro'))

# 가중치 평균
print('정밀도: ',precision_score(y_test, y_pred, average='weighted'))

4) 재현율(Recall)

• $\large Recall = \frac{TP}{TP+FN}$
• 실제 positive인 것 중 TP인 비율

# 모듈 불러오기
from sklearn.metrics import recall_score

# 성능 평가
print('재현율: ',recall_score(y_test, y_pred, average=None))

5) F1-Score

• $\large F1 = \frac{2\times Precision\times Recall}{Precision+Recall}$
• 정밀도와 재현율의 조화 평균
• 관점이 다른 경우 조화 평균이 의미가 있음

# 모듈 불러오기
from sklearn.metrics import f1_score

# 성능 평가
print('f1: ',f1_score(y_test, y_pred, average=None))

6) Classification Report

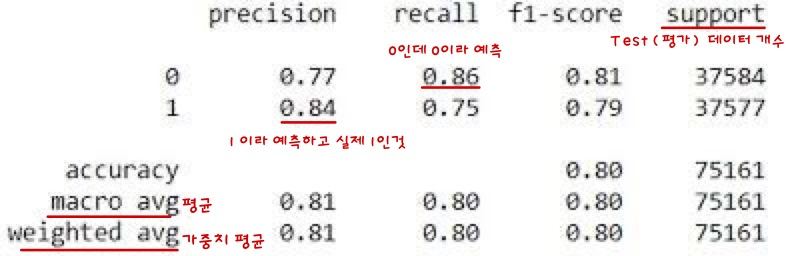
# 모듈 불러오기
from sklearn.metrics import classification_report

# 성능 평가
print(classification_report(y_test, y_pred))