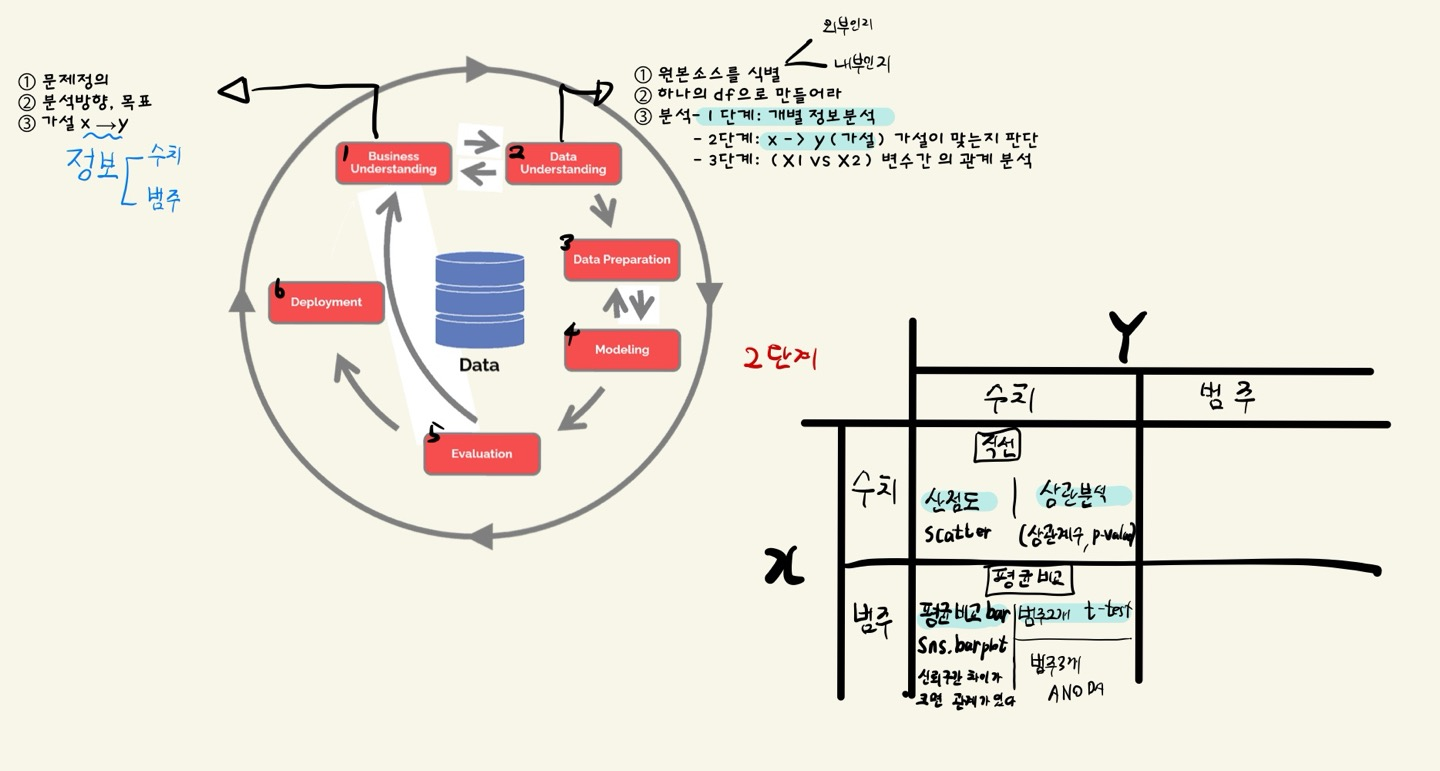
• 오늘도 CRISP-DM 그림으로 시작한다. (악필 양해조옴....)
• CRISP-DM의 단계중 2단계 가설이 맞는지 판단하는 연습을 많이 했다.
• 그 가설을 판단하려면 피쳐x(수치) -> 타겟y(수치)에서 직선이 표현되는지가 중요하다.
  • 그래프의 산점도(scatter)를 통해 직선이 그려지는지 볼 수 있다.
  • 상관계수와 p-value(유의수준)을 통해 얼마나 변수와 타겟 간의 관계가 있는지 알 수 있다.
• 무슨 소리하는지 모르겠다고? 나도 수업 시간에 그랬다. 다시 한번 생각해보는 시간이 되겠다.

1. 가설검정

(1) 가설과 가설검정

• 모집단: 우리가 알고싶은 대상 전체 영역
• 표본: 그 대상의 일부 영역

  ex) x->y 라는 가설을 만들면 아래와 같이 생각한다.

  • x에 따라 y가 차이가 있다.
  • x와 y는 관계가 있다.
  • x에 따라 y는 변한다.

• 가설을 검증하기 위해 모든 것을 전수조사를 할 수 없기 때문에 표본을 추출하여 분석을 한다.
• 표본으로 부터 분석을 한 뒤 모집단에도 맞을 것 이라 주장한다.

(2) 통계적 검정

귀무가설($H_0$) : 기존의 가설, 영가설, 보수적인 입장
대립가설($H_1$) : 새로운 가설, 연구가설, 내가 바라는 바

• 만약 내가 'x가 y일거야'라고 가설을 만든다면
• 대립가설은 'x가 y일거야'
• 귀무가설은 'x가 y가 아닐거야'

분포 + 판단 기준

• x와 y의 차이 값을 구했지만, 거기에 대한 기준이 없다.
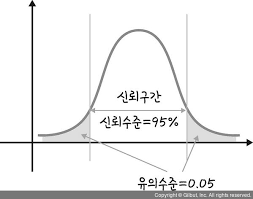
• 그 기준을 판단하는 것을 유의수준(p-value) 이라한다.
• 유의수준(p-value) 은 0.05 보다 작아야 차이가 있다고 판단한다.
• 유의 수준에는 단측검정, 양측 검정이 있다.

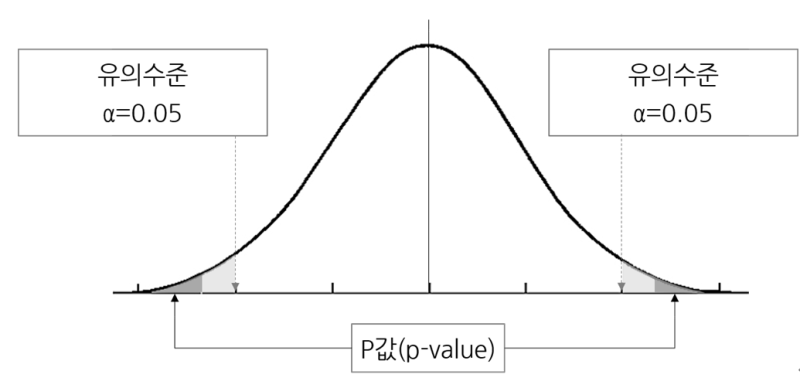
• 위 그림의 그래프 내의 넓이는 1이다.
• 짙게 칠해진 부분이 p-value
• 옅게 칠해진 범위가 유의수준 0.05이다.
• 저 데이터에 대한 p-value는 0.05보다 작으므로 차이가 있다 라고 보면 된다.
• 검정 통계량에는 t통계량, $x^2$(카이제곱)통계량, f통계량이 있다.

2. 이변량 분석1 (숫자->숫자)

• x(수치형 변수) -> y(수치형 변수) 를 분석할 때
• 직선, 선형, linear 를 기반으로 (직선에 모여있는지, 직선으로 나오는지)
• 산점도 분석 과 상관분석 을 한다.
  
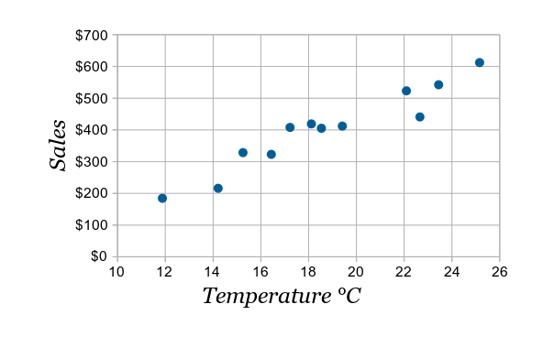
• 이 그림 처럼 ' 직선 이 보이는 가?' 를 도출하는 것이 중요하다.
• 생각보다 쉽지 않을 것이다.

(1) 시각화(산점도)

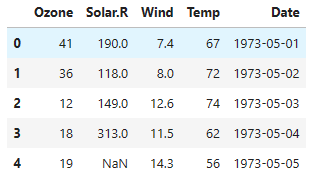
이런 한 값을 가지는 air라는 데이터프레임이 있다.

예시( 모두 동일하게 나옴
plt.scatter(air['Temp'], air['Ozone'])

plt.scatter('Temp', 'Ozone', data = air)

sns.scatterplot(x='Temp', y='Ozone', data = air)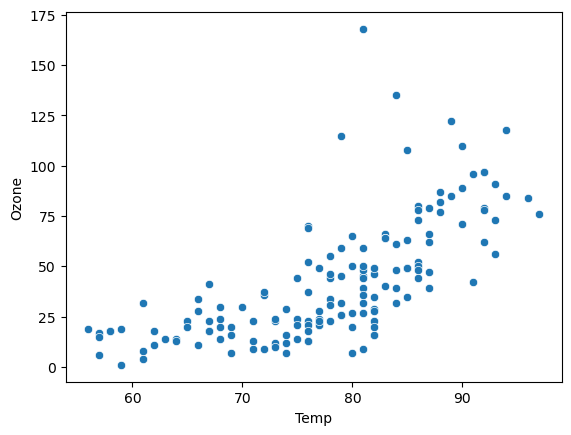

• 산점도가 나온다.
• 이 그래프를 보면 양으로 증가하는 직선이 보일 것이다.
• 강의 시간에 그래프를 그리는 것도 좋지만 더 중요한건 분석하는 거라고 한기영 강사님께서 말씀하셨다.
• 분석을 한번 해보자

X ('Temp', 'Wind', 'Solar.R') -> Y ('Ozone')이라 가설을 설정한다.

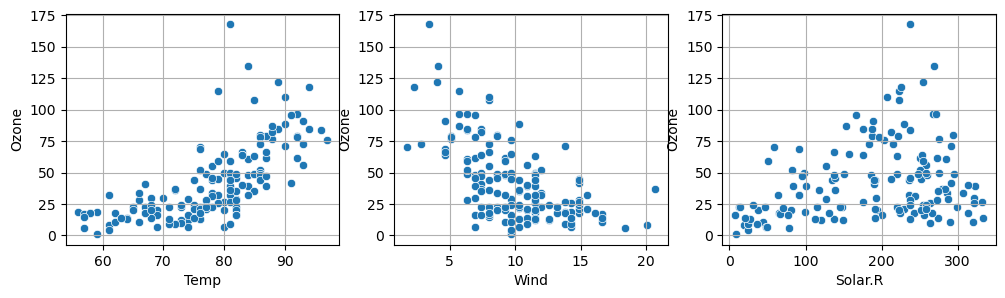
• 세개의 변수 중 Ozone과 가장 강한 관계를 가지는 것은 Temp이다.
• 이를 통해 더 자세한 분석을 진행할 수 있을 것이다.

• 상관관계는 직선 에 가까울 수록 강한 상관관계가 된다.
• 기울기 는 상관관계에 영향을 끼치지 않는다.
• 대신, 다른 관계가 있다는 것을 인지 해야한다.

다른 함수

sns.pairplot(dataframe) # 숫자형 변수에 대한 산점도를 한번에 그려줌

• 변수와 데이터가 많으면 시간이 걸리고, 확인하기 어려움

sns.jointplot(x, y, data=): 산점도와 히스토그램 동시 출력
sns.regplot(x, y, data=): 산점도와 임의의 직선 동시 출력

(2) 수치화(상관분석)

• 그래프를 보고 파악하는 것은 어렵다.
• 이를 보완하기 위한 방법은 수치화하여 가설을 검증한다.
• 상관관계는 두 변수간의 종속적인 관계를 나타낸다.
• 이는 그 변수간 상호적인 관계가 있는지 나타내는 것이다.

상관계수(r)

• -1 ~ 1 사이 값
• 상관계수끼리 비교 가능
• -1, 1에 가까울 수록 강한 상관관계를 나타낸다.
• 0에 가까우면 약한 상관관계

import scipy.stats as spst
spst.pearsonr(x='Temp', y='Ozone', data=air)

PearsonRResult ( statistic =0.6833717861490114, pvalue =2.197769800200284e-22)

• 결과: (상관계수, p-value) 튜플 형태로 출력
• 상관계수가 0.68정도로 직선에 가까운 편이다.
• p-value가 2.19에 10의 -10승이다.
• 주의점: 피어슨 상관분석시 값에 NaN이 있으면 결과가 NaN으로 나온다.
• .notnull()로 NaN을 없애주어야 한다.

• p-value < 0.05 두 변수 간의 관계가 있다.
• p-value <= 0.05 두 변수 간의 관계가 없다.

• 상관계수는 직선의 관계만 수치화 해준다.
  • 고려하지 않은 직선의 기울기, 비선형 관계도 생각하고 데이터 분석을 실시하여야 한다.

다른 함수

dataframe.corr(): 모든 숫자형 변수 들간의 상관계수 계산

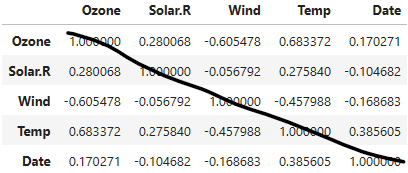
• 대각선은 무시하고
• 아래나 위 둘 중 하나만 보면 된다.

heatmap(): 상관계수 시각화

sns.heatmap(air.corr(), 
            annot = True,            # 숫자(상관계수) 표기 여부
            fmt = '.3f',             # 숫자 포멧 : 소수점 3자리까지 표기
            cmap = 'RdYlBu_r',       # 칼라맵
            vmin = -1, vmax = 1)     # 값의 최소, 최대값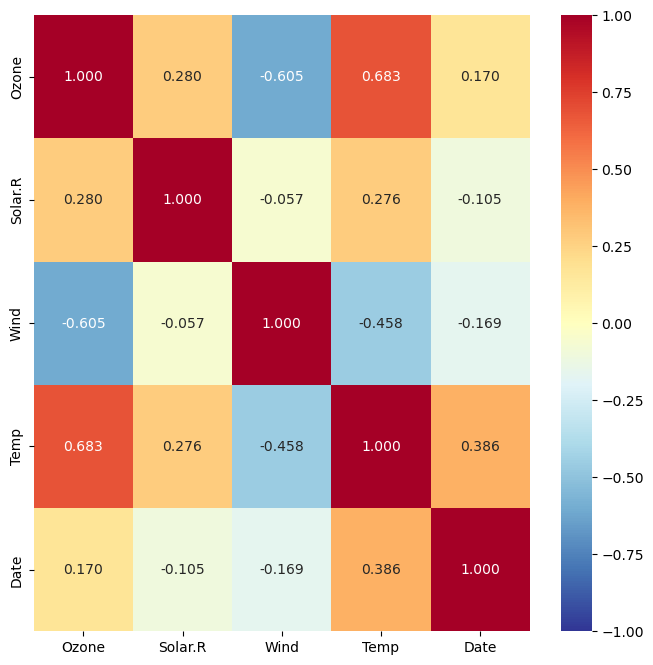

3. 평균 추정과 신뢰구간

(1) 평균, 분산, 표준편차

• 대표값을 평균으로 설정
• 분산: 평균으로 얼마나 벗어나 있는지 나타내는 값(이탈도)
• 표준편차: 분산과 같은 개념임 (루트를 씌운 값)
  (추가) 표준오차: 모평균과 표본평균의 오차

(2) 모집단과 표본

• 포본조사
  • 추출 방식: 많은 수, 무작위
  • 장점: 적절한 비용, 적절한 시간
  • 단점: 오차가 존재함

• 전수조사
  • 모집단(전체)을 조사
  • 장점: 정확하고, 오차가 0임
  • 단점: 비용과 시간이 많이 나옴

(3) 표본평균과 모평균

• 표본을 뽑는 목적(sampling) -> 모집단 추정
• 표본평균을 구했다는 것은 모평균을 구하기 위한 것이다.
• 표본평균
  • 표본평균을 통해 모평균에 대한 추정치 가 있음
  • 추정치에는 오차 가 있음( 표준오차 )

(4) 중심극한정리

Ex )

• 전국 고등학생 50명을 무작위로 뽑아 평균을 계산한다.
• 같은 방법으로 100번 반복하여
• 50명씩 뽑은 데이터를 평균한 값 100개를 얻을 수 있다.

• 이 100개를 평균을하면 정규분포 가 나타남
• 여기서 표본의 크기가 클수록 정규분포 모양이 뾰족하고 좁은 형태가 된다. 즉, 데이터의 건수가 많은 경우에 정규분포가 뾰족한 모양(좁은 형태)이 된다.

(5) 95% 신뢰구간

• 표준오차를 바탕으로 95% 확률 구간을 구할 수 있음
• 표본을 100번 정도 뽑으면 95번 정도는 95% 신뢰구간 안에 모평균이 포함한다. (5개 정도는 벗어난다)

  $x_1$, $x_2$, $x_3$ .... $x_n$에서
  각 $x_n$의 평균에는 각각 신뢰구간이 있다.
  이 신뢰구간을 100번 중 95번은 95% 신뢰구간 안에 포함하게 된다.

4. 이변량 분석2 (범주->숫자)

-수치형 변수 vs 범주형 변수 구분하는 방법

• barplot
• 범주가 2개일 때 (두 평균 차이)
• 범주가 3개일 때 (전체 평균과 각 범주의 평균 비교)

• 이 변수를 가진 titanic 데이터로 해보자

(1) 시각화 (barplot)

sns.barplot(x="Survived", y="Age", data=titanic)
plt.grid()
plt.show()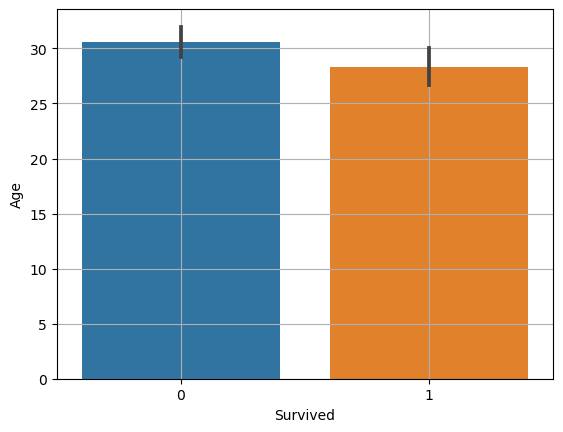

• 신뢰구간은 짧을수록 평균 값이 믿을만 하다.
• 대립가설이 맞다는 경우
  • 평균 차이가 클 때
  • 신뢰구간은 겹치지 않을 때

• 생존/사망 여부의 범주형 변수와 나이별 수치형 변수와 관계를 나타낸다.
• 이 그래프를 해석하면 평균과 신뢰구간 차이가 거의 없고, 신뢰구간이 겹친다.
• 그러므로 대립가설이 틀리다.

(2) 수치화

• t-test: 두 그룹 간 평균에 차이가 있는지
• anova: 3개 이상, 전체 평균과 각 그룹 평균에 차이가 있는지?

t-test

• t통계량: 두 그룹의 평균 간 차이를 표준오차로 나눈 값
  • p-value가 0.05 보다 작으면 차이가 있다.
  • t통계량이 -2 ~ +2 사이가 아니라 바깥에 있으면 차이가 있다고 본다.(파란색 색칠된 부분)
    

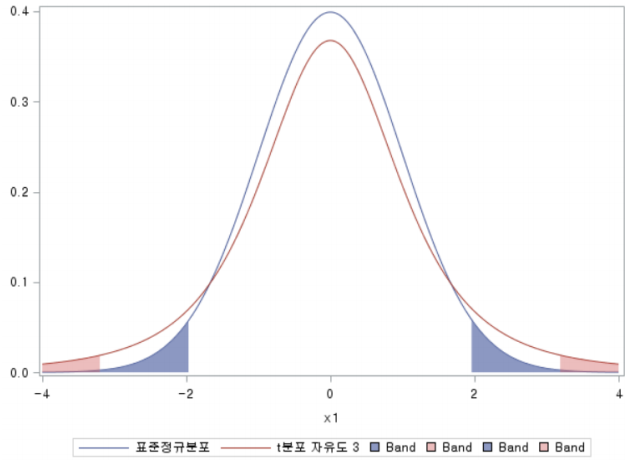
사용방법

• titanic 데이터를 사용
• 귀무가설: 타이타닉 탑승객 생존 여부별 나이의 차이가 없다
• 대립가설: 생존여부에 따른 나이의 차이가 있다.

#NaN행 제외 후 temp변수에 저장
temp = titanic.loc[titanic['Age'].notnull()] #NaN행 제외 후 temp에 담음

# 두 그룹으로 데이터 저장
died = temp.loc[temp['Survived']==0, 'Age']
survived = temp.loc[temp['Survived']==1, 'Age']

spst.ttest_ind(died, survived)

TtestResult(statistic=2.06668694625381, pvalue=0.03912465401348249, df=712.0)

• t통계량: 2.066
• p-value: 0.0391

• t통계량이 2보다 크므로 차이가 있지만, 크지는 않다.
• p-value는 0.05보다 작지만, 크지는 않다.
• 조금의 관계가 있다.

ANOVA(분산분석)

• 한기영 강사님께서 우리가 통계 부분을 어려워해서 이 부분은 내일 나가기로 했다. 감사합니다 강사님~~~ 덕분에 앞에 복습하면서 이해가 된 것 같습니다. 이 글을 보신다면 감사합니다 정우성님 ㅎㅎ

• t-test로 두 그룹 간 평균 차이를 구했다.
• 이제 3개 이상의 그룹이 있다면 어떻게 하겠는가?
• ANOVA(분산분석)을 사용해야 한다.
• 기준은 전체의 평균으로 두고 봐야한다.
• F통계량, 분산비 라고도 한다.

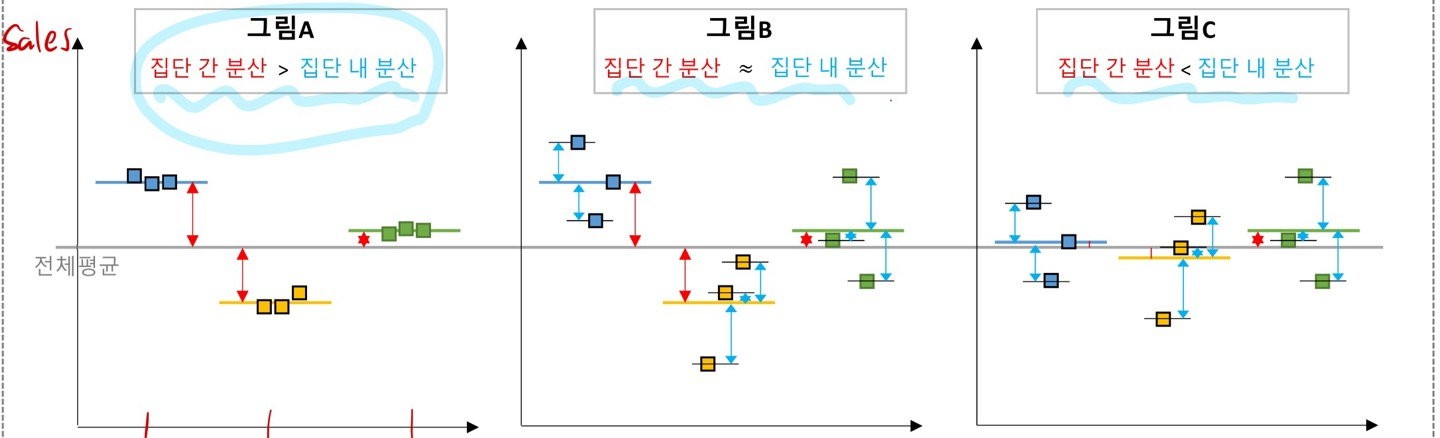
A, B, C 세개의 집단이 있다고 가정하자.
A, B, C 전체의 평균을 기준으로 하여 각각 비교하여 분석하는 것이다.

• 이 그림처럼 각 관계가 집단 간 분산 > 집단 내 분산 의 크기 관계가 가정 이상적인 관계다.

titanic.Embarked.unique()  # 값 확인 하기

titanic.isna().sum() # NaN 값 확인

temp = titanic.loc[titanic['Pclass'].notnull()] # NaN값 제거 후 temp에 저장

# 각 변수에 저장
P_1 = temp.loc[temp['Pclass'] == 1, 'Fare']
P_2 = temp.loc[temp['Pclass'] == 2, 'Fare']
P_3 = temp.loc[temp['Pclass'] == 3, 'Fare']

spst.f_oneway(P_1, P_2, P_3)
f_oneway(A, B, C)


>
F_onewayResult(statistic=57.443484340676214, pvalue=7.487984171959904e-24) # F통계량, pvalue 값 도출

• f통계량은 2나 3 이상이면 차이가 있다고 판단한다.
• 분산분석은 전체 평균대비 각 그룹간 차이가 있는지만 알려준다. (전체평균, A) (전체평균, B) (전체평균, C)
• 어느 그룹간에 차이가 있는지 알 수 없음 (A, B) (B, C), (A, C)