미리 알아야 하는 지식- 표(tabular)의 기반한 해결법
상태들이 discrete할때의 해법들에 대해서는 DP, TD방법 등을 이용하여 해결 가능하며, 이론상 최적 정책을 찾을수 있다.
하지만 위 방법은 규모가 큰 문제에 대해서 계산량의 이유로 사용이 불가능하다.
좌표(x,y)와 같이 상태, 행동이 연속적인 값을 가질때의 해결 방법 또한 필요하다.
(discrete할때를 포함하는 일반화된 방법)
따라서 근사적 해법을 사용해야 한다.
방법:
정책: 가치에 대해 탐욕적(greedy)으로 선택
가치를 근사하는 다양한 방법: 인공신경망, 트리기반 알고리즘 등
정책을 실행해가며 가치를 측정(ex: TD방법), 인공신경망을 학습하는 방식 등으로 가치를 근사
기존방법은 가치를 측정한 후 대응되는 가치함수의 값을 바로 업데이트 해주었다면,
근사적 해법에서는 가치를 근사하는 w 등의 가중치를 업데이트해준다.
위 큰 틀에서 속도와 정확도를 향상시키는 다양한 방법에 대해 공부하면 됨.
가치근사
선형방법
상태 s를 기저함수의 집합에서 몇개 골라서 특징벡터x로 변환한다.
x를 하나의 실수로 대응하기 위한 가중치 w를 설정하고,
x와 w를 내적하는 방식으로 가치함수를 정의한다.
이때 w가 지역최저라면 전역최저가 보장됨 <- w의 각 가중치들이 독립적이기 때문
타일부호화
뒷부분에서 설명
인공신경망
설명이 필요합니까
등등
특징 전처리
다항식
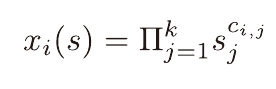
(x1,x2)를 (1, x1, x2, x1*x2)와 같이 변환하는 알고리즘이다.
k는 변환 전 특징의 차원 수이다.
i는 변환 후 특징의 차원 수로 미리 설정해주어야 하고 Ci,j를 미리 정의해둬야 한다.
위 예시에서는
c0,1 = 0
c0,2 = 1
c1,1 = 0
c1,2 = 1 인 경우이다.
푸리에 기저
푸리에 변환을 보면 코사인으로 여러가지 모양을 만들수 있다.
다항특징을 쓰는 이유는 각 변수, 변수들간의 관계에서 비롯된 가치가 비선형적인 경우를 고려하기 위함이다.
푸리에 특징을 쓰는것도 한가지 전략이 될 수 있음을 알 수 있다.
푸리에 변환은 분해를 하는것이지만, 이 방법은 분해보다는 합치는 원리를 이용한다.
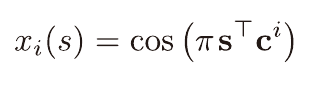
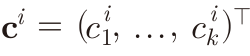
이번에도 c를 미리 정의해두어야 한다.
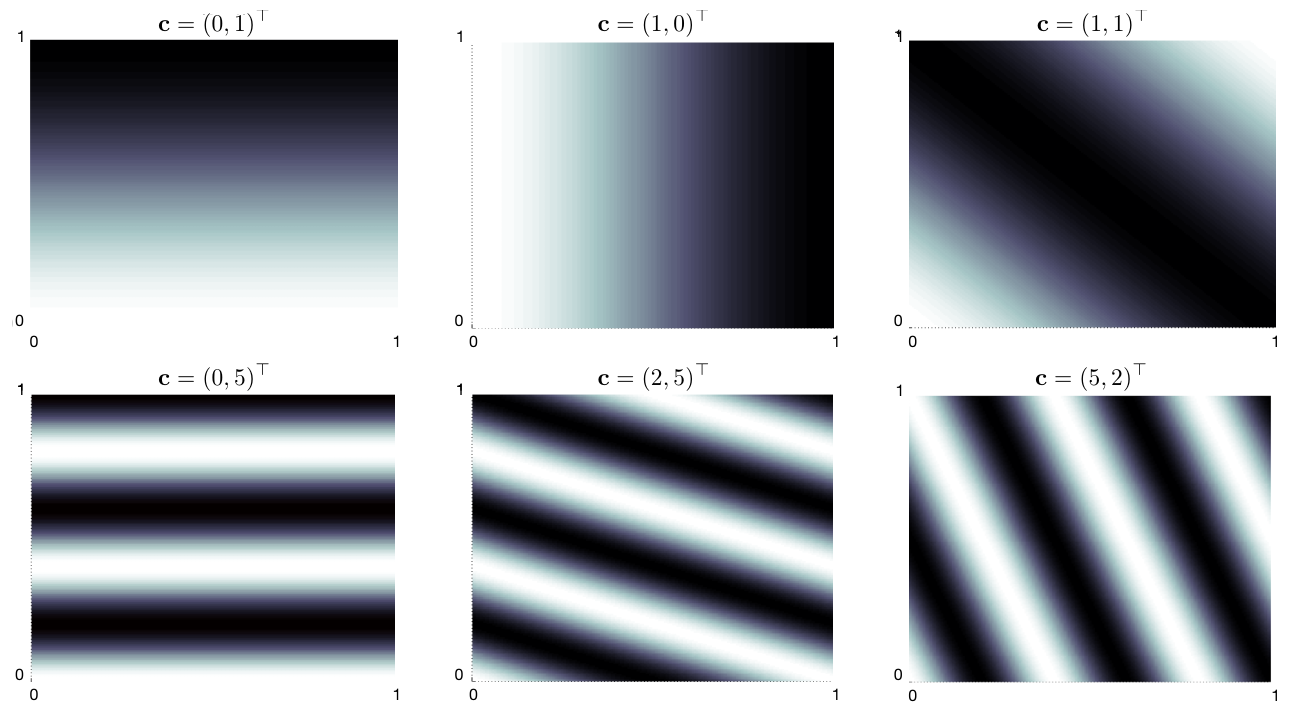
k가 2일때의 c에 따른 코사인 값의 분포
위 전처리를 마친 후 선형방법으로 가치 근사를 하는 경우에 각 wi에 해당하는 시간간격을 wi 대응되는 ci의 진동수와 반비례하게 설정하는것이 도움이 된다.
특정 파장을 분해했을때 진동수가 클수록 계수가 작을확률이 크기 때문으로 추측된다.
타일부호화
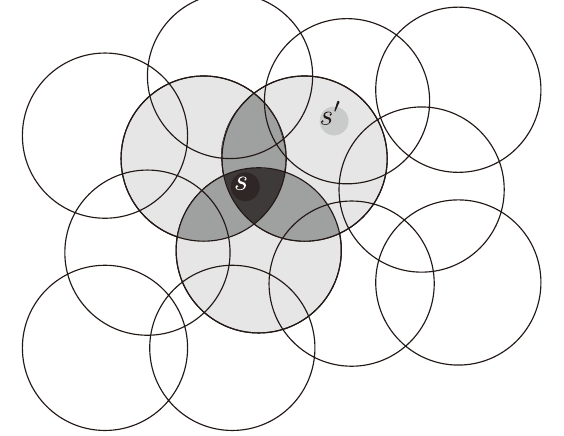
원, 사각형 등등의 타일을 공간에 뿌린 뒤
각 점들이 타일에 포함되면 1, 아니면 0을 가지도록 하는 방식으로 특징 전처리를 한다.
(타일의 수가 64개라 치면 x(s)의 크기는 64)
타일마다 가중치 wi를 하나씩 가지고 있으며, 이 둘을 내적하여 가치를 계산한다.
