[Paper Review] Continual Learning Through Synaptic Intelligence, PMLR 2017

박수영·2024년 3월 4일

Continual Learning

목록 보기

1/2

시작하기에 앞서

Continual Learning Through Synaptic Intelligence [1] 논문을 읽고 정리한 포스팅입니다.
개인적인 해석이 일부 들어있습니다.

Background

Source: Artificial Neural Networks and its Applications - GeeksforGeeks

Artificial Neural Networks (인공신경망, 이하 ANN) 와 Biological Neural Networks (생물학적 신경망, 이하 BNN) 의 차이가 있다면, catastrophic forgetting (파괴적 망각 현상) 문제에 대해 대처할 수 있는지 그 여부가 있겠습니다.
Catastrophic forgetting 이란, 서로 다른 task 를 학습하는 과정에서 이전 task 에 대해 학습한 정보를 까먹는 현상을 말합니다. 예를 들면 국어를 공부하다가 수학을 공부하는 경우, 이전에 국어에 대해 공부한 내용을 까먹는 것이라고 할 수 있겠습니다.
본 논문에서는 이러한 차이가 생기는 이유로 complexity of synapses, 즉 시냅스들의 복잡도를 언급합니다.
Synapse 라 함은 서로 다른 neurons 간에 전기적 신호를 주고 받는 접점을 말하는데요. ANN 의 경우 하나의 synapse 가 single scalar quantity, 즉 단일 스칼라 값으로 표현되지만 BNN 의 synapse 는 시공간적 정보를 표현할 수 있을 정도로 복잡하고 정교한 체계를 갖추고 있습니다.
위 그림에서 왼쪽은 BNN 을, 오른쪽은 ANN 을 표현하고 있습니다. 왼쪽 그림에서 Dendrites 는 입력을 받는 부분이고, Axon 은 결과를 출력하는 부분입니다. Synapse 는 서로 다른 neuron 의 dendrites 와 axon 이 만나는, 그 접점을 얘기합니다.
BNN 의 경우 synapse 가 복잡하고 정교한 체계를 갖추고 있지만, ANN 의 경우 오른쪽 그림을 보시면 알 수 있다시피 single scalar quantity 로만 표현하는 모습입니다.
따라서 본 논문은 BNN 의 synapse 가 가지는 복잡하고 정교한 체계를 ANN 의 synapse 에 일부 구현함으로써 catastrophic forgetting 문제를 완화하고자 하였고, 어느 정도 성공했다고 주장합니다.

Key idea

Source: figure 3 - ref. [1]

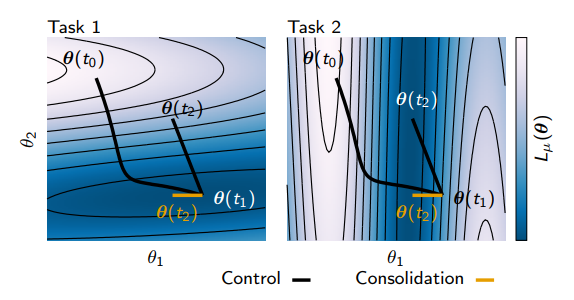
위 이미지를 통해 논문의 핵심 아이디어를 추상적으로 이해할 수 있습니다.
Task 1, Task 2 는 서로 다른 작업입니다. 여기서 서로 다른 작업이란, 작업의 목적이 다르다는 것을 의미합니다. 예를 들어 Task 1 은 0과 1을 분류하는 작업이고, Task 2 는 2와 3을 분류하는 작업이라면, Task 1 과 Task 2 는 서로 다른 작업이라고 정의할 수 있습니다.
Contour plot (등고선 그래프) 은 task 별 loss surface 를 표현합니다. 색상이 어두울수록 loss 가 낮고, 밝을수록 loss 가 높다는 것을 나타내고 있습니다.
이를 바탕으로 위 figure 를 해석해보겠습니다.

가장 먼저 Task 1 을 학습해봅시다. $\boldsymbol\theta({t_0})$ 는 $t=t_0$ 일 때, 즉 시작 parameters 를 의미합니다. 일반적인 gradient descent algorithm (경사하강법) 을 사용하여 모델을 최적화 (학습) 하게 되면, loss 가 낮은 지점인 $\boldsymbol\theta({t_1})$ 으로 parameters 가 업데이트 됩니다. $\boldsymbol\theta({t_0})$ 와 $\boldsymbol\theta({t_1})$ 을 잇는 굵은 선은 Task 1 학습 과정에서 변화한 parameters의 trajectory 를 의미합니다.

이어서 Task 2 를 학습해보겠습니다. Task 1 을 학습하는 과정에서 model parameters 는 $\boldsymbol\theta({t_1})$ 으로 이동했습니다. 따라서 Task 2 의 시작 parameters 는 $\boldsymbol\theta({t_1})$ 입니다.
Task 2 training data 에 대해 최적화하는 과정에서 model parameters 는 $\boldsymbol\theta({t_2})$ 로 이동하게 됩니다. $\boldsymbol\theta({t_1})$ 과 $\boldsymbol\theta({t_2})$ 를 잇는 굵은 선은 Task 2 학습 과정에서 변화한 parameters의 trajectory (궤적, 발자취) 를 의미합니다.

Task 1 부터 Task 2 까지 순차적으로 학습한 결과, model parameters 는 $\boldsymbol\theta({t_2})$ 가 되었습니다.
$\boldsymbol\theta({t_2})$ 는 Task 2 를 해결하는 것에 있어 최적의 parameters 입니다. 하지만 Task 1 에게는 최적의 parameters 가 아닐 확률이 높습니다. Task 2 를 학습하는 과정에서 Task 1 은 전혀 고려하지 않았기 때문입니다. 왼쪽의 contour plot 을 보면, model parameters 가 $\boldsymbol\theta({t_2})$ 로 이동하면서 loss 값이 높아졌다는 것을 알 수 있고, 이는 $\boldsymbol\theta({t_2})$ 가 Task 1 에서 최적의 parameters 가 아니라는 것을 나타내고 있습니다.
$\boldsymbol\theta({t_2})$ 처럼 Task 1, 2 모두에 대해 준수한 성능을 보이는 parameters 도 존재할 수 있는데, 어떻게 하면 이를 찾을 수 있을까요?

본 논문에서는 task training 과정에서 추적할 수 있는 parameter trajectory 를 활용한다면, 여러 개의 task 모두에 대해 준수한 성능을 보장하는 parameters 를 찾는 것이 가능하다고 주장합니다.
어떻게 해서 가능한 것인지, 아래 Details 에서 자세히 설명해보도록 하겠습니다.

Details

가장 먼저 해야할 것은, 지난 task 학습 과정에서 기록한 parameter trajectory 를 이용하여 loss 에 대한 gradient $\boldsymbol{g} = \frac{\partial{L}}{\partial{\boldsymbol{\theta}}}$ 를 계산하는 것입니다. 왜냐하면 $\boldsymbol{g}$ 는 parameters 의 변화가 loss 의 변화에 미치는 영향에 대한 정보를 담고 있기 때문입니다. 이를 수식으로 나타내면 아래와 같습니다.

\tag{1} L(\boldsymbol\theta(t) + \boldsymbol\delta(t)) - L(\boldsymbol\theta(t) \approx \sum_k{g_k(t)\delta_k({t})}

$\boldsymbol{\delta}(t)$ 는 time 이 $t$ 일 때 parameter 의 미소 변화량, 즉 $\frac{\partial{\boldsymbol\theta}}{\partial{t}}$ 을 의미합니다. $k$ 는 전체 parameter 개수를 의미하므로, $g_k(t)$ 와 $\delta_k(t)$ 는 time (또는 step) 이 $t$ 일 때 $k$ 번째 parameter 의 gradient 와 미소 변화량을 의미합니다.
이를 바탕으로 수식 (1)을 해석해보자면, parameters $\boldsymbol\theta(t)$ 를 $\boldsymbol\delta(t)$ 만큼 아주 조금 변화시켰을 때 loss 에 생기는 총 변화량은 (좌변), 각 parameter 의 gradient 와 미소 변화량을 곱한 것의 총 합으로 approximation (근사) 할 수 있다는 것입니다.

다음으로 계산해야할 것은 전체 trajectory 에 대한 loss 의 변화량을 계산하는 것입니다. 이는 시작 지점 $t_0$ 부터 도착 지점 $t_1$ 까지의 parameter trajectory 를 따라 적분을 계산하면 구할 수 있습니다. 수식은 아래와 같습니다.

\tag{2} \int_C{\boldsymbol{g}(\boldsymbol{\theta}(t))}d\boldsymbol{\theta} = \int_{t_0}^{t_1}{\boldsymbol{g}(\boldsymbol{\theta}(t))} \cdot \boldsymbol{\theta}^{\prime}(t)dt

풀어서 설명하자면, 수식 (2)는 $t_0$ 부터 $t_1$ 구간 전체에 대해 parameter 가 loss 에 미치는 영향을 나타내고 있습니다.
수식 (1)과 (2)를 결합하면, parameter trajectory 에서 발생한 전체 loss 에 개별 parameter 가 미치는 영향을 계산할 수 있게 되는데요. 이를 일반화하여 수식으로 나타낸다면 아래와 같습니다.

\begin{aligned} \int_{t^{\mu-1}}^{t^{\mu}}{\boldsymbol{g}(\boldsymbol{\theta}(t))} \cdot \boldsymbol{\theta}^{\prime}(t)dt &= \sum_{k} \int_{t^{\mu-1}}^{t^{\mu}}{g_k({\theta}(t))}\theta^{\prime}_{k}(t)dt\\ \end{aligned}

\tag{3} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\equiv -\sum_k{\omega^{\mu}_k}

$\mu$ 는 현재 task 를 의미합니다. 즉 수식 (3)은 이전 task 학습을 마친 지점 ( $t^{\mu-1}$ ) 부터, 현재 task 학습을 마친 지점 ( $t^{\mu}$ ) 사이 구간에서 발생한 전체 loss 에 대해 개별 parameter 가 미치는 영향을 의미합니다. 쉽게 얘기하면 task $\mu$ 를 학습하는 과정 동안 개별 parameter 가 미친 영향력을 수치로 나타낸 것입니다.
수식 (3)에 마이너스 부호가 붙은 것은 최적화 과정에서 $\omega^{\mu}_{k}$ 를 최소화해야 한다 (값을 키워야 한다) 는 것을 의미합니다.
뒤에서 자세히 설명하겠지만, 본 논문에서는 parameter importance 라는 것을 정의하여 parameter 별로 업데이트 정도를 조절합니다. Importance 가 낮은 parameter 는 업데이트를 많이 하고, importance 가 높은 parameter 는 업데이트를 적게 하는 방식으로 말이죠.
만약 importance 가 낮은 parameter 라면 현재 task 를 학습하는 과정에서 업데이트를 많이 하게 될 텐데요. 이는 해당 parameter 의 importance 가 다음 task 에서는 높아진다는 말이라고 할 수 있습니다.
Parameter importance 를 정의할 때 $\omega^{\mu}_{k}$ 가 사용되기 때문에, parameter importance 를 높이는 것은 곧 $\omega^{\mu}_{k}$ 값을 키우는 것과 같습니다.
Parameter 를 최적화할 때 gradient descent 방식의 최적화 기법을 사용하는 것이 일반적이므로, $\omega^{\mu}_{k}$ 값을 키우기 위해서는 마이너스 부호가 필요합니다.

Source: Section 3 - ref. [1]

실제로 $\omega^{\mu}_{k}$ 값을 계산하는 방법은, $g_k(t)$ 와 $\theta^{\prime}_k(t)$ 의 곱셈을 running sum (누적) 하는 방식으로 구현할 수 있습니다. 다만 한 가지 알아두어야 할 부분은, 우리가 딥러닝 모델을 학습시킬 때 일반적으로 stochastic gradient descent (SGD) 를 사용하여 gradient 를 계산하기 때문에, $g_k(t)$ 에 noise 가 껴있다는 사실입니다 (mini-batch 단위로 graident 를 계산하므로). 따라서 $\omega^{\mu}_{k}$ 참값보다 overestimate 되는 것이 일반적이라고 합니다.

이전 과정을 통해 $\omega^{\mu}_{k}$ 값이 무엇을 의미하는지, 어떻게 계산하는지 알게 되었습니다. 지금부터는 $\omega^{\mu}_{k}$ 값을 활용하여 catastrophic forgetting 문제를 완화하는 과정에 대해 알아보도록 하겠습니다.
목표를 다시 한 번 상기해본다면, $\boldsymbol\theta(t_2)$ 와 같이 모든 task 에 대해 준수한 성능을 보이는 parameter 를 찾는 것입니다. 다르게 말하면, 모든 task 의 loss $\mathcal{L}=\sum_{\mu}L_{\mu}$ 를 최소화하는 것이라고 얘기할 수 있겠습니다.
현재 task 인 $\mu$ 는 loss function 을 이용하여 직접적으로 최적화하는 것이 가능합니다. 다만 continual learning 에선 $\mu$ 이전 tasks 의 loss functions 에 직접적으로 접근할 수 없는 상황을 가정하고 있기 때문에, $\mathcal{L}$ 을 최소화하는 것은 생각보다 훨씬 어려운 문제입니다. Loss function 을 이용하여 task 에 대한 학습 성능을 판단하고 모델을 최적화해야 하는데, 접근할 수 없기 때문에 최적화 자체가 어려운 상황인 것이죠.
본 논문에서는 surrogate loss 라는 것을 도입하여 이전 tasks 의 loss functions 에 접근하지 못해서 발생하는 최적화의 어려움을 해결하고자 했습니다.

Surrogate loss 를 직역하면 대리 손실함수입니다. 즉 이전 tasks 의 loss functions 을 대리 (또는 근사) 하는 역할을 한다는 것이죠.

Source: figure 2 - ref. [1]

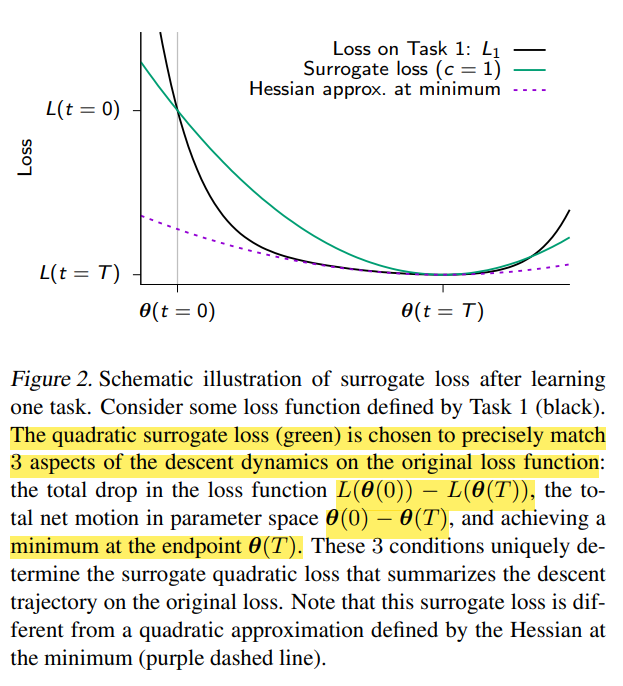
$^{1}$ 본 논문에서 정의한 surrogate loss (초록색 곡선) 는 original loss function (검은색 곡선) 이 가지는 descent dynamics (하강 방식의 최적화 과정에서 생기는 움직임) 과 3가지 측면에서 동일하기 때문에, original loss function 을 근사할 수 있다고 주장합니다.
따라서 surrogate loss 를 최적화하면, original loss function 을 최적화하는 것과 동일한 효과를 얻을 수 있다는 얘기를 하는 것이죠.

Surrogate loss 의 역할은 파악했으니, 실제로 무슨 값을 계산하고 어떻게 동작하는지 알아보도록 합시다.
본 논문에서 surrogate loss 는 지난 tasks 의 학습 과정에서 발생한 parameter trajectory 를 활용하여 parameter importance 라는 것을 정의한 뒤에, 새로운 task 를 학습할 때 importance 에 따라 parameter 의 업데이트 정도를 조절하는 방식으로 동작합니다. 쉽게 말하자면 중요한 parameter 는 가능한 그대로 두고, 중요하지 않은 parameter 만 업데이트하겠다는 것이죠.

parameter importance

Parameter importance 는 두 가지 요소를 활용하여 정의했습니다.
- 첫 번째 요소는 training trajectory 동안 task loss 가 변화하는 것에 어느 정도의 영향을 미쳤는지 나타내는 $\omega^{\nu}_{k}$ 입니다.
- 두 번째 요소는 parameter 가 얼마나 많이 이동했는지 나타내는 $\Delta^{\nu}_{k} \equiv \theta_k(t^{\nu}) - \theta_k(t^{\nu-1})$ 입니다.
$\omega^{\nu}_{k}$ 와 $\Delta^{v}_{k}$ 는 task 에서 중요한 parameter 일 수록 값이 커집니다. Task 에서 중요하다는 것은 task loss 를 최소화하는 것에 있어 중요하다는 얘기이고, task loss 를 많이 변화시킨다는 것이기에 $\omega^{\nu}_{k}$ 값 역시 커지게 됩니다. $\Delta^{v}_{k}$ 도 마찬가지로, task 에서 중요한 parameter 라면 loss 를 최소화하는 과정에서 많이 변화할 것이기에 커지게 됩니다.

parameter importance 에 따라 업데이트 정도를 조절 $\rightarrow$ regularization

이러한 특징을 활용하여 per-parameter regularization strength, 파라미터별 규제 강도인 $\Omega^{\mu}_{k}$ 를 정의하게 됩니다. 수식은 다음과 같습니다.

\tag{5} \Omega^{\mu}_{k} = \sum_{\nu<\mu} \frac{\omega^{\nu}_k}{(\Delta^{\nu}_k)^2 + \xi}

$\mu$ 는 현재 task 를, $\nu$ 는 이전 task 를 지칭하고, $\xi$ 는 분모가 0이 되는 경우를 방지하기 위해 사용하는 damping parameter 입니다.
Parameter 의 중요도가 높다면 분자와 분모 모두 커집니다. 다만 제곱으로 인해 분자보다 분모가 더 커지게 되고, 계산 결과 자체는 작아지게 됩니다.
반대로 parameter 의 중요도가 낮다면 분자와 분모 모두 작아지고, 계산 결과는 커지게 됩니다.

surrogate loss

c \sum_{k}{\Omega^{\mu}_k}(\tilde{\theta}_k - \theta_k)^2

위에서 정리한 내용을 바탕으로 정의한 surrogate loss 입니다. 기호들의 의미는 다음과 같습니다.
- $c$ : surrogate loss 의 반영 정도를 결정합니다.
- $\Omega^{\mu}_{k}$ : parameter별 규제 강도입니다.
- $\tilde{\theta}_k$ : $\theta_k(t^{\mu-1})$ 과 같은 표기로, 이전 task 학습이 끝났을 때 parameter 값을 의미합니다.
- $\theta_k$ : 현재 task 학습 과정에서 계속 변화하는 parameter 값을 의미합니다.
앞서 surrogate loss 는 중요한 parameter 는 그대로 두고, 중요하지 않은 parameter 만 업데이트하는 방식으로 동작한다고 했습니다. 실제로 그러한지 두 가지 예시를 통해 알아보겠습니다.

Importance 가 높은 parameter
- 현재 task 를 학습하는 과정에서 $\theta_k$ 값이 커졌다면, $(\tilde{\theta}_k - \theta_k)^2$ 값이 커집니다.
- $\theta_k$ 의 importance 가 높기 때문에 $\Omega^{\mu}_k$ 값은 작습니다.
- 따라서 $\Omega^{\mu}_k(\tilde{\theta}_k - \theta_k)^2$ 값이 작아지므로 gradient 값 또한 작아지게 되고, parameter 가 조금만 업데이트됩니다.
Importance 가 낮은 parameter
- 현재 task 를 학습하는 과정에서 $\theta_k$ 값이 커졌다면, $(\tilde{\theta}_k - \theta_k)^2$ 값이 커집니다.
- $\theta_k$ 의 importance 가 낮기 때문에 $\Omega^{\mu}_k$ 값은 큽니다.
- 따라서 $\Omega^{\mu}_k(\tilde{\theta}_k - \theta_k)^2$ 값이 커지므로 gradient 값 또한 커지게 되고, parameter 가 많이 업데이트됩니다.

modified loss function

이 때까지 정리한 모든 내용들을 종합해서 loss function 을 정의하게 되는데요. 수식은 아래와 같습니다.

\tag{4} \tilde{L}_{\mu} = L_{\mu} + c \sum_{k}{\Omega^{\mu}_k}(\tilde{\theta}_k - \theta_k)^2

현재 task 의 loss function 인 $L_{\mu}$ 와 지난 tasks 의 loss functions 을 대리하는 surrogate loss 를 동시에 최적화함으로써, 모든 task 에 대해 준수한 성능을 보일 수 있는 parameters 를 찾게 됩니다.

Experimental results

위에서 정의한 modified loss function 를 실험에 사용했을 때의 결과를 알아보도록 하겠습니다.

Split MNIST

Source: figure 3 - ref. [1]

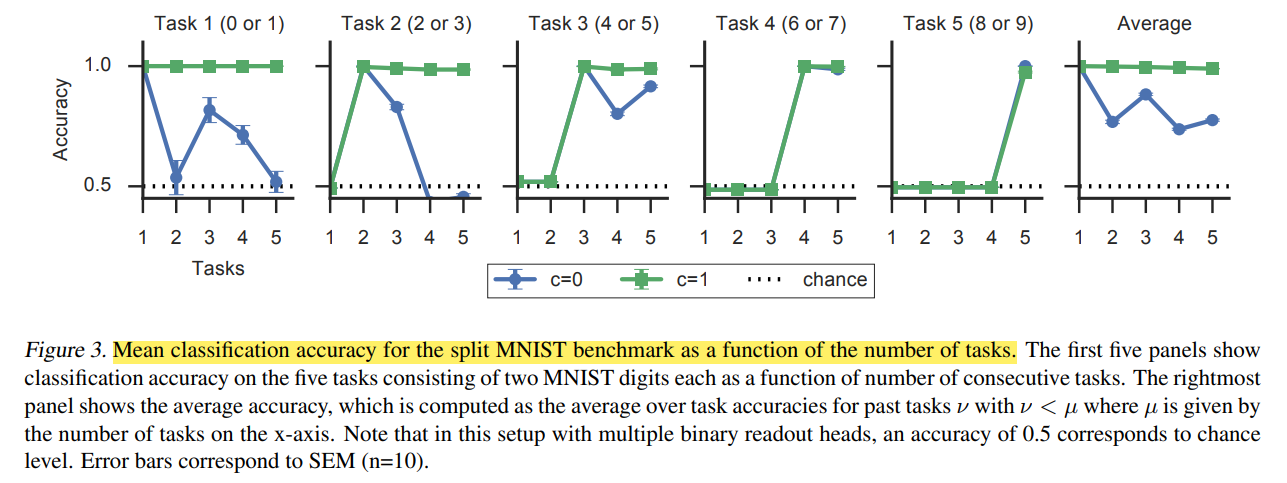
$^{2}0$ 부터 $9$ 까지 총 10가지 종류의 숫자 이미지로 구성되어있는 MNIST 데이터셋을 5개의 tasks 로 나눈 뒤, continual learning 시나리오로 학습했다고 합니다.
초록색 선은 surrogate loss 를 사용한 모델, 파란색 선은 surrogate loss 를 사용하지 않고 finetuning 한 모델입니다.
각 그래프의 점이 의미하는 것은, 해당 지점의 task 까지 학습했을 때 기준이 되는 task 의 accuracy 입니다. 즉 가장 왼쪽의 Task 1 그래프의 경우, 1번 지점은 task 1까지 학습했을 때 task 1의 accuracy 를 의미하고, 3번 지점은 task 3까지 학습했을 때 task 1의 accuracy 를 의미합니다.
일반적인 finetuing 시나리오의 경우 task 개수가 늘어남에 따라 catastrophic forgetting 이 발생하는 반면, surrogate loss 를 적용하면 지난 tasks 의 성능 또한 잘 유지한다고 주장합니다.

Permuted MNIST

Source: figure 4 - ref. [1]

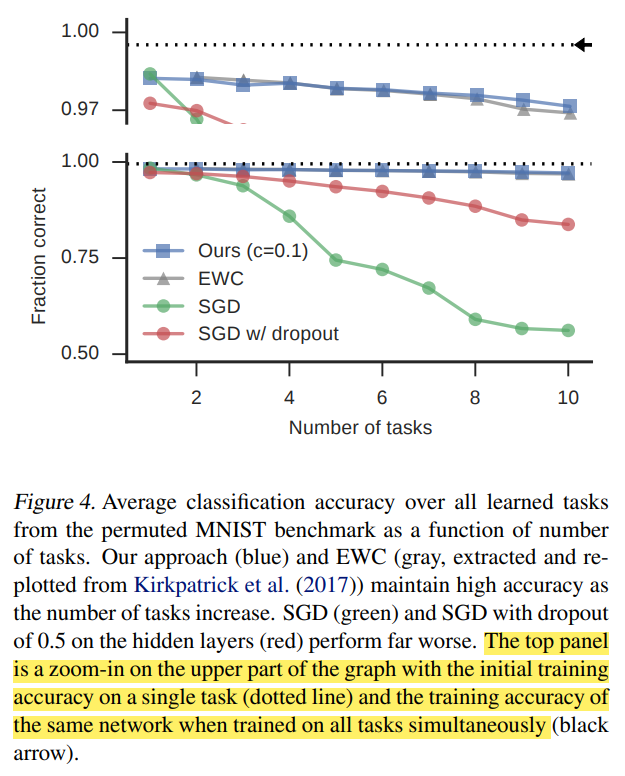
Permuted MNIST 는 기존의 MNIST 이미지를 구성하는 pixels 순서를 무작위로 바꾼 이미지 데이터셋입니다.
$^{2}$ 총 10 개의 task 가 있으며, 각각의 task 는 서로 다른 형태 (pixels 순서가 다른) 의 이미지 를 가지고 0부터 9까지 숫자 중 무엇인지 분류하는 것이 목표입니다.
일반적인 finetuning 시나리오보다 catastrophic forgetting 문제가 완화된 모습을 보이며, 또다른 regularization 기법인 EWC 와는 유사한 성능을 보이고 있습니다.

Split CIFAR-10/CIFAR-100 benchmark

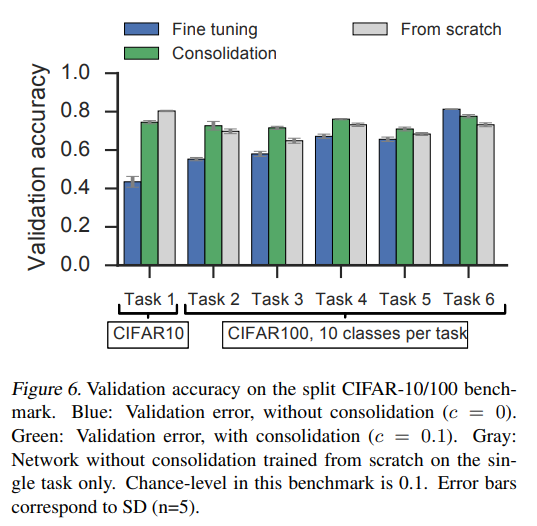
$^{2}$ Task 6 까지 모두 학습한 뒤 모델의 validation accuracy 를 나타낸 figure 입니다.
Finetuning 보다 catastrophic forgetting 문제에서 해소되었을 뿐만 아니라, single task 만 학습한 from scratch 모델과도 비슷한 성능을 보여주고 있습니다.

Summary

본 논문에서는 task 학습 과정에서 발생하는 parameter trajectory 를 이용하여 parameter importance 라는 값을 계산하고, 이 값을 기반으로 parameter 의 업데이트 정도를 조절함으로써 catastrophic forgetting 문제를 완화하고자 했습니다.
다만 continual learning 시나리오 중 task-incremental learning 에만 좋은 성능을 보이기 때문에, 풀고자 하는 문제의 성격에 따라 사용을 고민해볼 필요가 있습니다.

Reference

[1] ZENKE, Friedemann; POOLE, Ben; GANGULI, Surya. Continual learning through synaptic intelligence. In: International conference on machine learning. PMLR, 2017. p. 3987-3995.

각주

$^{1}$ 본 논문에서 제안한 surrogate loss 가 어떻게 해서 원래의 loss function 을 근사할 수 있는지에 대한 이론적인 분석은 논문의 Section 4. Theoretical analysis of special cases 에서 다루고 있습니다. 다만 해당 내용들을 이해하기 위해서는 convex optimization 에 대한 선수 지식이 필요한 관계로, 본 포스팅에서는 깊게 다루지 않았습니다.
$^{2}$ Split MNIST, permuted MNIST, split CIFAR-10/CIFAR-100 데이터셋에 대한 학습 details 은 ref. [1]의 section 5 를 참고하시길 바랍니다.

박수영

AI Engineer

다음 포스트