[Paper Review] Overcoming catastrophic forgetting in neural networks, PNAS 2017 (In Progress)

박수영·2024년 3월 27일

Continual Learning

목록 보기

2/2

시작하기에 앞서

Elastic Weight Consolidation 기법을 소개한 Overcoming catastrophic forgetting in neural networks [1] 논문을 읽고 정리한 포스팅입니다.
개인적인 해석이 일부 들어있습니다.

Background

본 논문은 신경 과학 (neuroscience) 의 synaptic consolidation 현상으로부터 영감을 받아 연구를 진행했습니다.
Synaptic consolidation 이란, 새로운 것을 학습하는 과정에서 활성화된 synapse 의 상태를 오랫동안 유지하는 것을 의미합니다. 쉽게 말해 공부한 내용을 까먹지 않는 것이라고 얘기할 수 있겠습니다.
공부한 내용을 까먹지 않을 수 있는 이유로는, 아마도 과거의 데이터를 학습하는 과정에서 활성화된 synapse 의 상태를 유지할 수 있는 능력이 있기 때문일 것입니다.
Synapse 의 상태를 유지한다는 것은, 다시 말해 새로운 데이터를 학습하는 과정에서 이전에 활성화된 synapse 의 상태가 변화하지 않도록 제어한다는 것입니다. 신경과학에서는 plasticity 를 줄인다고 얘기합니다.
본 논문에서 제안한 EWC 알고리즘은 이러한 신경과학적 사실을 알고리즘으로 구현함으로써 파괴적 망각 (catastrophic forgetting) 현상을 완화하고자 했습니다.

Elastic Weight Consolidation (EWC)

Source: figure 1 - ref. [1]

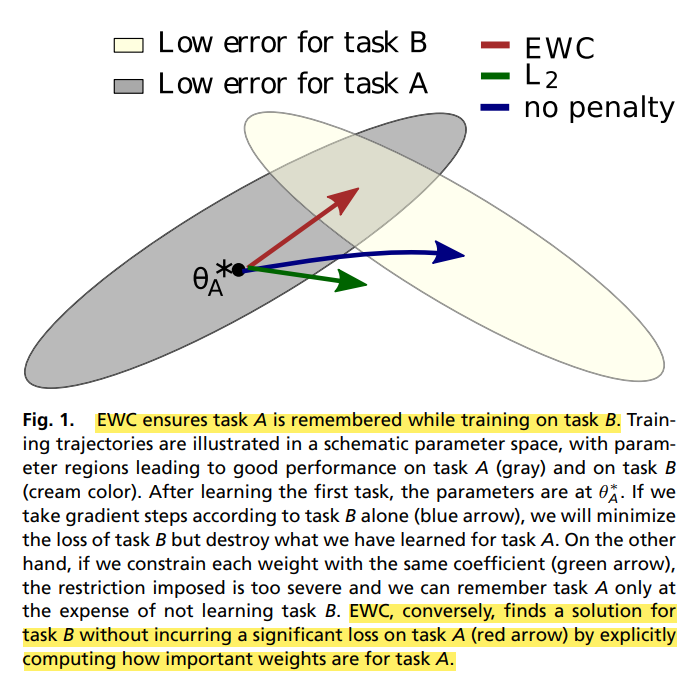
Figure. 1. 은 EWC 알고리즘의 동작 방식을 잘 설명해주고 있습니다.
회색 타원은 task A 에 대해 낮은 error 를 기록한 파라미터 공간을 의미하고, 아이보리색 타원은 task B 에 대해 낮은 error 를 기록한 파라미터 공간을 의미합니다.
Task A 에 대한 학습을 마쳤을 때 파라미터는 ${\theta_{A}}^{\ast}$ 에 위치합니다. 그 상태에서 아무런 페널티를 적용하지 않고 task B 를 학습한다면, 파라미터는 아이보리색 타원 영역으로 이동할 것입니다. 이러한 경우 task B 에 대해서는 낮은 error 를 기록하겠지만, task A 에 대해서는 높은 error 를 기록하게 됩니다. 쉽게 말해 task A 에 대해 학습한 지식을 대부분 까먹게 되는 것이죠.

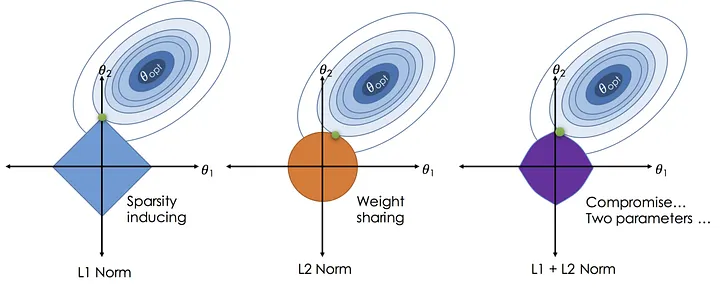
L2 regularization 과 같은 기법을 적용한다면 어떨까요? L2 regularization 은 학습하고자 하는 task 의 loss function 을 최적화하는 것과 더불어, 파라미터가 너무 커지는 것을 방지하는 방향으로 최적화를 수행합니다. 수식은 아래와 같습니다. (수식의 뒷 부분이 L2 regularization 입니다)

L_{total} = L_{task}(\bold{Y}, \bold{\hat{Y}}) + \frac{\lambda}{2}{|\bold{W}|^2}

Source: The Art of Regularization, Aishwarya Nair

L2 regularization 은 파라미터에 대한 제한을 걸어줌으로써 모델의 overfitting 문제를 완화합니다. (제한 정도는 $\lambda$ 를 통해 조절합니다) 다만 파라미터가 가지는 의미는 전혀 고려하지 않기 때문에, continual learning 시나리오에는 적합하지 않습니다. Figure. 1. 에서 초록색 선을 보시면, task B 를 학습했음에도 task A 와 B 모두에 대한 성능이 애매한 것을 알 수 있습니다.

반면에 EWC 알고리즘은 task A 에 대해 낮은 error 를 기록한 파라미터 공간을 크게 벗어나지 않으면서도, task B 에 대해 낮은 error 를 기록하는 파라미터 공간을 찾을 수 있다고 주장합니다. 어떻게 가능한 걸까요?

Source: Results - ref. [1]

본 논문에서는 EWC 알고리즘이 동작하는 원리를 크게 세 가지 흐름으로 설명합니다.
가장 먼저, 새로운 task 에 적합한 파라미터를 과거에 학습한 파라미터 위치의 근처에서 찾는 이유를 설명합니다. 그 다음으로 이전 task 에서 학습한 파라미터의 정보를 유지하는 것과 동시에, 새로운 task 에 적합한 파라미터를 찾기 위해 제한을 거는 방법을 설명합니다. 마지막으로 특정 task 에서 어떤 파라미터가 중요한 지 정의하는 방법에 대해 설명합니다.

새로운 task 에 적합한 파라미터를, 과거에 학습한 파라미터 위치의 근처에서 찾는 이유

생각보다 단순합니다. 딥러닝 모델을 학습하다 보면, 서로 다른 파라미터 구성임에도 불구하고 동일한 성능을 보이는 경우가 많습니다. 이러한 실험적 사실을 기반으로, 특정 task 에 대해 동일한 성능을 보이는 파라미터 공간 (parameter space) 이 존재할 수 있다는 것을 유추할 수 있습니다.
파라미터 공간에 얼마나 많은, 서로 다른 파라미터가 존재할 지는 알 수 없지만, 모델 아키텍처가 충분히 크다고 가정한다면 수많은 파라미터가 존재할 것입니다. 파라미터 공간 내에 존재하는 수많은 파라미터 중에, 현재 task 뿐만 아니라 미래에 학습할 task 에도 적합한 파라미터가 존재할 확률이 높다고 가정할 수 있습니다. EWC 알고리즘은 이 가정을 기반으로 시작되었습니다.

이전 task 에서 학습한 파라미터의 정보를 유지하는 것과 동시에, 새로운 task 에 적합한 파라미터를 찾기 위해 제한을 거는 방법 && 특정 task 에서 어떤 파라미터가 중요한 지 정의하는 방법

사실 새로운 task 에 적합한 파라미터를, 과거에 학습한 파라미터 위치의 근처에서 찾는 것은 그리 중요한 내용이 아닙니다. 그보다 중요한 것은 과거의 정보를 유지한 채로 새로운 정보를 학습하는 부분이죠.
새로운 정보를 학습한다는 말은, 딥러닝 분야에선 새로운 데이터를 학습한다는 말과 같습니다. 새로운 데이터를 학습한다는 것은, 데이터에 맞게 모델을 구성하는 파라미터들을 최적화한다는 얘기입니다. 모델을 구성하는 파라미터는 가변적이지 않고, 고정적입니다. 쉽게 말해 학습 과정에서 파라미터의 개수를 키우거나 줄일 수 없다는 얘기이죠.
학습할 수 있는 파라미터의 개수가 고정된 상태에서, 이전에 학습한 정보를 유지한 채로 새로운 정보를 학습하려면 어떻게 할 수 있을까요? 본 논문에서는 task 학습 과정에서 어떤 파라미터가 중요한 지 정의하고, 중요한 파라미터들이 변화하는 것을 제한하는 방식으로 이 작업을 수행합니다.
예를 들어, task A 에 대한 학습을 마쳤을 때 파라미터의 값이 $\bold{\theta} = \begin{bmatrix}1&2&3\end{bmatrix}$ 인 상황이라고 생각해봅시다. 어떠한 방법을 통해 $\bold{\theta}_{1} = 2$ 가 task A 에서 중요하다고 정의했습니다. 이후 새로운 task B 를 학습할 때, EWC 는 $\bold{\theta}_{1} = 2$ 가 변화하는 것을 제어하고, $\bold{\theta}_{1}$ 과 $\bold{\theta}_{3}$ 을 업데이트하는 방향으로 학습을 진행합니다.

\tag{1} \mathcal{L}(\theta) = \mathcal{L}_B(\theta) + \sum_{i}{\frac{\lambda}{2} F_i (\theta_i - \theta^{\ast}_{A,i})^2}

수식 (1)은 EWC 알고리즘을 적용한 최종 손실 함수를 나타냅니다. 오른쪽 변에서 $\mathcal{L}_B(\theta)$ 를 제외한 나머지 부분이 EWC 알고리즘입니다.
Task A 를 학습한 후, task B 를 학습하는 과정에서 사용하는 손실 함수입니다. Task A 를 학습할 때에는 EWC 알고리즘이 필요하지 않습니다.
$\mathcal{L}_B(\theta)$ 는 task B 에 대한 손실 함수를 의미하고, $\lambda$ 는 과거에 학습한 정보를 어느 정도로 기억할 것인지 조정하는 역할을 합니다. $F$ 는 fisher information matrix 를 의미하고, $i$ 는 $i$ 번째 파라미터를 나타냅니다. ${\theta_{A}}^{\ast}$ 는 task A 학습을 마쳤을 때 파라미터 값을 의미합니다.
수식은 간단한 편이지만, 이를 이해하기 위해서는 다양한 사전 지식이 필요합니다. 해당 내용들은 아래 Details 에서 다루어보도록 하겠습니다.

EWC: Details

EWC: Details 파트를 통해 알고자 하는 것은 다음과 같습니다.
1. 특정 task 에서 어떤 파라미터가 중요한지 정의하는 방법과 근거
2. 중요한 파라미터에 제한 (constraints) 을 적용하는 방법과 근거
3. EWC 알고리즘의 구현 방법
위 세 가지 항목을 순서대로 정리해보도록 하겠습니다.

특정 task 에서 어떤 파라미터가 중요한지 정의하는 방법과 근거

신경망의 학습을 다른 관점에서 해석하기

'딥러닝' 하면 일반적으로 떠오르는 생각은, 적절한 손실 함수와 경사하강법 기반의 최적화 알고리즘을 사용하여 신경망을 이루는 파라미터들 (weight, bias) 을 최적화하는 것입니다.
여기서 신경망 에 대해 좀 더 생각해봅시다. 일반적으로 딥러닝에서 모델 이라고 말하는 신경망은, 하나의 함수로 생각할 수 있습니다. 함수라고 함은, 임의의 입력 $x$ 가 주어졌을 때 $y$ 를 출력하는 일종의 규칙입니다. 딥러닝에서 $x$ 는 데이터이고, $y$ 는 우리가 풀고자 하는 문제의 정답입니다. 예를 들어 주어진 이미지가 개인지 고양이인지 분류하는 딥러닝 모델을 만들고자 한다면, $x$ 는 이미지이고 $y$ 는 개 또는 고양이가 되겠죠.
즉 데이터가 주어졌을 때 그에 맞는 정답을 출력하는 함수를 찾는 것이 딥러닝의 목표인 것입니다.
이러한 함수를 찾는 방법은 여러 가지가 있는데, 그 중에서 가장 대중적으로 사용하는 방법이 손실 함수 + 경사하강법 기반의 최적화 방법입니다. 그 다음으로 유명한 방법이 있다면, 최대 우도 추정 (Maximum Likelihood Estimation, 이하 MLE) 방법이 있겠네요.
EWC 알고리즘의 디테일을 이해하기 위해선, 신경망의 학습 과정을 MLE 로 해석할 수 있어야 합니다. (해석이라고 말하는 이유는, 신경망을 바라보는 관점이 다를 뿐 학습 과정은 거의 유사하기 때문입니다) 따라서 MLE 가 무엇인지, 차근차근 정리해보도록 하겠습니다.

우도, 가능도(Likelihood)

다음으로 알아야 할 것은 likelihood 에 대한 개념입니다.

The likelihood function (often simply called the likelihood) is the joint probability mass (or probability density) of observed data viewed as a function of the parameters of a statistical model. Intuitively, the likelihood function $\mathcal{L}(\theta|x)$ is the probability of observing data $x$ assuming $\theta$ is the actual parameter. - likelihood, wikepedia

일반적으로 likelihood 라고 부르는, likelihood function 은 통계학적 모델의 특성을 결정하는 parameters 에 대한 함수입니다. 더 쉽게 얘기하자면, 입력으로 parameter 가 주어지면 likelihood 를 출력하는 함수를 말합니다.
통계학에서 parameter 는 어떤 확률 분포의 형태와 성질을 결정짓는 모수를 말합니다. 가우시안 분포와 같은 확률 분포의 parameter 는 평균( $\mu$ )과 분산( $\sigma$ )이 있죠. 이러한 parameter 값이 입력으로 주어지면 어떤 분포의 형태와 성질을 결정지을 수 있고, 이를 바탕으로 likelihood 를 계산하게 되는 것입니다.
그런데 왜 probability function 이라고 말하지 않고 굳이 likelihood function 이라고 부르는 걸까요?
Probability 와 likelihood 는 서로 다른 개념이기 때문입니다. 전통적인 통계학 관점에서 probability 는 확률 분포를 명확하게 알아야만 계산할 수 있습니다. 이와 반대로 likelihood 는 확률 분포를 명확하게 알 수 없는 상태에서 계산하는 것이므로, probability 라고 부르지 않고 likelihood 라고 부르는 것입니다. "실제 정확한 확률 분포는 모르겠지만 만약 parameter 가 이러한 값이라면 그 때의 확률은 아마도 이런 값일거야. 다만 확률 분포를 정확히 아는 상태에서 계산한 게 아니니깐, 가능할 수 있는 값이라고 해서 가능도, 또는 우도라고 정의하자." 같은 느낌입니다.

베이즈 정리(Bayes' theorem)

P(A|B) = \frac{P(B|A)P(A)}{P(B)}

베이즈 정리의 수식은 위와 같습니다만, 베이즈 정리가 가지고 있는 의미를 더 잘 이해하기 위해 아래와 같이 표기를 조금 바꿔보겠습니다.

\tag{2} P(H|E) = \frac{P(E|H)P(H)}{P(H)P(E|H) + P(\neg{H})P(E|\neg{H})} = \frac{P(E|H)P(H)}{P(E)}

Reference

[1] KIRKPATRICK, James, et al. Overcoming catastrophic forgetting in neural networks. Proceedings of the national academy of sciences, 2017, 114.13: 3521-3526.
[2] AICH, Abhishek. Elastic weight consolidation (EWC): Nuts and bolts. arXiv preprint arXiv:2105.04093, 2021.

박수영

AI Engineer

이전 포스트