[논문 발표]Efficient Estimation of Word Representations in Vector Space

numver_se·2021년 3월 17일

💡 논문 발표

Efficient Estimation of Word Representations in Vector Space

위 그림처럼 동물들이 있다고 할 때, 컴퓨터는 이를 이해할 수 없습니다. 컴퓨터가 이해할 수 있게 하기 위해서는 이 동물들이 수치적인 방식으로 표현되어야 합니다. 이러한 문제는 언어에도 똑같이 적용되는데요. 그러면 어떻게 수치적인 방식으로 표현할 수 있을까요?

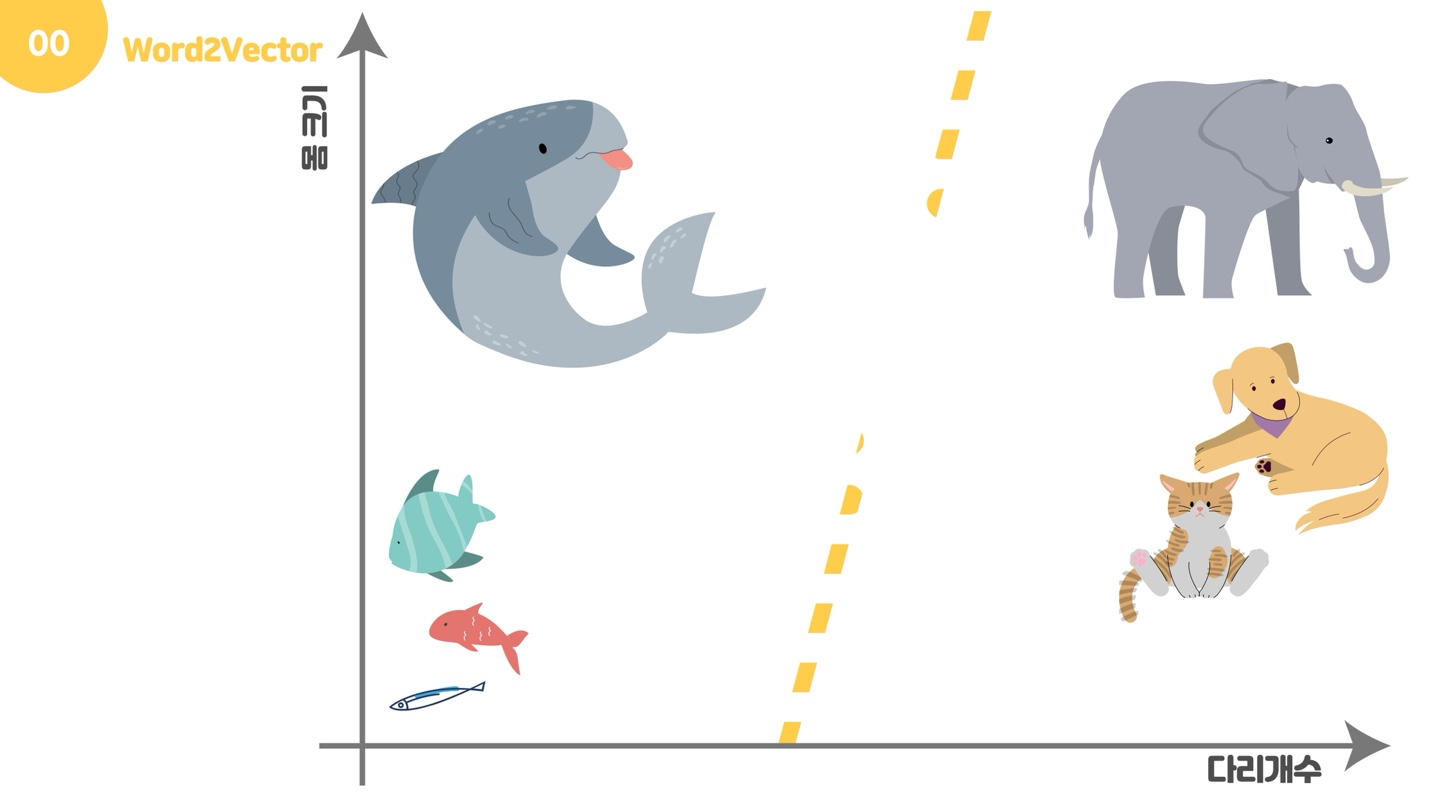
이 그래프처럼, 어떠한 기준을 가지고 좌표평면에 표현한다면 우리는 동물들을 수치화하여 표현할 수 있습니다. 그러면 우리가 궁금한 언어에 이를 적용시킬 때, 무엇을 기준으로 하여 좌표평면으로 표현할 수 있을까요?

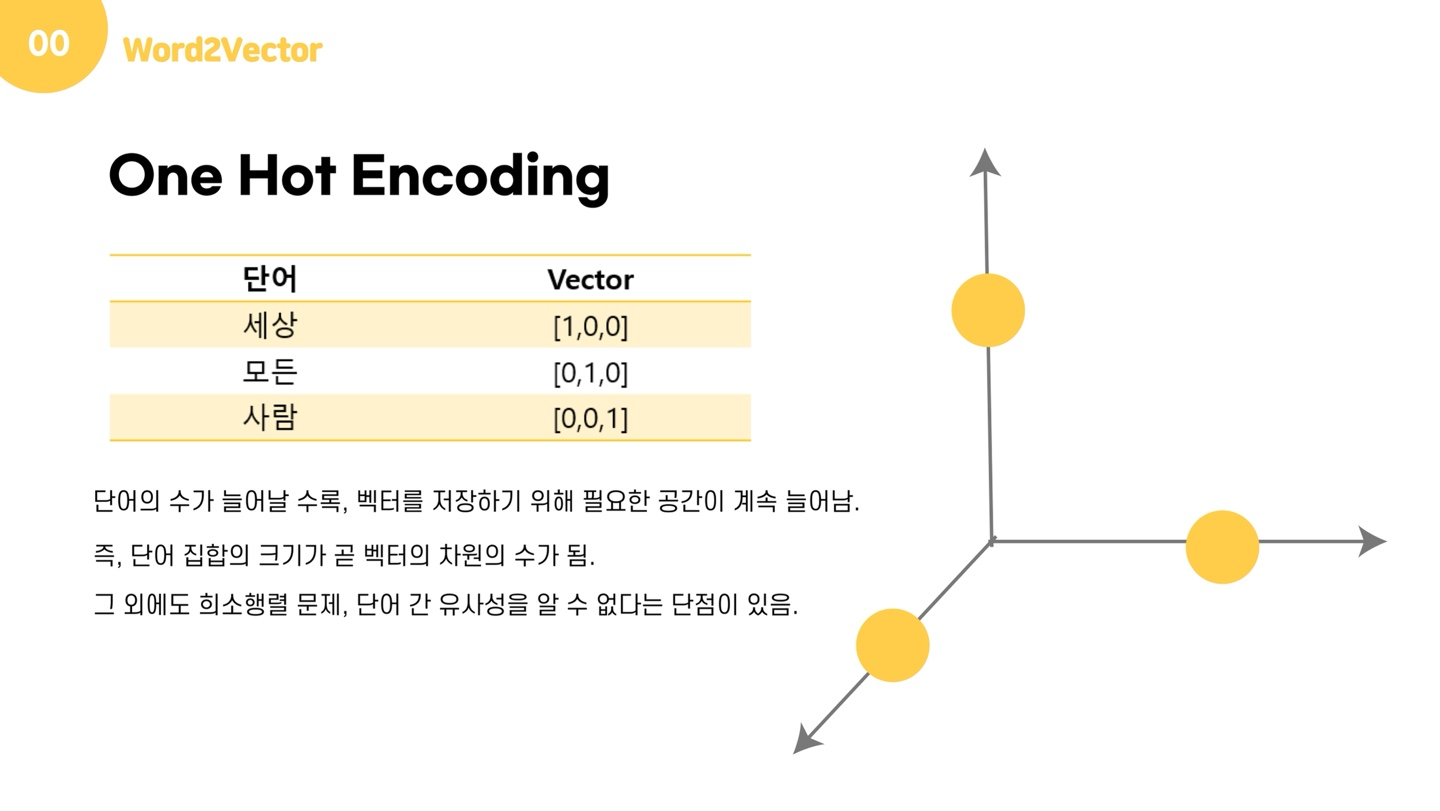
가장 간단한 방법은 one-hot encoding일 것입니다. '세상, 모든, 사람'으로 이루어진 사전(Dictionary)가 있다고 가정해보겠습니다. 이때 우리는 길이 3짜리 벡터를 만들고, 그 단어가 해당되는 자리에 1을 넣고 나머지 자리들에 0을 넣어 단어를 표현할 수 있습니다. 지금은 단어가 3개밖에 없기 때문에 그래프로 나타내도 알아볼 수 있는 형태지만, 단어가 십만개가 주어진다고 생각해봅시다. 단어가 십만개라면, 벡터의 차원도 십만개가 됩니다. 즉, n개의 단어를 표현하기 위해서는 n차원의 벡터가 필요한 것이죠.

차원수가 높으면 훈련 데이터를 많이 필요로 하게 되는데다가, 메모리 사용이 늘어나고, 계산 복잡도가 매우 늘어나게 되는 '차원의 저주'에 빠질 수 있습니다. 또한, 단 하나의 값만 1을 가지고 9만 9999개의 값은 0을 가지는 희소행렬 문제를 갖게 되기에, 저장 공간 측면에서도 매우 비효율적인 방법입니다. one-hot encoding은 각각이 독립적인 축을 가지고 있기에 단어 간 유사성을 알 수 없는데, 현실에서는 단어들이 서로 의미적인 관계를 갖고 있습니다. 이러한 문제들을 해결하기 위해 등장한 개념이 바로 Distributed Representation이며, 앞으로 이를 분산표현이라고 부르겠습니다.

분산표현은 기본적으로 distributional hypothesis라는 가정 하에서 나온 방법입니다.

💡 distributional hypothesis
A word's meaning is give by the words that frequently appear close-by(비슷한 위치에서 자주 등장하는 단어들은 비슷한 의미를 가진다)

예를 들어, 강아지라는 단어는 귀엽다, 사랑스럽다, 예쁘다 등의 단어와 함께 등장하는 경우가 잦기 때문에, distributional hypothesis에 따라서 저 단어들은 의미적으로 가까운 단어가 됩니다.

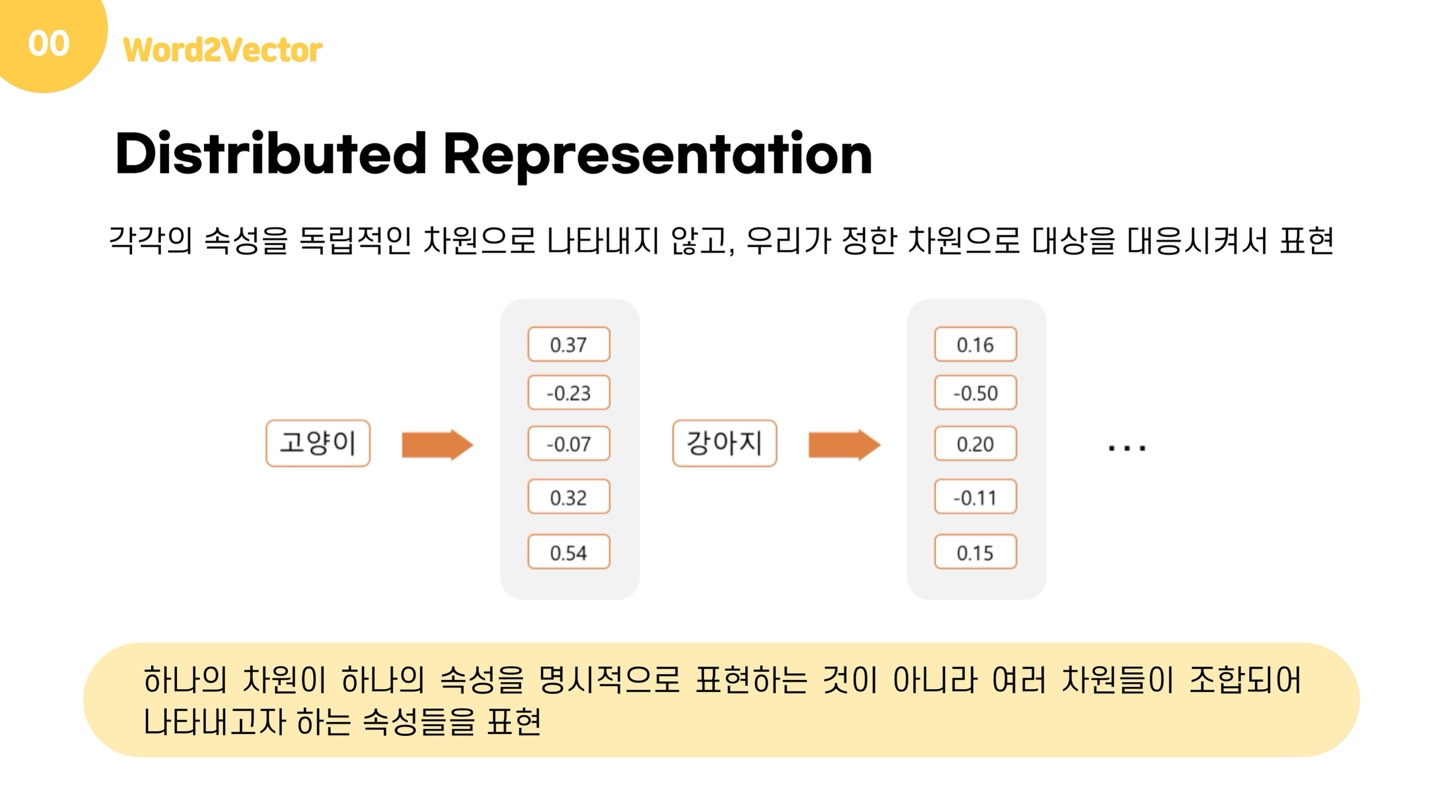
분산표현은 이 가설에 따라 단어들을 학습하고, 벡터에 단어의 의미를 여러 차원에 분산하여 표현합니다. 다시말해, one-hot encoding은 각각의 속성을 독립적인 차원에 나타냈던 것과 다르게 분산 표현은 우리가 정한 차원(여기서는 차원이 5입니다)에 대응하여 표시됩니다. 그림에서 볼 수 있듯이 대상을 대응시켜 여러 차원에 분산하여 표현한다는 것입니다. 아까의 원핫인코딩 처럼 하나의 차원이 하나의 속성을 명시적으로 표현하는 것이 아니라, 여러 차원들이 조합되어 나타내고자 하는 속성들을 표현하는 것을 확인할 수 있습니다.

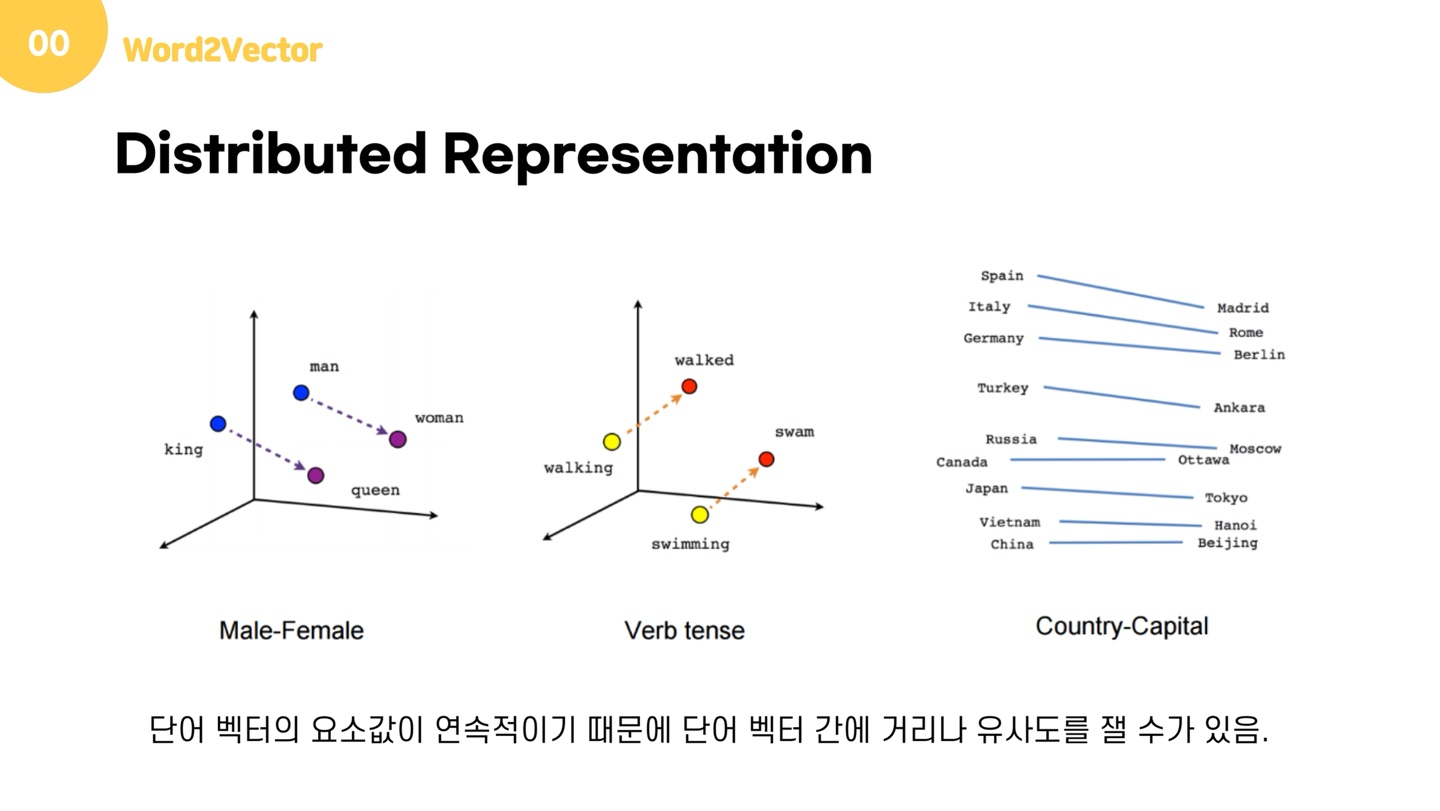
분산표현을 사용하면 1) 데이터의 차원 수를 줄일 수 있습니다. 또한, 단어의 의미 자체를 벡터화할 수 있게 되었기 때문에, 2) 단어의 유사도를 계산할 수 있습니다. 또한 3) 벡터 연산이 가능해지기 때문에 이를 통해 단어 추론이 가능해진다는 점도 큰 장점입니다.

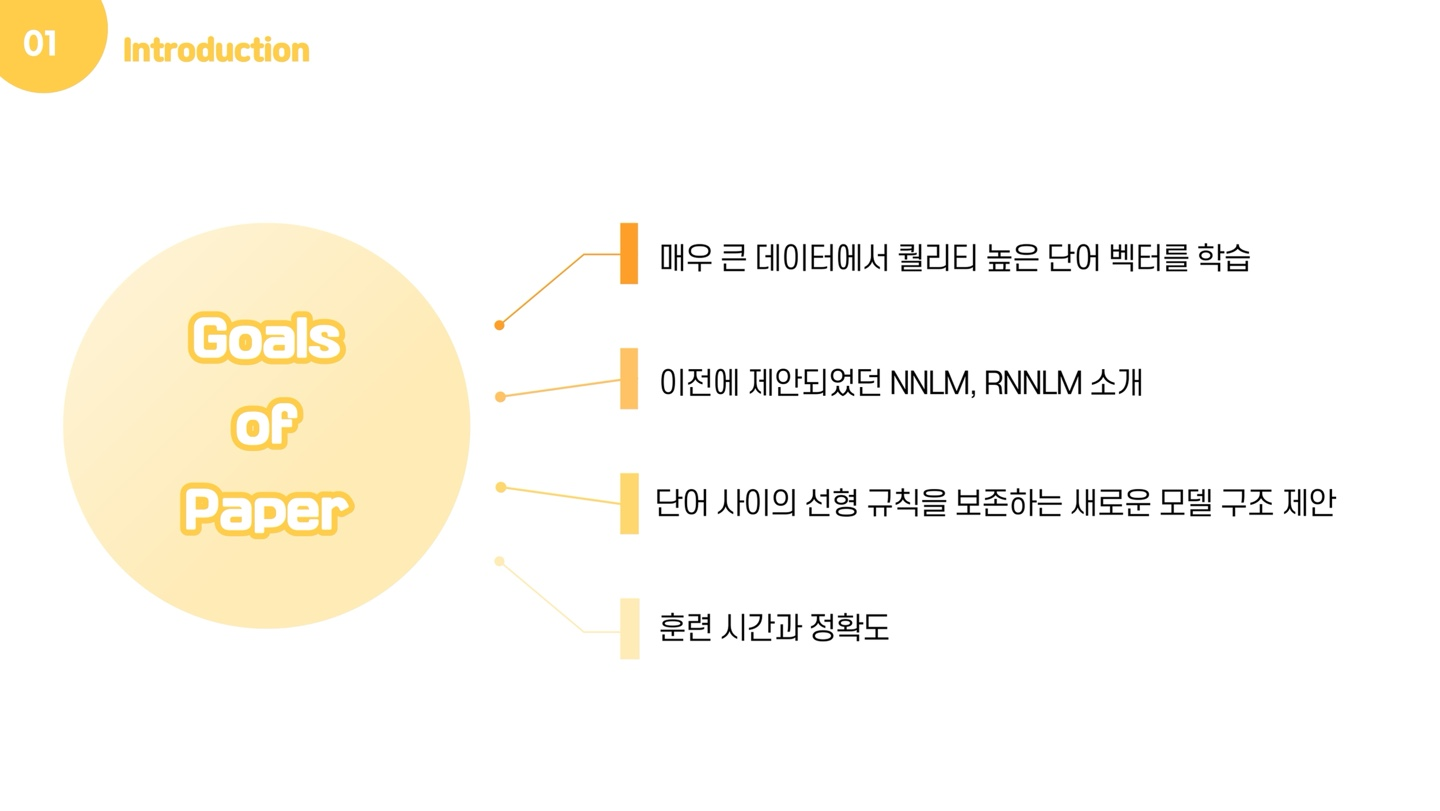
그렇다면 이제는 '어떻게 각 단어를 벡터화해야 하는가' 가 화두가 될 것입니다. 사실 단어를 벡터화하는 방법 자체는 예전부터 이야기되어왔던 문제입니다. 따라서 본 논문에서는 먼저, 매우 큰 데이터에서 퀄리티 높은 단어 벡터를 학습할 수 있는 기술들로 이야기 되어 왔던 NNLM, RNNLM 에 대해 소개합니다. 그 후, 본 논문에서 제안하는 모델 구조인 CBOW와 Skip-gram을 소개하고, 마지막으로 훈련 시간과 정확도가 단어 벡터의 차원과 training 데이터의 양에 얼마나 의존하는지 설명합니다.

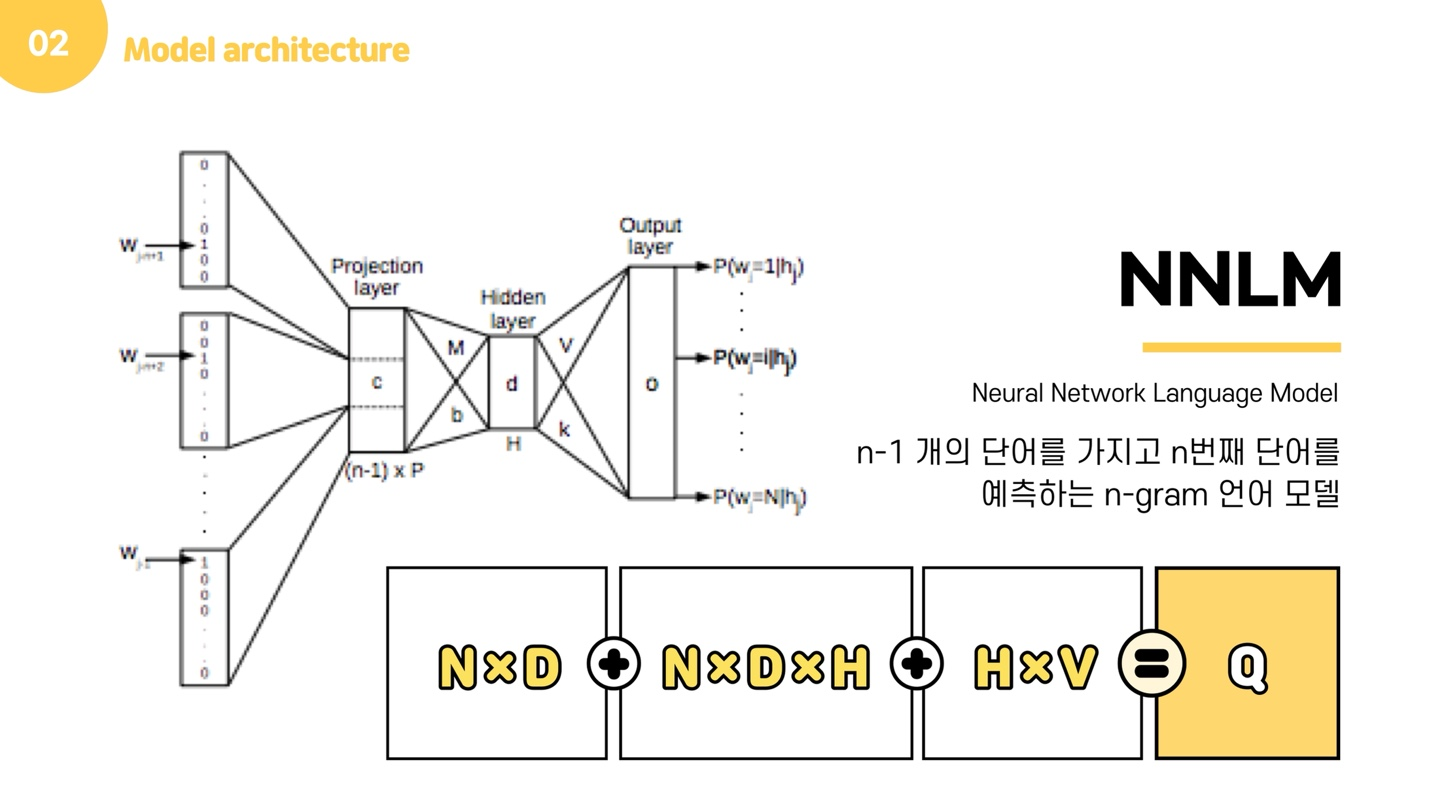
그러면 본격적으로 모델 구조에 대해 설명드리겠습니다. 본 논문에서 가장 먼저 소개하는 모델은 NNLM입니다. NNLM은 n-1 개의 단어를 가지고 n번째 단어를 예측하는 n-gram 언어 모델입니다. 즉, 어휘 집합이 주어지고 다음 단어가 무엇인지 맞추는 과정에서 학습을 합니다. NNLM은 Input layer, Projection layer, Output later로 이루어진 신경망 구조를 가지고 있습니다.

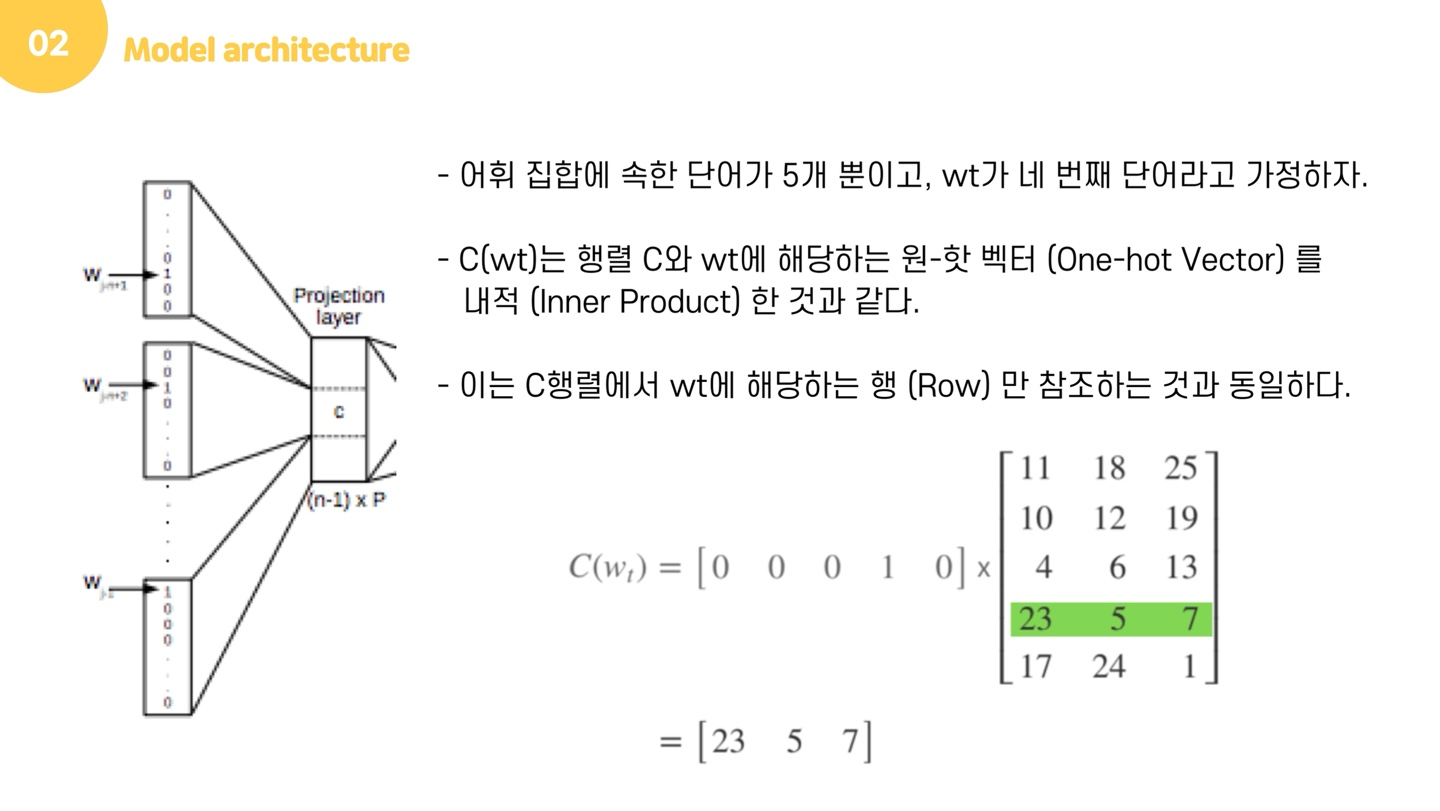
보다 모델 구조를 알기 쉽게 설명하기 위해, 어휘 집합에 속한 단어가 5개라고 합시다. 우리는 window size=4로 설정하여, 4개의 단어를 가지고 마지막 단어를 예측할 것입니다. 이 때, 어휘집합은 ['나는', '귀여운', '강아지를', '정말', '좋아해']라고 하겠습니다. $W_t$ 가 네번째 단어라고 하면, $W_t$ 는 '정말'이 될 것입니다. Input layer에서 정말은 one-hot vector로 바뀌어 [0,0,0,1,0]으로 입력됩니다. 이 때, projection layer에서는 행렬 $C$ 를 만듭니다. $C$ 행렬의 크기는 $N$ (단어의 수) x $D$ (projection layer의 크기)이며, 행렬의 초기 값은 랜덤으로 초기화 됩니다. 즉, 단어의 수는 5이고, projection layer의 크기는 3이기 때문에 5x3의 크기인 행렬 $C$ 가 $W_t$ ([0,0,0,1,0])에곱해집니다. 이 때, one-hot vector의 특성 때문에 $W_t$ 와 $C$ 의 곱은 사실 $C$ 행렬의 $t$ 번째 행을 그대로 참조해오는 것과 같습니다. 이 참조작업을 거치면 one-hot vector의 차원수는 5에서 3으로 줄어들게 됩니다. 이 벡터들은 초기에 랜덤한 값([23, 5, 7])을 가지지만 학습과정에서 값이 계속 변경됩니다. 이렇게 학습된 벡터는 output layer에서 softmax 함수가 적용되어, 각 원소는 0과 1 사이의 실수값을 가지며 총합이 1이 되는 상태로 바뀝니다.

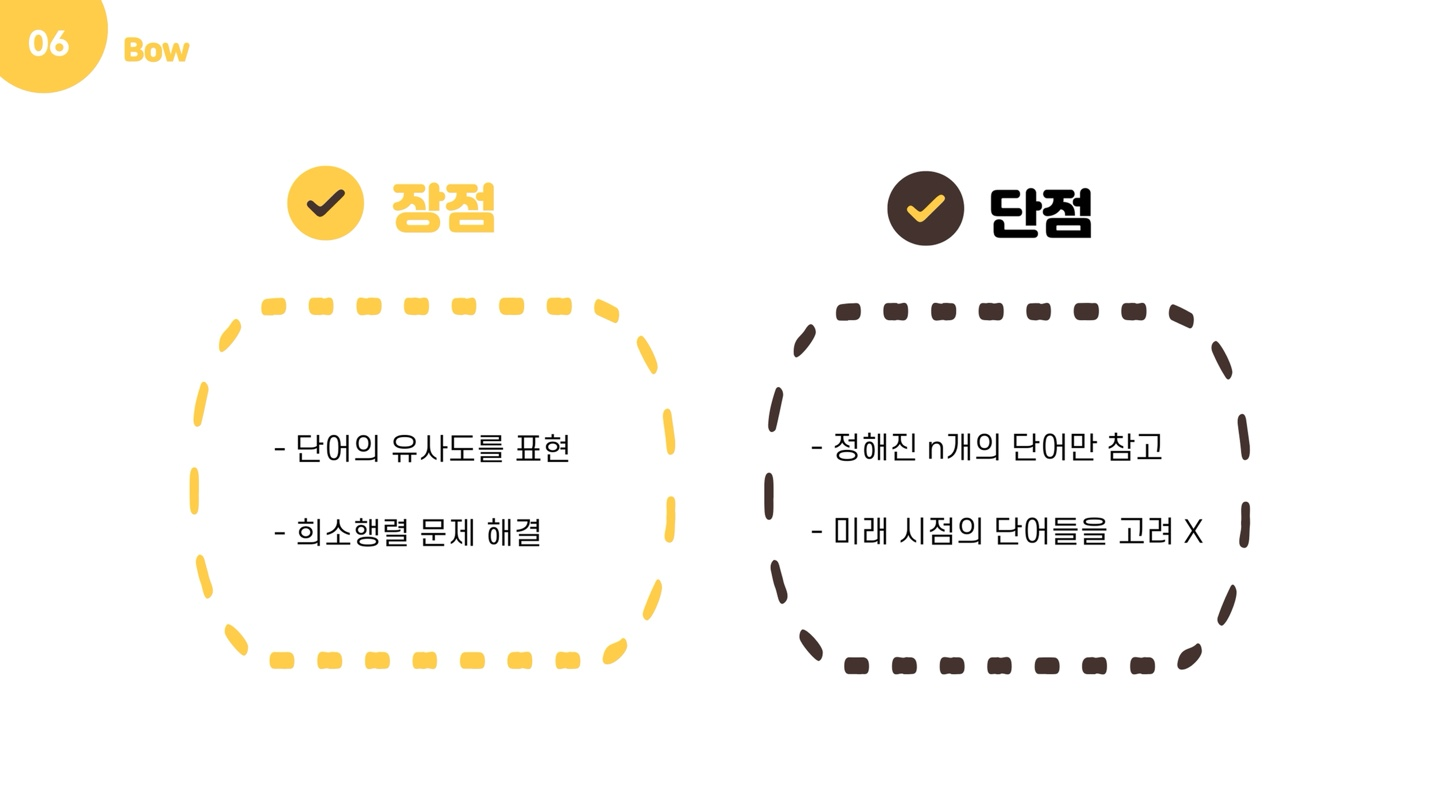
NNLM은 단어의 유사도를 표현할 수 있으며, 희소행렬 문제가 해결되는 장점을 가집니다. 그러나 고정된 개수의 단어만을 입력받을 수 있으며, 미래 시점의 단어들을 고려하지 않는다는 단점을 가지고 있습니다.

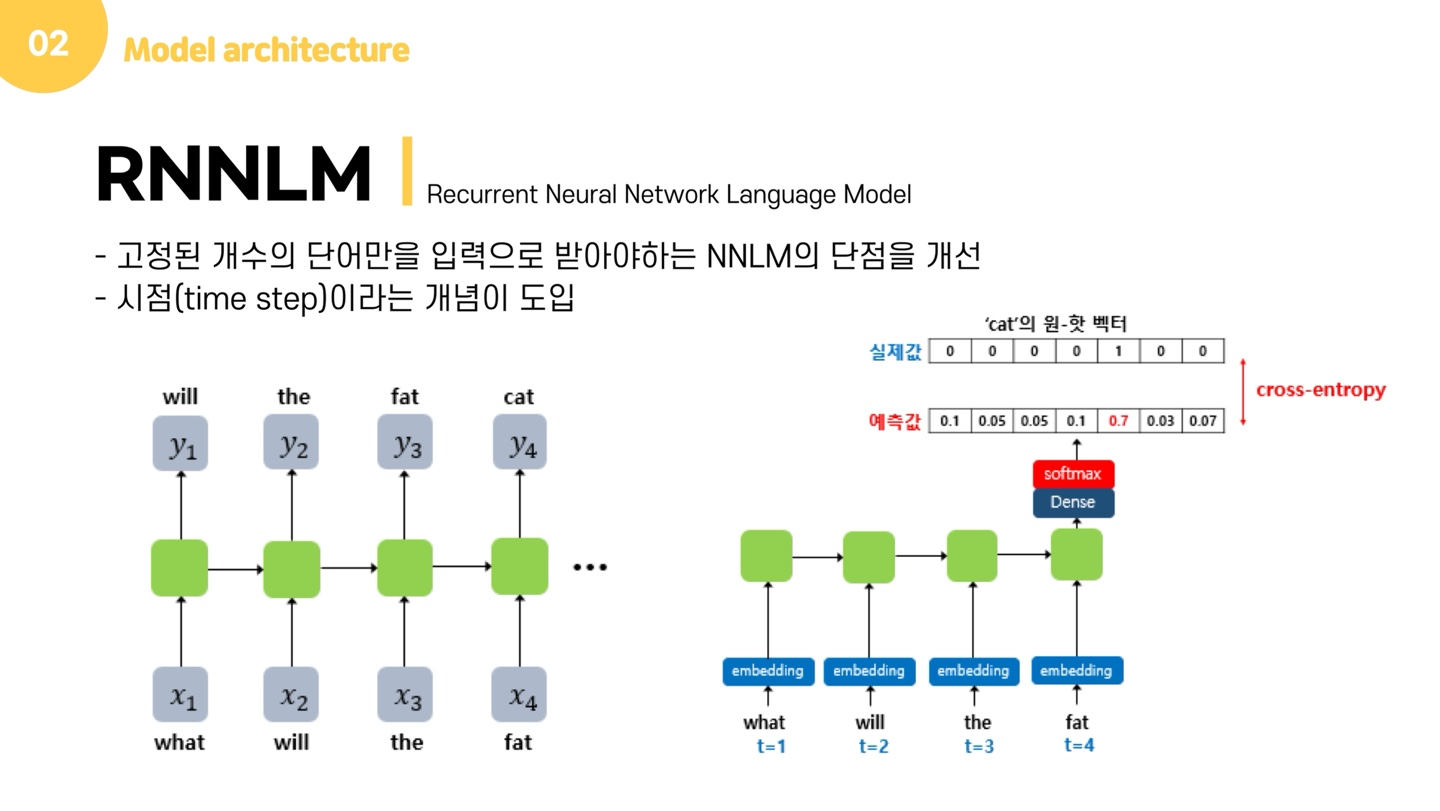
이러한 문제를 해결하기 위해 도입된 모델이 바로 RNNLM입니다. RNNLM은 시점이라는 개념이 도입되어, 입력의 길이를 고정하지 않고 학습할 수 있어 기존의 문제가 해결됩니다. RNNLM은 기본적으로 예측 과정에서 이전 시점의 출력을 현재 시점의 입력으로 합니다. 예를 들어, "what will the fat cat sit on"이라는 문장이 있을 때, RNNLM은 what을 입력받으면, will을 예측하고 이 will은 다음 시점의 입력이 되어 the를 예측합니다.

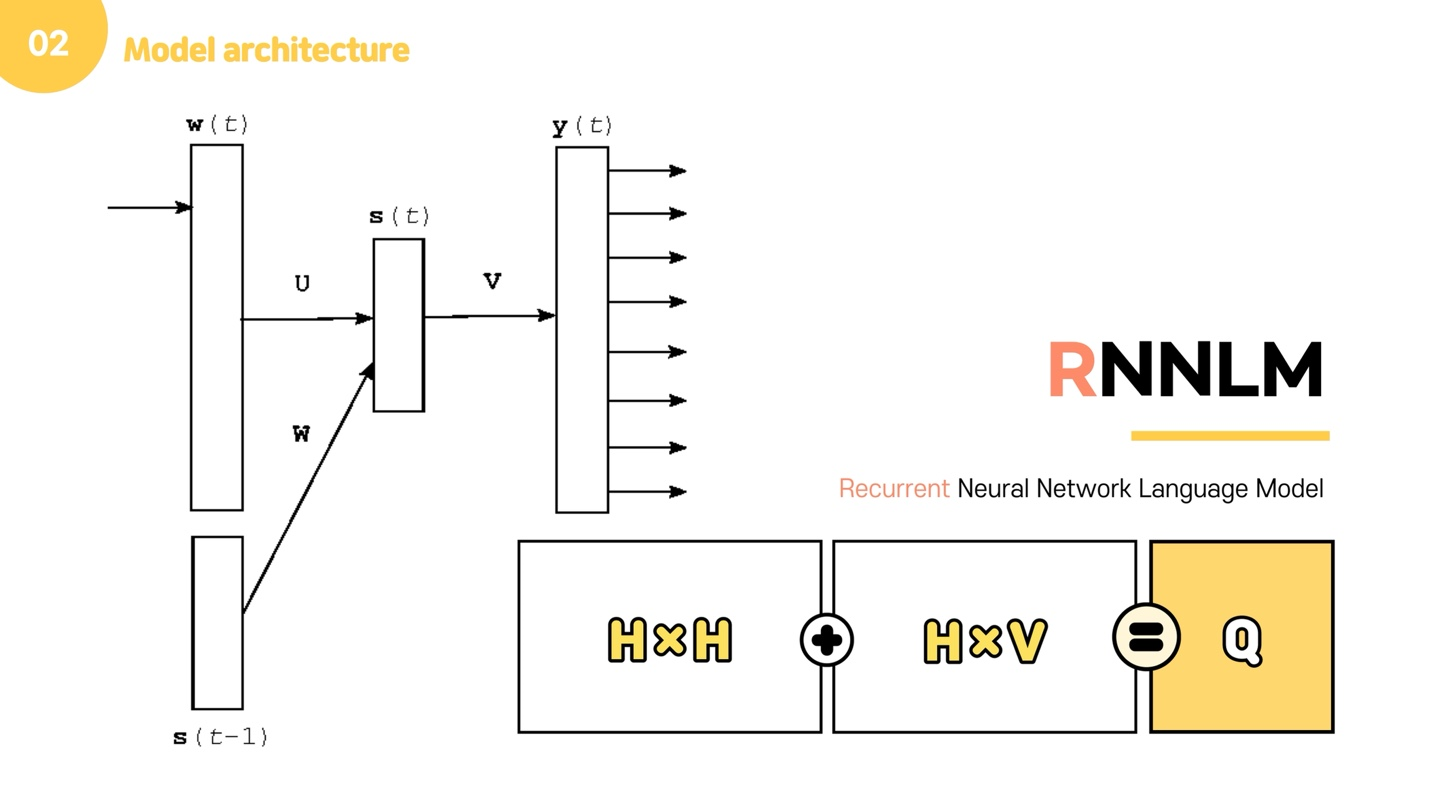
그런데 저는 이 모델 그림을 보고 의문이 들었는데, 어떤 그림에는 되풀이 화살표가 있기도 하더라구요. 그런데 제가 들고온 이 그림에는 화살표가 없어서 이에 대해 찾아보니 아마도 'teacher forcing' 때문인 것 같다는 결론을 내렸습니다.

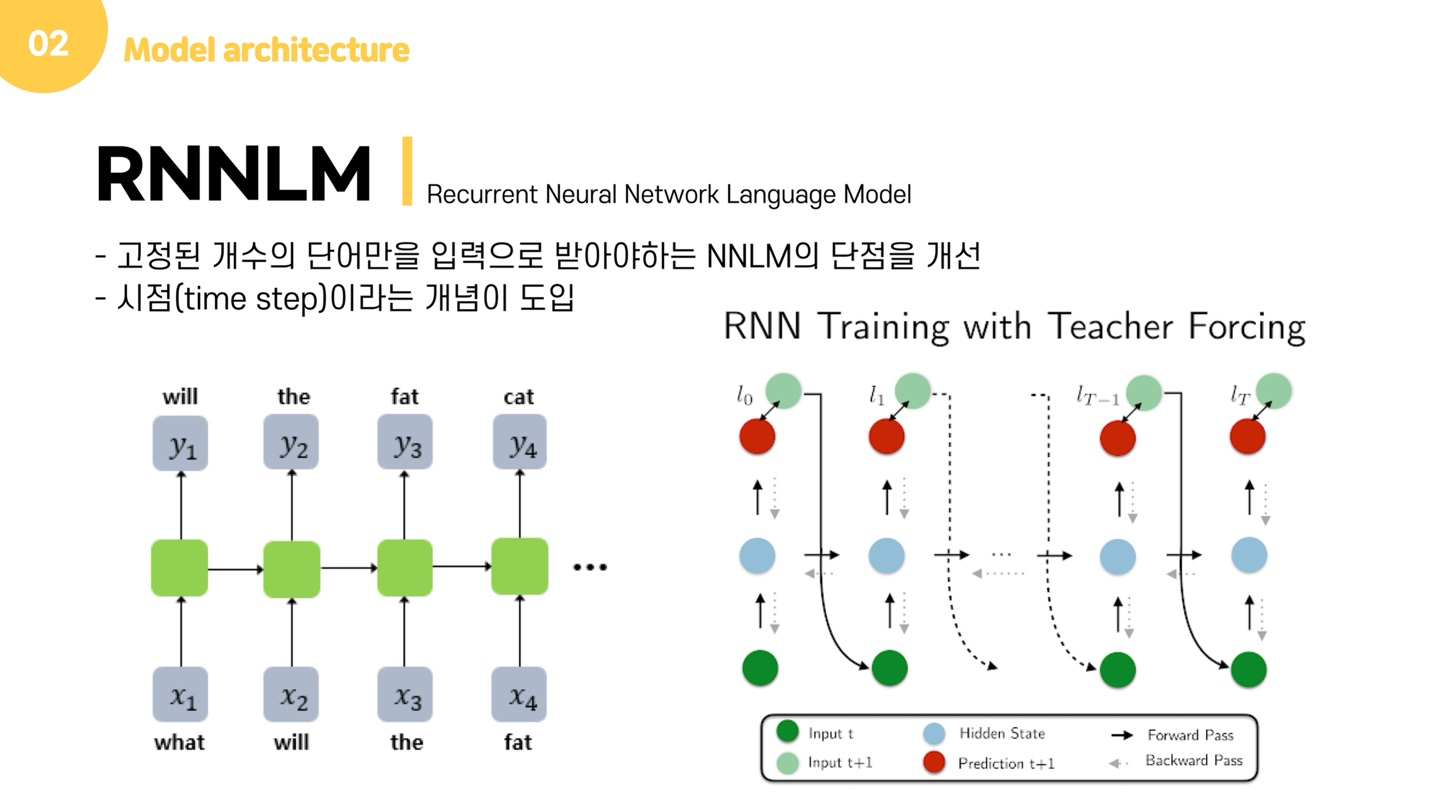
만약 what을 입력받았을 때 a라는 값을 예측했다고 합시다. 그러면 다음 입력층에는 a라는 단어가 들어갈까요? 아닙니다. teacher forcing이라는 RNN 훈련 기법을 사용하면 예측된 값과 상관없이 원래 정답인 값이 다음 입력층에 들어갑니다. 물론, 이전 시점의 출력을 다음 시점의 입력으로 사용하며 훈련시킬 수도 있지만, 한 번 잘못 예측하면 뒤까지 영향을 줄 수 있기 때문에 보다 효율적인 학습을 위해 teacher forcing을 사용한다고 합니다.

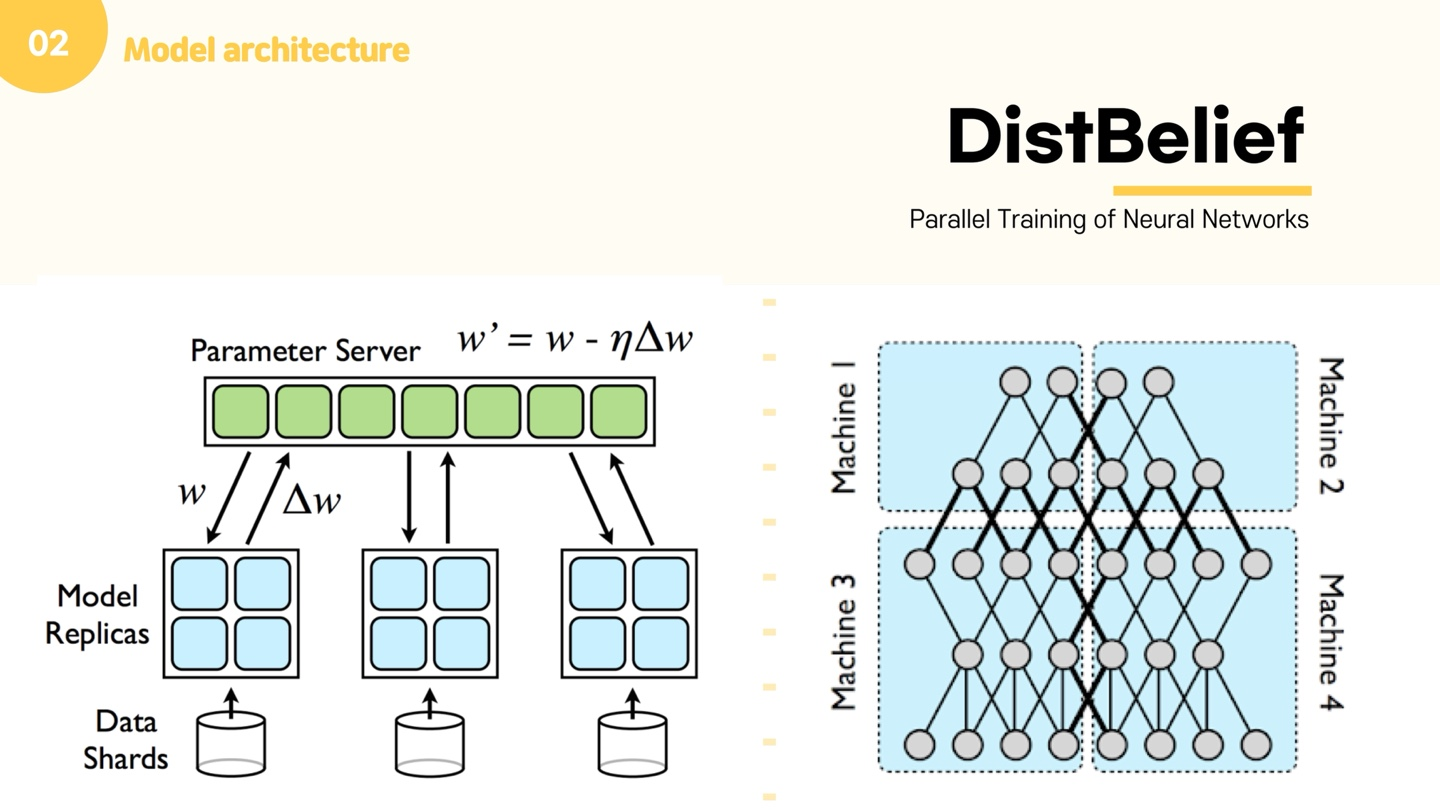
그럼 여기까지 NNLM과 RNNLM의 설명을 마치고, Distbelief에 대해 설명드리겠습니다. NNLM이 이제 큰 데이터를 계산하기 위해 도입된 방법인데, NNLM 모델 등의 딥러닝 모델이 발전하며, 계산량이 많아지고 메모리 요구량이 커져 한 대의 컴퓨터로는 모델이 돌아가지 않는 상황이 발생할 수 있습니다. 이때문에 다수의 컴퓨터가 이를 효율적으로 나누어 처리하기 위한 분산 처리 기술이 제안되었습니다. Distbelief는 구글의 1세대 분산 시스템으로, 수 십억 개의 파라미터를 가지는 대규모 딥 뉴럴 네트워크를 수천대의 컴퓨터에서 분산 트레이닝 할 목적으로 개발되었습니다. 5개의 계층으로 구성된 딥 뉴럴 네트워크를 4개의 모델로 분할하여 머신 1, 2, 3, 4에서 각기 실행합니다. 분할되지 않았다면 계산의 반복만으로 처리된 수 있지만, 뉴런 연결이 분할되었기에 뉴런은 그와 연결된 이전 뉴런으로부터 데이터와 가중치를 입력받아 계산한 결과를 연결된 다음 뉴런으로 전달해야 합니다. 그 때문에 굵은 검은색 선으로 머신 간 통신이 표시된 것을 확인할 수 있습니다. 왼쪽 그림을 설명해보면, 같은 모델이 쓰이기에 모델 레플리카를 만들고, 이를 공유되는 파라미터 서버를 통해 계속 파라미터가 업데이트 된다는 것을 의미합니다. Distbelief를 사용하면 100개 이상의 서로 다른 CPU에서 동시에 학습이 가능하다고 합니다.

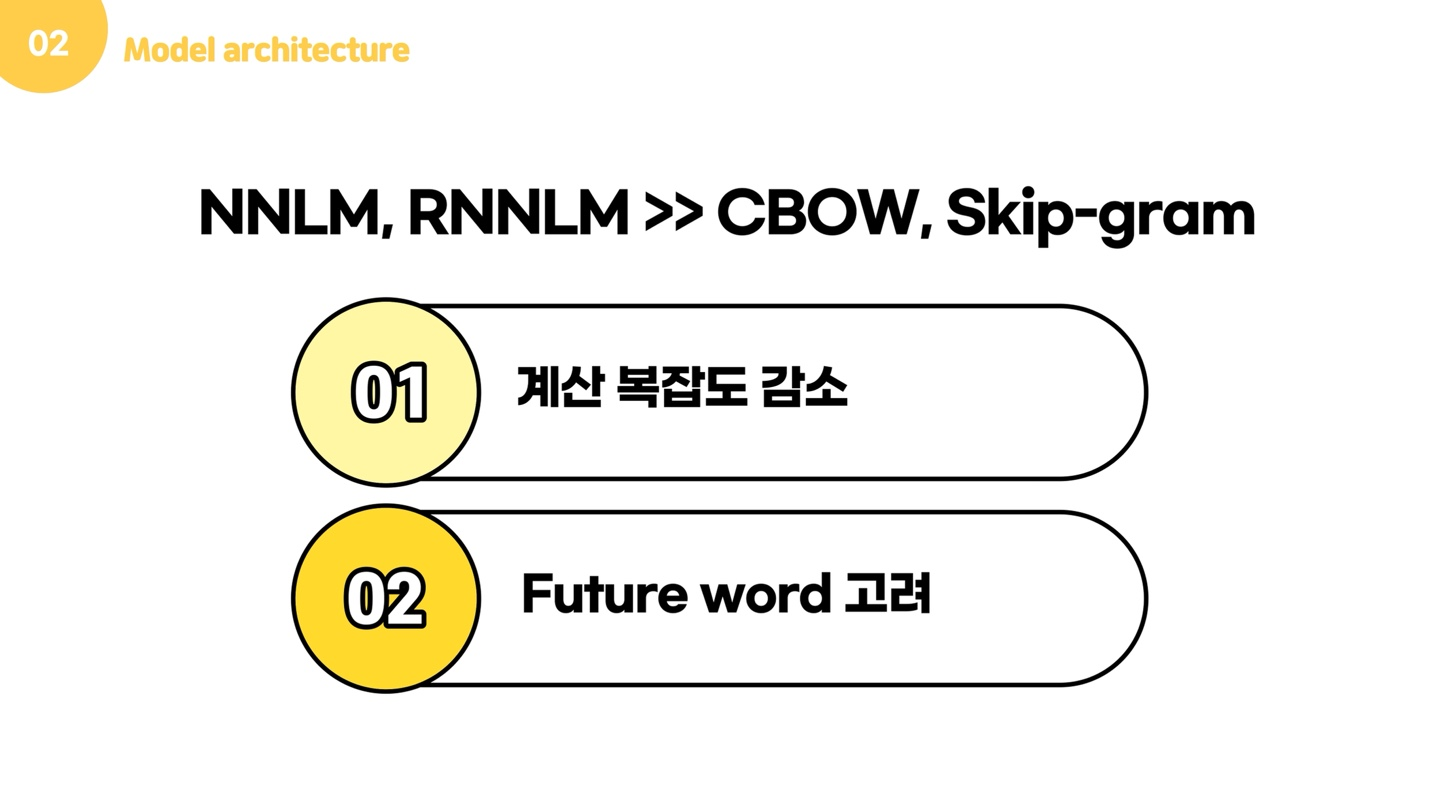
이제 본 논문에서 제안한 두가지 모델을 소개해드리고자 합니다. 본 논문은 계산 비용을 최소화하면서 distributed word vector를 학습할 수 있는 2가지 모델을 제안했는데요. 이 모델들이 가지는 이점은 크게 두가지입니다. 먼저 계산 복잡도에 대해 말씀드리면, 아까 살펴봤던 NNLM는 input, projection, hidden, output layer로 이루어져 있었고, 대부분의 비용이 non-linear hidden layer에서 발생했습니다. 본 논문에서는 이 문제를 해결하기 위해서 new log-linear model로 CBow와 skip-gram을 제안했는데요. Cbow와 skip gram은 비용이 많이 발생했던 non-linear hidden layer를 없애고, projection matrix 뿐만 아닌 layer까지 모든 단어들이 공유하게 한 모델입니다.
그리고 두번째 장점은 아까 두 모델은 history word, 즉 과거 단어들만 고려했지만, 이제는 future word도 고려가 가능하다는 점입니다.

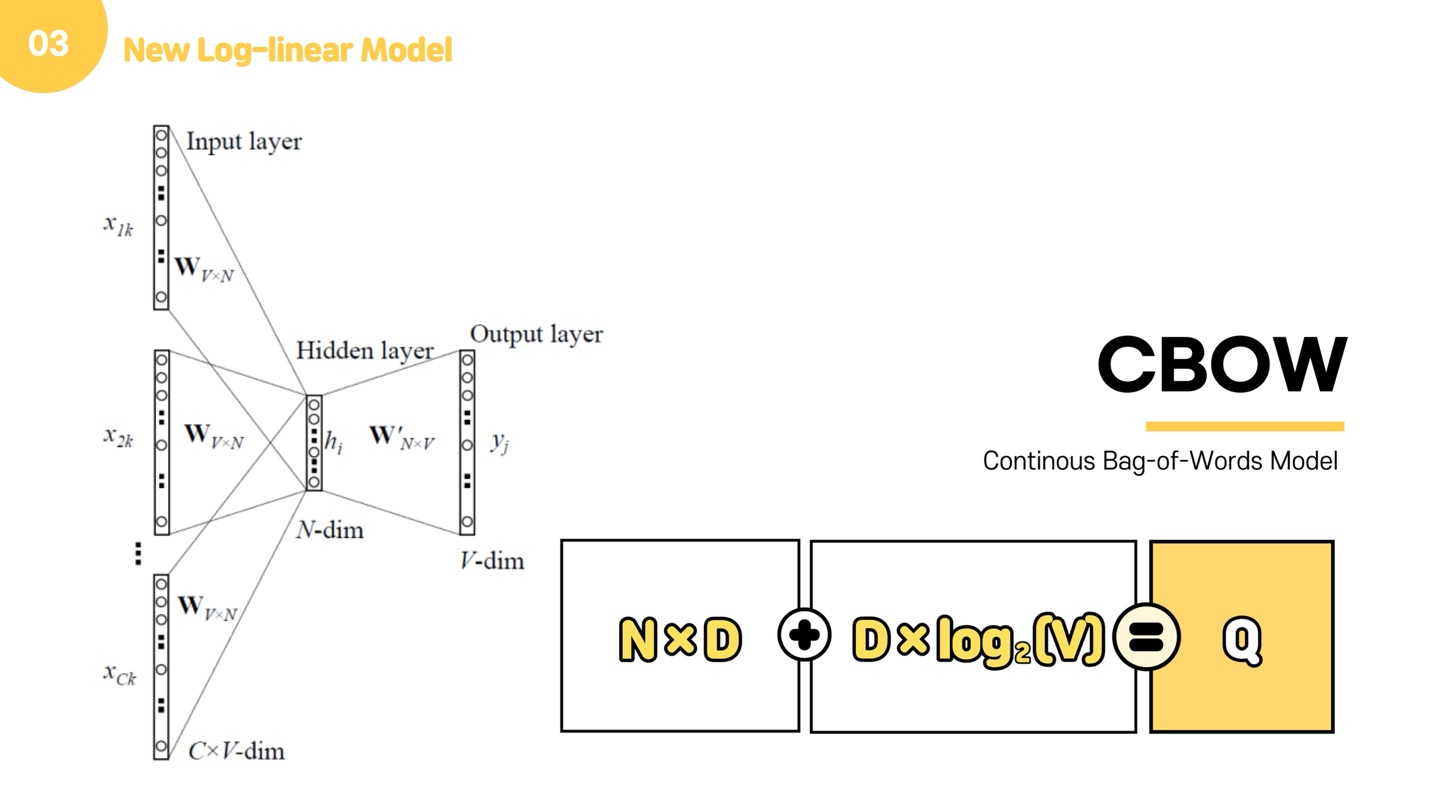
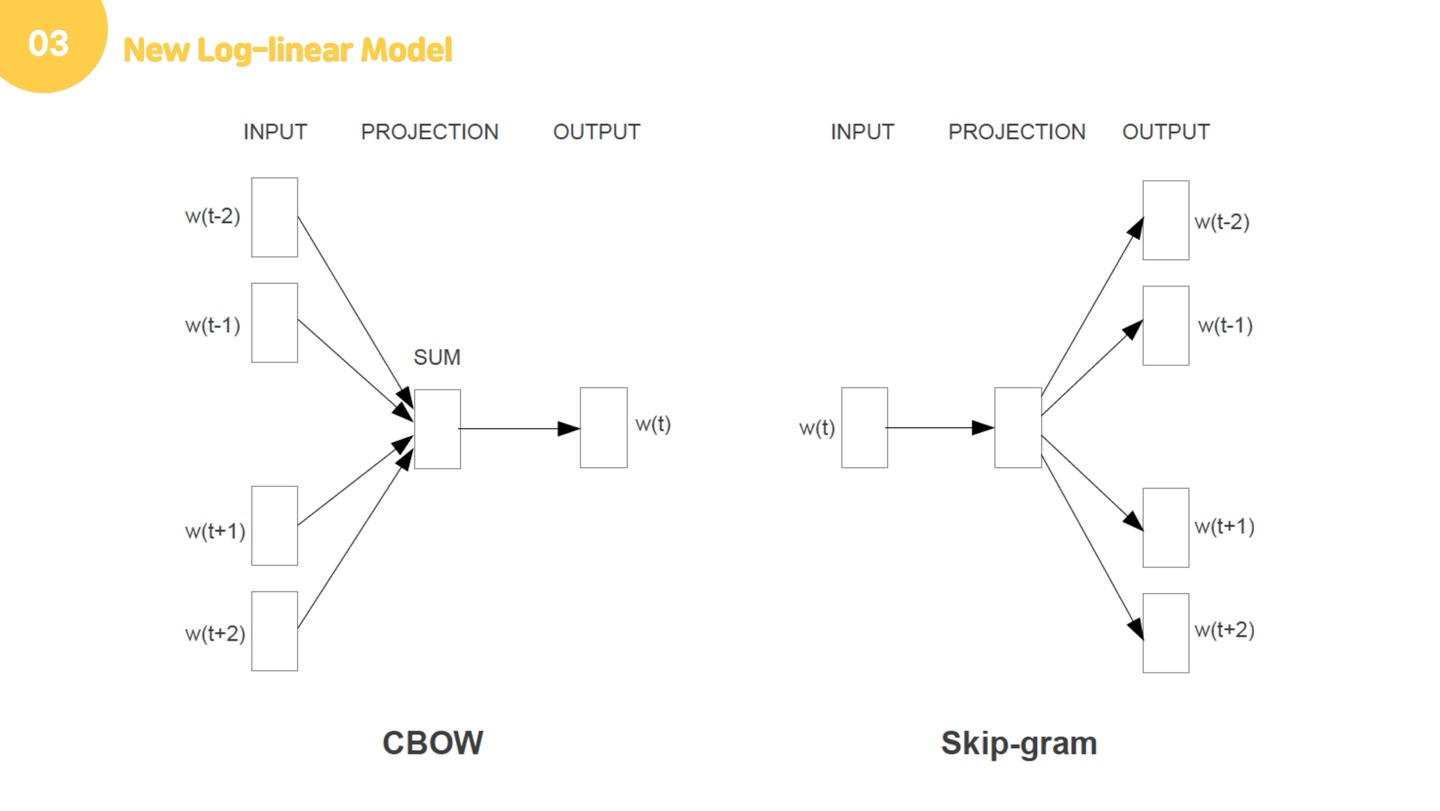
CBOW는 주변 문맥 단어(context word)로 타깃 단어(target word)를 맞추는 과정 학습하고, Skip-gram은 타깃 단어(target word)로 주변 문맥 단어(context word) 맞추는 과정 학습합니다. 이 두 모델은 아주 비슷한 구조를 가지고 있습니다. 먼저 Cbow먼저 설명하겠습니다.

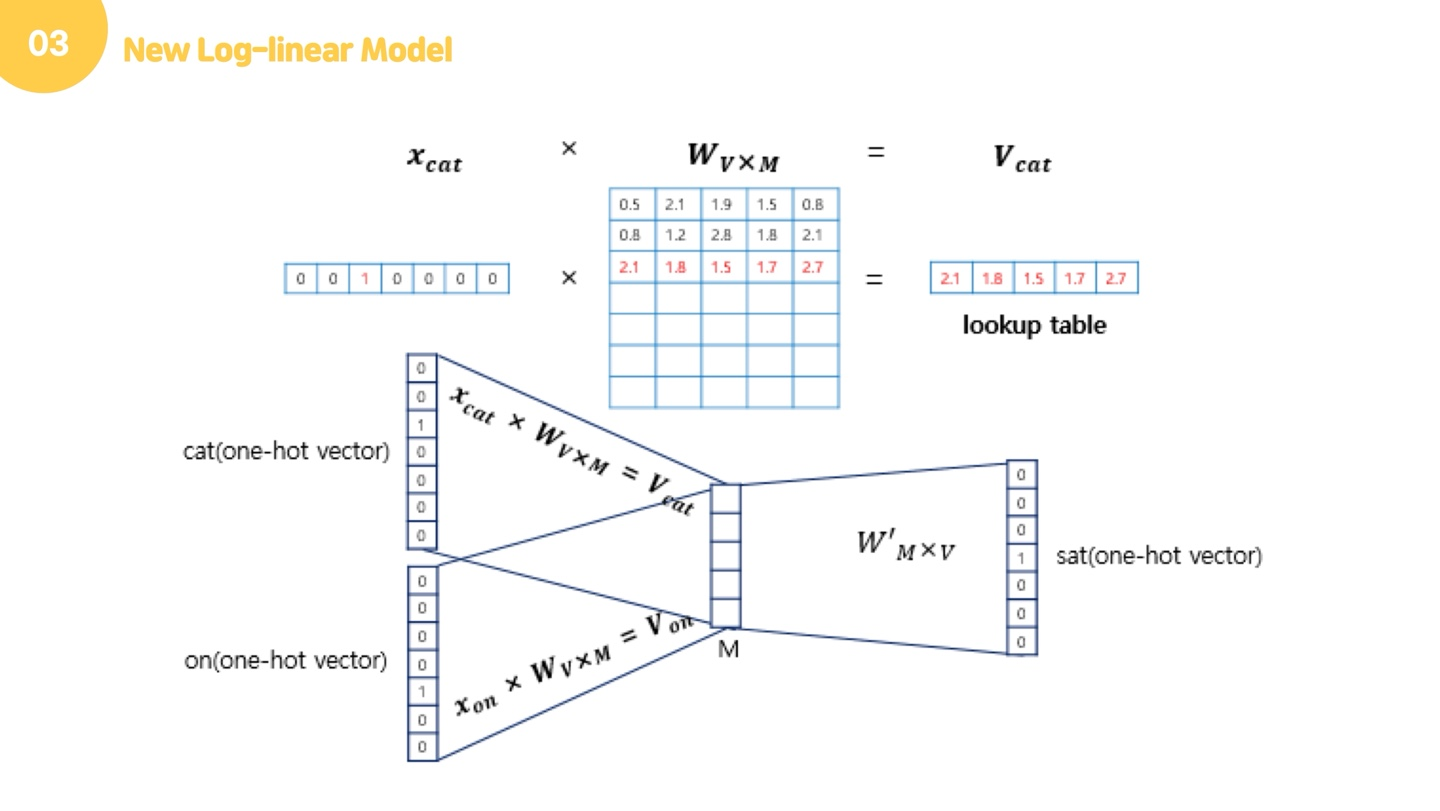
예를 들어 "The fat cat sat on the mat"라는 문장이 있다고 합시다. Cbow는 주변단어를 가지고 중심단어를 예측하는 모델입니다. 중심 단어를 예측하기 위해서 앞, 뒤로 몇 개의 단어를 볼지를 결정했다면 이 범위를 윈도우(window)라고 합니다. 예를 들어서 윈도우 크기가 2이고, 예측하고자 하는 중심 단어가 sat이라고 한다면 앞의 두 단어인 fat와 cat, 그리고 뒤의 두 단어인 on, the를 참고합니다. 윈도우 크기가 n이라고 한다면, 실제 중심 단어를 예측하기 위해 참고하려고 하는 주변 단어의 개수는 2n이 될 것입니다. 윈도우 크기를 정했다면, 윈도우를 계속 움직여서 주변 단어와 중심 단어 선택을 바꿔가며 학습을 위한 데이터 셋을 만들 수 있는데, 이 방법을 슬라이딩 윈도우(sliding window)라고 합니다. 그럼 예를 들어서 설명해드리겠습니다. 먼저 윈도우를 1로 정했다면, 주변단어인 cat과 on이 input layer에 원핫벡터로 들어갑니다. 이 때, 행렬 $W$ 의 크기는 단어의 개수 x 투사층의 크기입니다. 아까 NNLM에서 살펴봤던 것 처럼, 원핫벡터의 성질 때문에 이는 $W$ 행렬의 $i$ 번째 행을 그대로 참조해오는 것과 같습니다. 그래서 이 작업을 룩업 테이블이라고도 합니다.

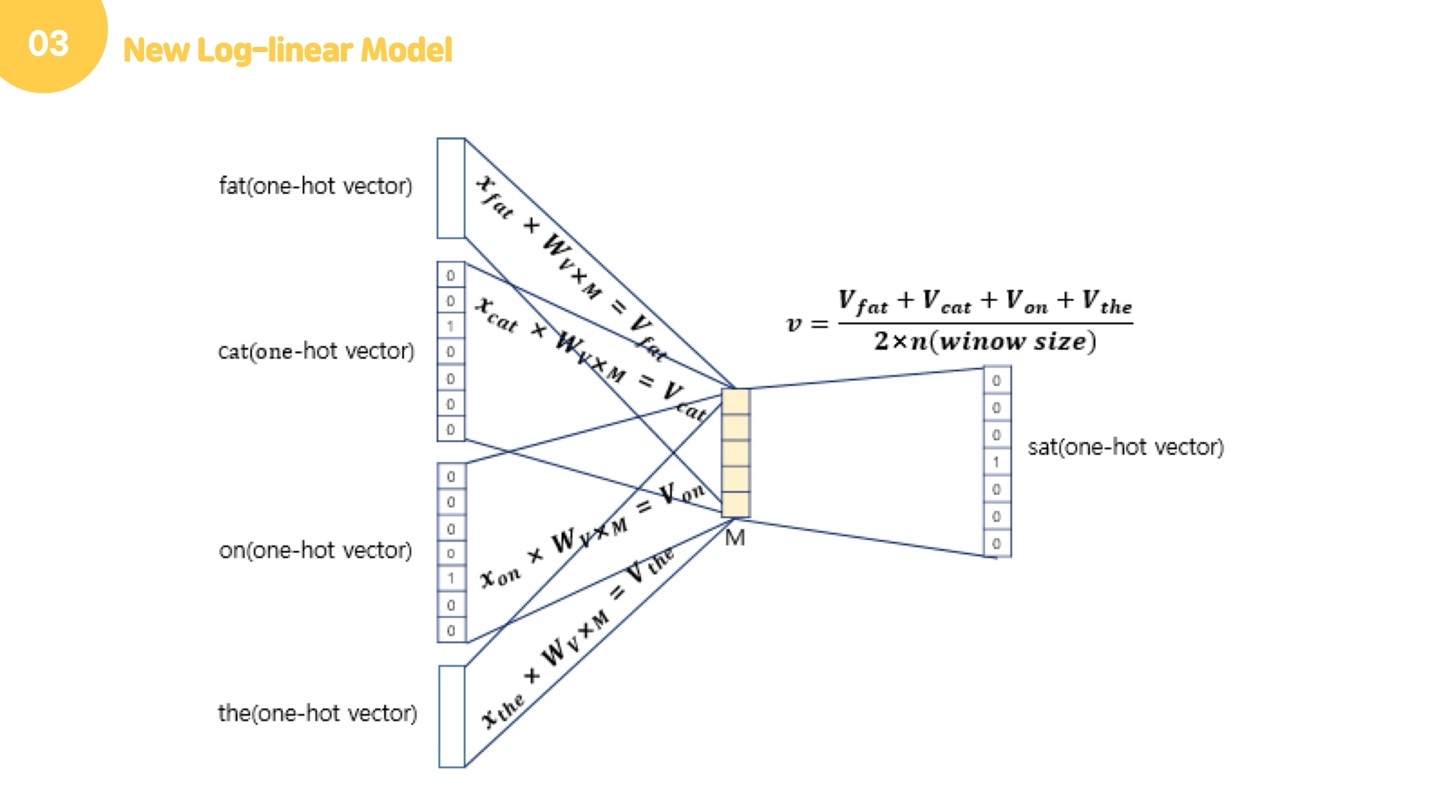
이렇게 각 주변 단어의 원-핫 벡터에 대해서 가중치 $W$ 가 곱해서 생겨진 결과 벡터들은 투사층에서 만나 이 벡터들의 평균인 벡터를 구하게 됩니다. 이제 우리가 구하고 싶은건 중심 단어 하나이기 때문에 2xwindow size로 벡터의 합을 나누어 평균을 구합니다.

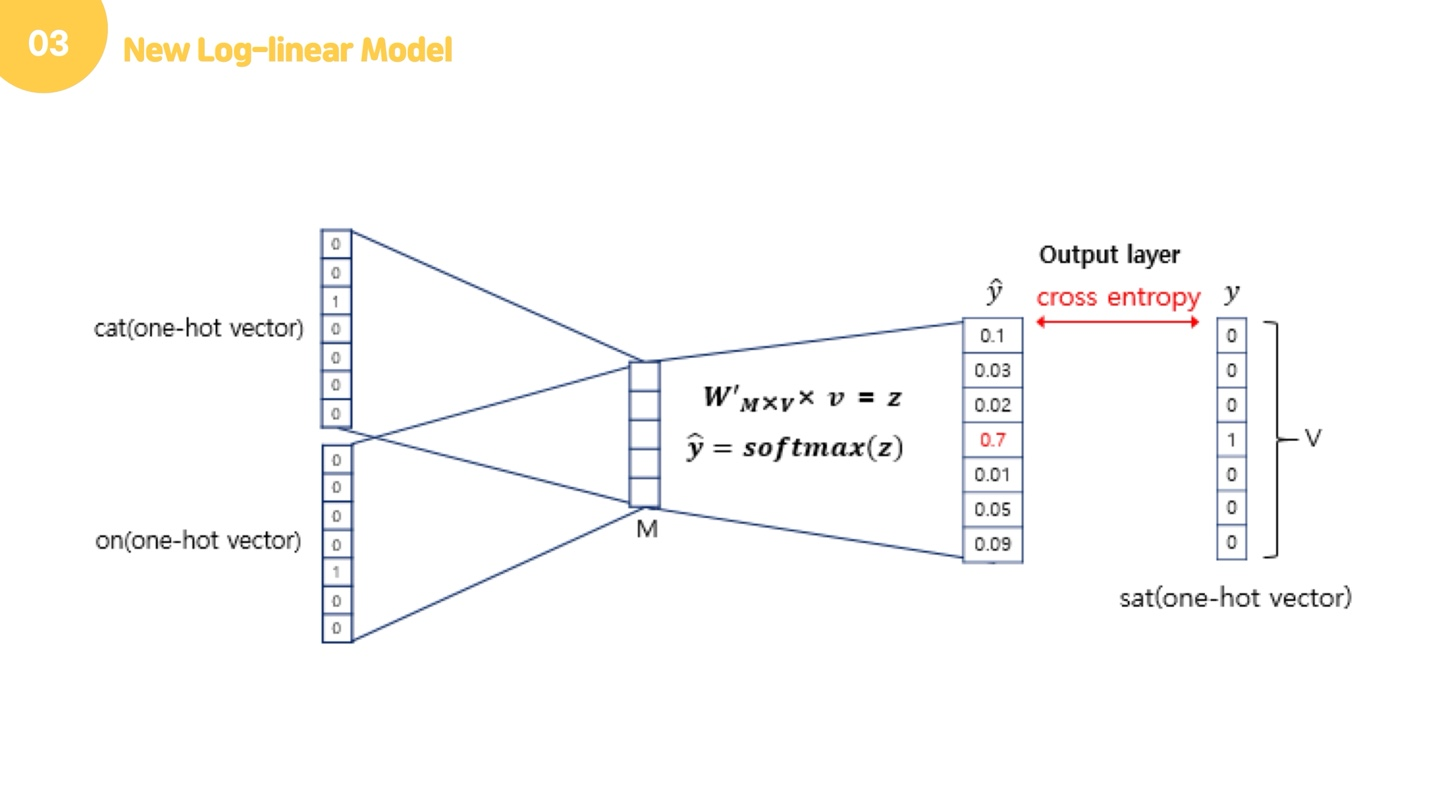
이렇게 구해진 평균 벡터에 softmax를 취해서 0,1의 실수로 바꿔줍니다. 이렇게 나온 벡터를 스코어 벡터라고 하고, 이 스코어 벡터는 중심단어의 원핫벡터의 값에 가까워져야 합니다. 이 오차를 줄이기 위해 loss function으로 cross entrophy 함수를 사용합니다.

근데 여기서 혹시, 제일 앞에서 one hot encoding이랑 분산 표현 설명드렸던거 기억나시나요? 사실 아까 nnlm할 때부터 계속 원핫벡터 이야기만 엄청 했는데 그럼 분산 표현을 왜 설명했는지 궁금하신 분이 있을 거에요.
사실, 여기서 가중치의 각 행이 곧 분산표현입니다. 그렇기 때문에 가중치를 잘 학습시키는게 굉장히 중요하고, 이 W벡터의 뉴런 수를 입력 층의 뉴런 수보다 적게하는게 굉장히 중요해요. 원핫인코딩보다 분산표현이 차원이 적어서 좋다했는데, W의 여기서의 M수를 V보다 크게 만들면 안되겠죠? 이 가중치 값의 학습을 통해 우리는 단어의 정보를 간결하게 담을 수 있게 됩니다.

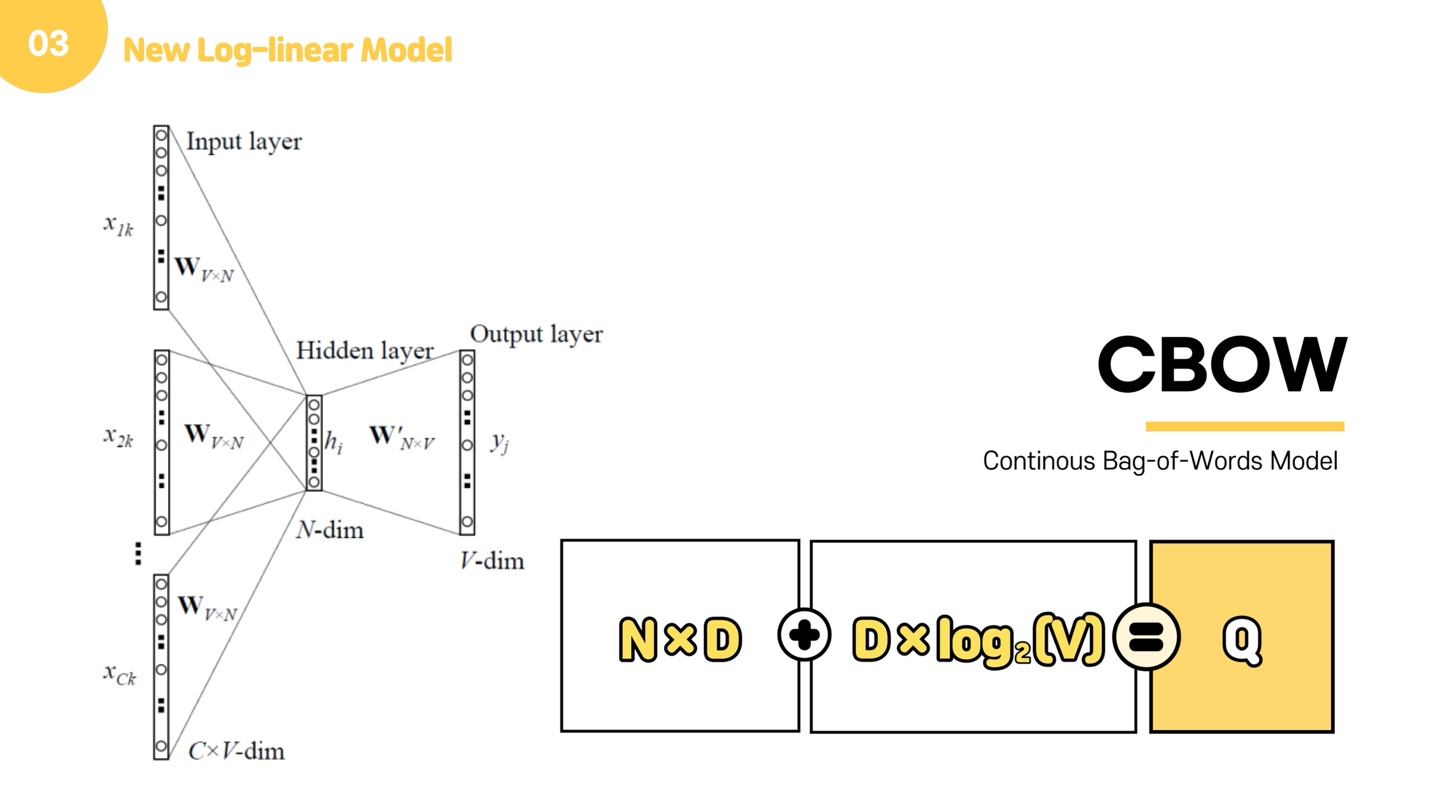
이제 skip gram을 설명드리겠습니다. skip-gram은 중심단어를 넣어서 주변단어를 예측한다는 점만이 다른데요. 아까랑 다 같은 구조지만, 다른 것은 중심 단어 하나만 들어가기 때문에 평균을 구하는 과정이 없다는 것입니다. 평균을 구하는 과정 없이 주변 단어에 대해 모델을 돌려주면 되고, 안의 로직은 cbow와 동일합니다.

그럼 앞서 소개드렸던 모델들의 계산 복잡도를 정리해드리겠습니다. 계산 복잡도를 구해보면 NNLM은 250만으로 굉장히 높은데에 비해서, CBow와 Skip-gram은 낮은 걸 볼 수 있습니다. 아까 NNLM과 RNNLM이 non-linear hidden layer에서 계산 비용이 많이 발생했다고 했는데요, 보면 nxmxh, hxh가 hidden layer로 넘어갈 때 발생하는 계산 비용입니다. CBow와 Skip-gram은 hidden layer로 넘어가는 과정이 없어지면서 계산 비용이 확 줄어든 것을 확인할 수 있고, 본 논문에서 말하고자 한 효율적인 학습이 이뤄지는 것을 볼 수 있습니다.

그럼 이제 결과를 소개해드리겠습니다. 모델 간 비교를 위해 analogy reasoning task를 이용합니다. Analogy Reasoning Task는 어떤 단어의 Pair, 예를 들어 (Athens, Greece) 라는 Pair가 주어졌을 때, 다른 단어 Oslo를 주면 이 관계에 상응하는 다른 단어를 제시하는 방식의 시험입니다. 이 관계에는 semantic, 즉 문맥적인 관계 5가지와 문법적인 관계 9가지로 이루어져 있습니다. 벡터를 잘 학습했다면 vector(Greece) – vector(Athens) + vector(Oslo)를 한 후 이 벡터에 가장 가까운 벡터를 찾으면 노르웨이가 나올 것입니다.

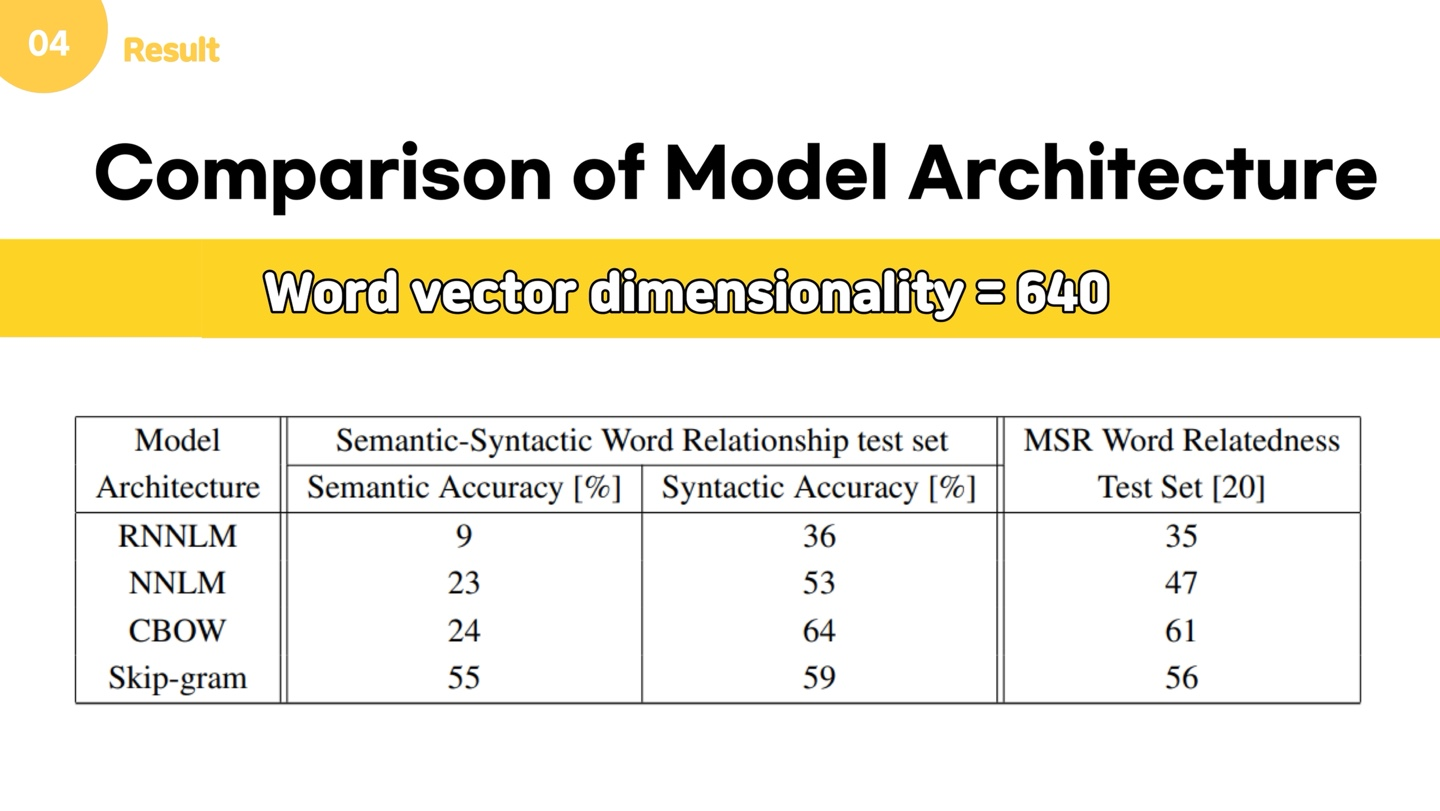
위는 단어 벡터 길이를 640으로 하고 다양한 모델을 이용하여 학습시켰을 때의 결과입니다. 보다시피 RNNLM과 NNLM에 비해 CBow와 Skip-gram이 Semantic, Syntactic 문제에 대해 훨씬 더 좋은 결과를 내는 것을 알 수 있습니다. 또한 CBow와 Skip-gram을 비교해보았을 때, Skip-gram이 Syntactic 문제의 정확도는 조금 떨어지기는 하지만 두 문제 모두에서 전반적으로 높은 정확도를 보였습니다.

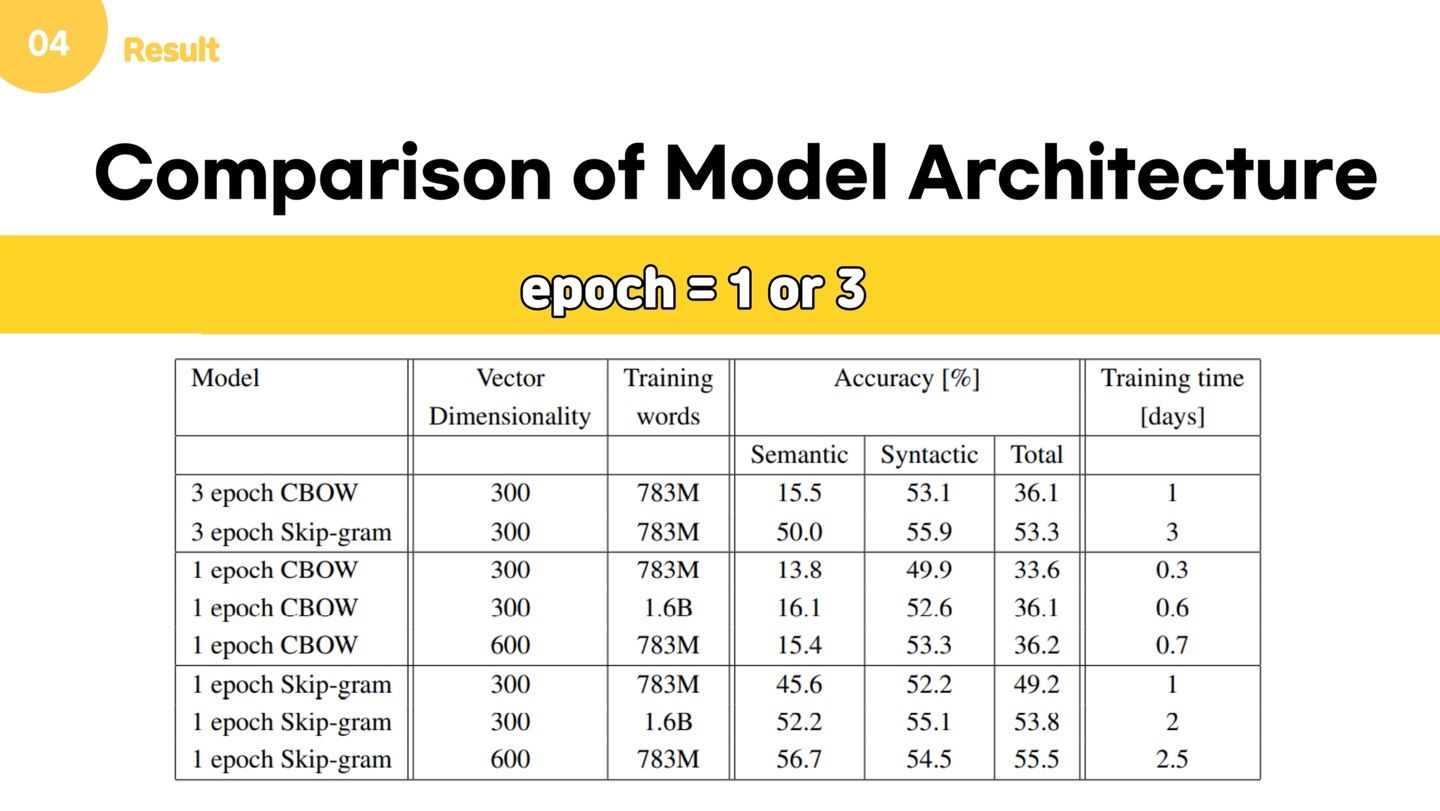
또한, 상대적으로 적은 데이터를 여러번의 epoch 를 통해 학습하는 것보다, 많은 데이터를 이용해 1번의 epoch만 학습하는 것이 더 좋은 성능을 제공한다는 것을 알 수 있었습니다.