[백준] 14719번: 빗물

조소복·2022년 11월 30일

Java 골드V 백준 자바

문제

2차원 세계에 블록이 쌓여있다. 비가 오면 블록 사이에 빗물이 고인다.

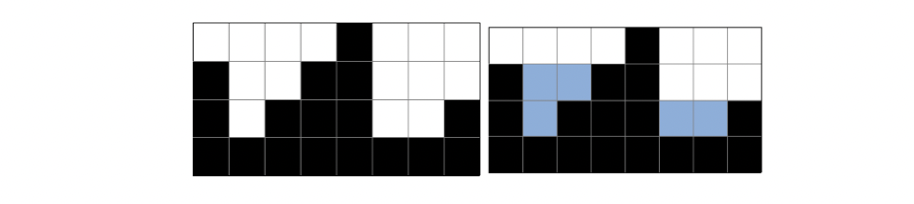
비는 충분히 많이 온다. 고이는 빗물의 총량은 얼마일까?

입력

첫 번째 줄에는 2차원 세계의 세로 길이 H과 2차원 세계의 가로 길이 W가 주어진다. (1 ≤ H, W ≤ 500)

두 번째 줄에는 블록이 쌓인 높이를 의미하는 0이상 H이하의 정수가 2차원 세계의 맨 왼쪽 위치부터 차례대로 W개 주어진다.

따라서 블록 내부의 빈 공간이 생길 수 없다. 또 2차원 세계의 바닥은 항상 막혀있다고 가정하여도 좋다.

출력

2차원 세계에서는 한 칸의 용량은 1이다. 고이는 빗물의 총량을 출력하여라.

빗물이 전혀 고이지 않을 경우 0을 출력하여라.

예제 입력 1

4 4
3 0 1 4

예제 출력 1

예제 입력 2

4 8
3 1 2 3 4 1 1 2

예제 출력 2

예제 입력 3

3 5
0 0 0 2 0

예제 출력 3

힌트

힌트 1:

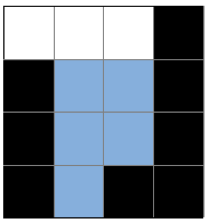
힌트 2:

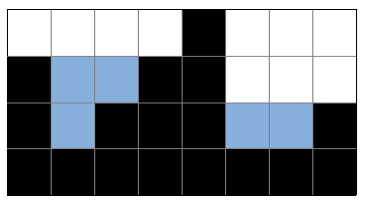
힌트 3:

문제 풀이

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class BJ14719 {
    public static void main(String[] args) throws IOException {
        BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st=new StringTokenizer(br.readLine());

        int H=Integer.parseInt(st.nextToken());
        int W=Integer.parseInt(st.nextToken());

        int[] height=new int[W];
        int answer=0;
        int max=-1;
        int max_idx=0;

        st=new StringTokenizer(br.readLine());
        for(int i=0;i<W;i++){
            height[i]=Integer.parseInt(st.nextToken());
            if(max<height[i]){
                max=height[i];
                max_idx=i;
            }
        }

        int start=0;
        for(int i=0;i<max_idx;i++){
            if(height[i]>=height[start]){
                start=i;
            }
            else{
                answer+=height[start]-height[i];
            }
        }
        start=W-1;
        for(int i=W-1;i>max_idx;i--){
            if(height[i]>=height[start]){
                start=i;
            }
            else{
                answer+=height[start]-height[i];
            }
        }

        System.out.println(answer);
    }
}

각 높이가 평평해지도록 빗물로 빈 공간을 채우는 문제이다. 즉, 현재 위치보다 높은 벽을 만나게 되면 기준이 된 높이까지 모두 빗물을 채워주는 것이다.

처음 시작하는 기준이 되는 벽의 위치를 저장한다.
기준벽의 높이보다 높거나 같은 높이의 벽을 만나면 기준벽의 위치를 해당 벽의 위치로 변경한다.
기준벽의 높이보다 낮다면 기준벽의 높이 - 현재 벽의 높이 값만큼 빗물을 채워준다.

하지만 이때, 가장 높은 벽을 만나고 해당 위치를 기준으로 잡으면 가장 높은 벽의 다음은 빗물을 채울 수 없기 때문에

가장 높은 벽을 기준으로 왼쪽, 오른쪽을 나누어 계산한다.

가장 높은 벽과 기준 세우기

int[] height=new int[W];
int max=-1;
int max_idx=0;

st=new StringTokenizer(br.readLine());
for(int i=0;i<W;i++){
    height[i]=Integer.parseInt(st.nextToken());
    if(max<height[i]){
        max=height[i];
        max_idx=i;
    }
}

max보다 높은 벽을 만나면 해당 벽의 위치와 높이로 갱신해준다.

왼쪽

int start=0;
for(int i=0;i<max_idx;i++){
    if(height[i]>=height[start]){
        start=i;
    }
    else{
        answer+=height[start]-height[i];
    }
}

기준벽을 우선 인덱스 0 위치의 벽으로 잡아준다.

그런 다음 반복문을 가장 높은 벽의 위치만큼 돌리고

기준벽의 높이보다 i 인덱스의 벽의 높이가 높거나 같다면 start 값을 i로 갱신해준다.

즉, 기준벽을 바꿔주는 작업을 한다.

반대로 기준벽보다 낮은 높이를 만나게 되면 기준벽의 높이 - i번째 위치의 벽의 높이 만큼 빗물을 채워준다.

즉, answer 값을 더해준다.

오른쪽

start=W-1;
for(int i=W-1;i>max_idx;i--){
    if(height[i]>=height[start]){
        start=i;
    }
    else{
        answer+=height[start]-height[i];
    }
}