Deep Resiaual Learning for Image Recognition
Abstract
딥러닝 모델은 layer가 깊어질수록 학습시키기 어렵다.
배경
네트워크를 깊이 쌓을수록 성능이 증가하네!!!
Imagenet 우승 모델을 보면 convolutional neural network를 깊게 쌓으면서 이미지 분류의 성능이 많이 증가한 것을 알 수 있다. 네트워크를 깊이 쌓으면 low/mid/high-level 의 feature 즉, 풍부한/다양한 feature map을 얻을 수 있기 때문이다. 네트워크의 깊이(depth)가 모델 성능에 큰 영향을 미치는 것 또한 알 수 있다.
네트워크를 정도껏 깊이 쌓아야 성능이 증가하는군.....
"Is learning better networks as easy as stacking more layers?" "layer를 깊이 쌓기만 하면 네트워크의 성능이 좋아지는가?" 궁금증이 생긴다.
위의 질문에 "그렇다"라고 답하기 어려운 여러가지 이유가 있다.
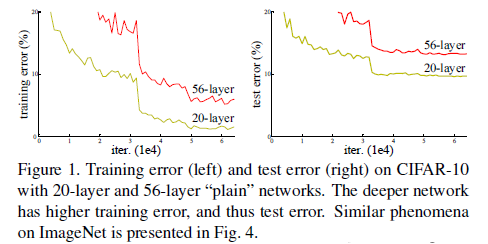
1) Vanishing/exploding gradients -> 네트워크를 초기화할 때 정규화함으로써 해결 (normalized initialization & intermediate normalization layers)
Vanishing gradients : sigmoid 활성화 함수를 사용하면 layer가 깊어질수록 역전파시 기울기가 0에 가까워져 학습이 잘 되지않는 문제
2) 깊은 네트워크가 수렴할 때 degradation problem : layer가 일정수준 이상 깊어지면 성능이 감소할 수 있음(training error가 증가함)
또한 네트워크가 깊어지면 학습해야할 parameter의 수도 급증한다!
핵심 아이디어 : Residual Learning
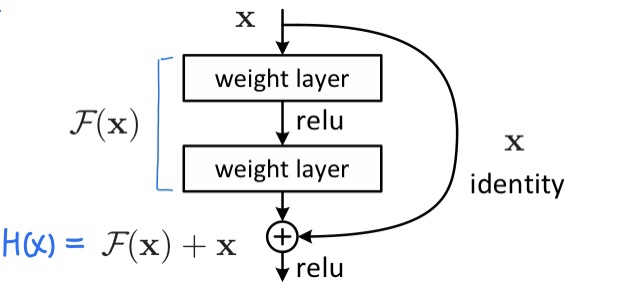
논문의 저자들은 단순히 여러개의 convolution layer를 이어붙이는 것은 한계라고 생각해 Residual Block을 제안했다.
위의 그림에서 x는 입력값, F(x)는 입력에서 변화한 부분을 의미하며, 우리가 학습하고 싶은 것은 H(x)이다.
H(x)를 학습하는 것 보다 입력값에서 얼마나 변화했는지를 의미하는 F(x)를 학습하는게 더 쉽다.
H(x) = F(x) + x -> F(x) = H(x) - x
따라서 H(x) 대신 F(x)를 학습하도록 한다.
가정 : 1) direct mapping 보다 residual mapping이 쉬울 것이다. 2) 대부분의 layer가 잘 동작하려면 layer의 출력이 identity에 가까워져야 한다.
이 때 identity mapping이 최적해라면 F(x) = H(x) - x = 0 이므로 H(x) = x 이다.
H(x)를 x로 매핑시키는 것이 학습의 목표이다.
장점
- 기존의
H(x)를 특정 값으로 근사시키는 학습 방법은 특정 값을 모르기 때문에 어려움이 있지만,F(x)는H(x) = x라는 목표가 있기 때문에 학습이 수월해진다. - 단순히 shortcut 구조만 기존 네트워크에 추가하면 되기 때문에 구조가 복잡하지 않고, 학습 파라미터도 증가하지 않는다.
- 깊은 신경망을 구성해도 vanishing gradients 문제가 발생하지 않는다.
Network Architecture
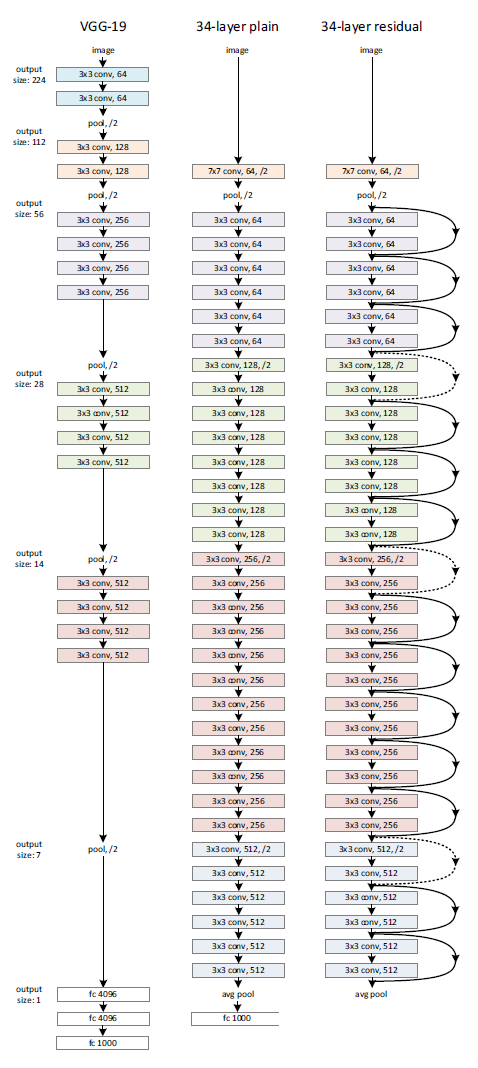
왼쪽 : VGG-19 모델
중앙 : residual이 없는 34 layer 모델 (동일한 layer의 residual network와 비교하기 위해서)
오른쪽 : residual이 있는 34 layer 모델, convolution filter를 2개씩 묶어서 residual function 형태로 학습을 진행함.
VGG에서 제안된 내용을 기반으로 네트워크를 구성했다.
1) 3*3 크기의 작은 필터를 사용함
-> 출력 shape을 맞추기 위해 모든 레이어에서 동일한 개수의 필터를 사용함
-> 피쳐맵 사이즈가 절반으로 줄어들면 다음 레이어에서 필터의 개수를 2배로 만들어줌 -> 레이어마다 time complexity를 보존함
2) 별도의 pooling layer는 사용하지 않고 convolution layer에서 stride=2로 설정함
오른쪽 그림에서 점선은 입출력의 크기가 맞지 않아 크기를 맞추는 technique을 사용한 경우이다.
-> 입출력 dimension이 같은 경우 : identity mapping
-> 입출력 dimension이 같은 경우 : 1) 패딩을 추가해 identity mapping 2) projection shortcut 사용
Implementation
ImageNet 데이터를 224*224 크기로 랜덤 크롭
Batch Normalization(BN) : 매 convolution layer마다 적용함
Learning Rate Decay : 0.1로 초기화 후 에러율이 감소하지 않으면 1/10로 감소
Iteration : 60x10^4번
Weight Decay, Momentum : 0.0001, 0.9
Dropout : 사용 X
Experiments
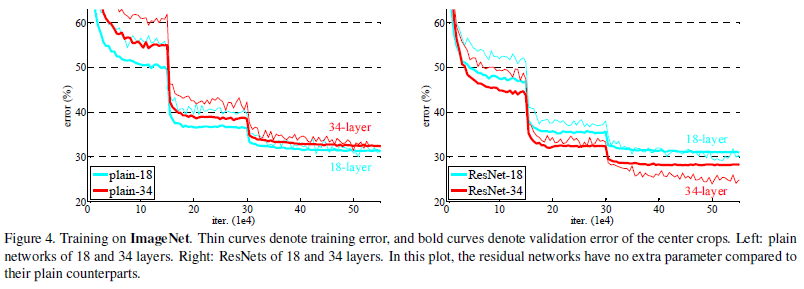
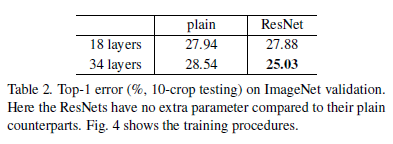
Plain Network에 비해 Residual Network는 레이어 수가 증가해도 성능이 증가하는 것을 확인할 수 있다. 수렴 속도 또한 빠른 것을 확인할 수 있는데, 빠른 수렴 속도는 최적화를 쉽게 만들어준다.
논문의 저자들은 layer가 깊어질수록 성능을 저하시키는 원인이 vanishing gradients가 아닐 것이라고 말했다. 또한 forward, backward 학습 모두에서 signal이 감소하지 않음을 확인했다.
그들은 exponentially low convergence rate, 수렴율이 기하급수적으로 낮아지는 문제 때문이라고 설명했다. 최적화 기법에서 나오는 개념으로 수렴 난이도를 의미하는 척도로 수렴을 위해 필요한 에폭 등을 의미한다.
참고자료 :
딥러닝 홀로서기 ResNet
나동빈 꼼꼼한 딥러닝 논문 리뷰
