벡터 공간의 기저와 차원, 정규 직교 기저, 그람-슈미트 정규직교화

벡터 공간의 기저(basis)와 차원(dimension)

벡터 공간 S에 있는 벡터의 집합 $\{x_1,x_2,\dots,x_n\}$에 대하여 다음을 만족하면 $\{x_1,x_2,\dots,x_n\}$은 S의 기저(basis)이다.
1. $\{x_1,x_2,\dots,x_n\}$ spans the vector space S.
2. $\{x_1,x_2,\dots,x_n\}$ is linearly independent.

• 즉, S에 속하는 모든 벡터는 $\{x_1,x_2,\dots,x_n\}$의 선형 결합으로 표현되며, $\{x_1,x_2,\dots,x_n\}$ 중 어느 벡터도 다른 벡터의 선형 결합으로 표현되지 않으면, S의 기저라고 할 수 있다.
• 이 기저에 속하는 벡터들의 갯수를 차원(dimension)이라고 한다.
  $dim(S) = n$
• 벡터 공간의 기저는 unique하지 않지만, 모든 기저는 벡터들의 갯수 즉, 차원은 동일하다.

Theorem

1. 벡터 공간 S의 기저에 포함된 벡터의 수는 일정하다.
2. 벡터 공간 S의 차원이 m이고 벡터 집합 $B=\{x_1,x_2,\dots,x_m\}$ ($B \subset S$) 가 독립이면, B는 S의 기저이다.
3. 벡터 집합 $B=\{x_1,x_2,\dots,x_m\}$가 벡터공간 S의 생성 집합이고 S의 차원이 m이면, B는 선형 독립이고 S의 기저이다.

• 생성 집합: 벡터 공간 S에 포함되는 m개의 벡터로 이루어진 집합 $\{x_1,x_2,\dots,x_m\}$에 대하여 S에 포함되는 모든 벡터가 $\{x_1,x_2,\dots,x_m\}$의 선형 결합으로 표현될 때, 이 집합을 S의 생성 집합(spanning set)이라고 한다.

4. 벡터들의 집합 $B=\{x_1,x_2,\dots,x_m\}$가 벡터 공간 S의 기저이면, S에 속하는 모든 벡터 s에 대하여 $s=\alpha_1 x_1 + \cdots + \alpha_m x_m$을 만족하는 벡터 $\alpha=(\alpha_1, \dots,\alpha_m)$가 존재한다.

기저(basis)와 좌표(coordinates)

$\{x_1,x_2,\dots,x_m\}$이 벡터 공간 S의 기저라면, S에 속하는 임의의 벡터 x는 다음과 같이 고유한 표현을 가진다.

여기서 $\alpha_1, \alpha_2, \dots , \alpha_n$는 스칼라 계수이며, 이를 $\{x_1,x_2,\dots,x_m\}$라는 기저에 대한 x의 좌표(coordinates)라고 부른다.

• 예시) 2차원 벡터 공간 $\mathbb{R^2}$에서 기저 $\{(1,0), (0,1)\}$가 주어진 경우, 벡터 $(3,4)$는 다음과 같이 유일하게 표현된다.
  $(3,4) = 3 \cdot (1,0) + 4\cdot (0,1)$
  여기서 3과 4가 바로 $(1,0), (0,1)$에 대한 $(3,4)$의 좌표이다.

정규 직교 기저, orthonormal basis

• Definition 1.
  두 벡터 $x$, $y$에 대하여 다음 두 조건을 만족한다면, 이 두 벡터는 정규 직교 벡터(orthonormal vector, orthogonal+normal)라고 한다.

  $\|x\|=\|y\|=1$
  $x^{\prime}y=\space <x,y> \space=0$

• Definition 2.
  벡터 공간 S의 기저 B를 이루는 벡터들이 다음의 조건을 만족할 때, B를 정규 직교 기저(orthonormal basis)라고 한다.

다르게 표현하면 아래와 같다.

• 벡터 공간 S의 기저 B를 이루는 벡터 $x_1, \dots, x_n$가 아래의 조건을 만족한다면, 정규 직교 기저이다.
  $<x_i, x_j> = \begin{cases} 0 & \mathrm{if} \space i \neq j \\ 1 & \mathrm{if}\space i = j\end{cases}$

Theorem

$\{x_1, \dots, x_n\}$를 벡터 공간 S의 정규 직교 기저라고 할 때, 모든 $x \in S$에 대하여 아래가 성립한다.

---

그람-슈미트 정규직교화 (Gram-Schmidt orthonormalization)

일반적인 기저로부터 정규 직교 기저를 만드는 방법이다.

• $\{x_1, \dots, x_n\}$를 벡터 공간 S의 기저라고 한다면, S의 직교 기저(orthogonal basis) $y_1, y_2, \dots y_n$는 다음과 같이 구할 수 있다.
  $y_1 =x_1$
  $y_2=x_2-\frac{<x_2,y_1>}{<y_1,y_1>}y_1$ : $x_2$를 $y_1$에 정사영한 벡터
  $\vdots$
  $y_n=x_n-\frac{<x_2,y_1>}{<y_1,y_1>}y_1-\cdots-\frac{<x_n,y_{n-1}>}{<y_{n-1},y_{n-1}>}y_{n-1}$
  
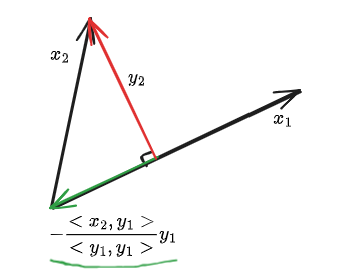
• 이 $y_i$으로 아래의 정규화 식을 이용하여 정규 직교 기저 $\{z_1, \dots,z_n \}$를 구할 수 있다.
  $z_i=\frac{1}{\|y_i\|}y_i$