1. 열공간(column space)과 행공간(row space)

• $m\times n$ 행렬 $A$
  
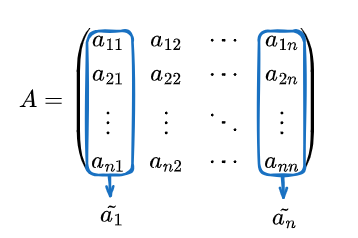
• n개의 열벡터에 의해 생성되는 $\mathbb{R}^m$의 부분 공간을 A의 열공간(column space)이라고 한다.
• m개의 행벡터에 의해 생성되는 $\mathbb{R}^n$의 부분 공간을 A의 행공간(row space)이라고 한다.

ex)

column space와 row space는 아래와 같다.

2. 행렬의 계수, rank

$rank(A) = r(A) =$ 행공간의 차원 $=$ 열공간의 차원

• 즉, 행 벡터들(또는 열 벡터들) 중에서 선형 독립(linearly independent)하는 벡터들의 갯수를 행렬의 계수(rank)라고 한다.
• 행렬 $A$가 $n\times n$ 정사각행렬이고 $dim(A)=n$ 일 때,
  $A$를 정칙행렬(regular matrix), 완전 계수 행렬(full rank matrix), 또는 비특이행렬, 가역행렬(nonsingular matrix)이라고 한다.

nonsingular, singular, inverse

• nonsingular matrix (가역행렬, 비특이행렬): 역행렬이 존재하는 행렬
  A nonsingular matrix $A$ has a unique inverse, denoted by $A^{-1}$, with the property that
  $AA^{-1}=A^{-1}A=I$
• singular matrix (특이행렬): 역행렬을 갖지 않는 행렬
  If $A$ is square and less than full rank, then it does not have an inverse and is said to be singular.

Theorem

$A$ : $m\times n$ 행렬
① $rank(A) = rank(A^{\prime})$
② $rank(A) \le min(m,n)$
③ $rank(AB) \le min(rank(A), rank(B)) \quad$ for any $n \times p$ matrix $B$

• 

④ $rank(AB) = rank(A) \quad$ for any $n\times n$ nonsingular matrix $B$

• 

⑤ If $A$ is an $m\times m$ matrix, then $|A| = 0 \Leftrightarrow rank(A) < m$

• $A$의 행렬식이 0이 아니라면, $rank(A)=m$

⑥ $rank(AA^{\prime})=rank(A^{\prime}A)=rank(A)$
⑦ If $A$ is idempotent ($A^2=A$), then $rank(A)=trace(A)$

• 행렬 $A$가 멱등행렬이라면, $A$의 계수는 $A$의 대각합과 같다.