Linear models in statistics

앨빈 C. 렌쳐의 책 'Linear models in statistics'을 읽고 정리한 내용입니다. 2.1 행렬 및 벡터 표기법 2.1.1 Matrices, Vectors, and Scalars matrix, 행렬 행렬을 나타내기 위해 대문자 굵은 글씨를 사용하

벡터들을 포함하는 집합 S가 다음을 만족할 때 이를 벡터 공간(vector space)라고 한다. (ⅰ) O ∈ S (ⅱ) x ∈ S, y ∈ S 이면 x+y ∈ S. (closed for addition) (ⅲ) x ∈ S 이면, 임의의 실수 α에

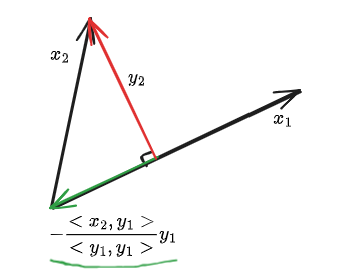
벡터 공간 S에 있는 벡터의 집합 ${x_1,x_2,\\dots,x_n}$에 대하여 다음을 만족하면 ${x_1,x_2,\\dots,x_n}$은 S의 기저(basis)이다. 1\. ${x_1,x_2,\\dots,x_n}$ spans the vector space S.2\

1. 열공간(column space)과 행공간(row space) $m\times n$ 행렬 $A$ n개의 열벡터에 의해 생성되는 $\mathbb{R}^m$의 부분 공간을 A의 열공간(column space)이라고 한다. m개의 행벡터에 의해 생성되는 $\mathbb