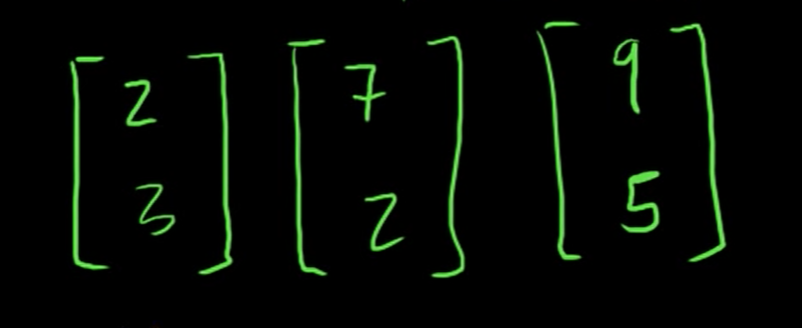Linear dependence and independence

Ex 1

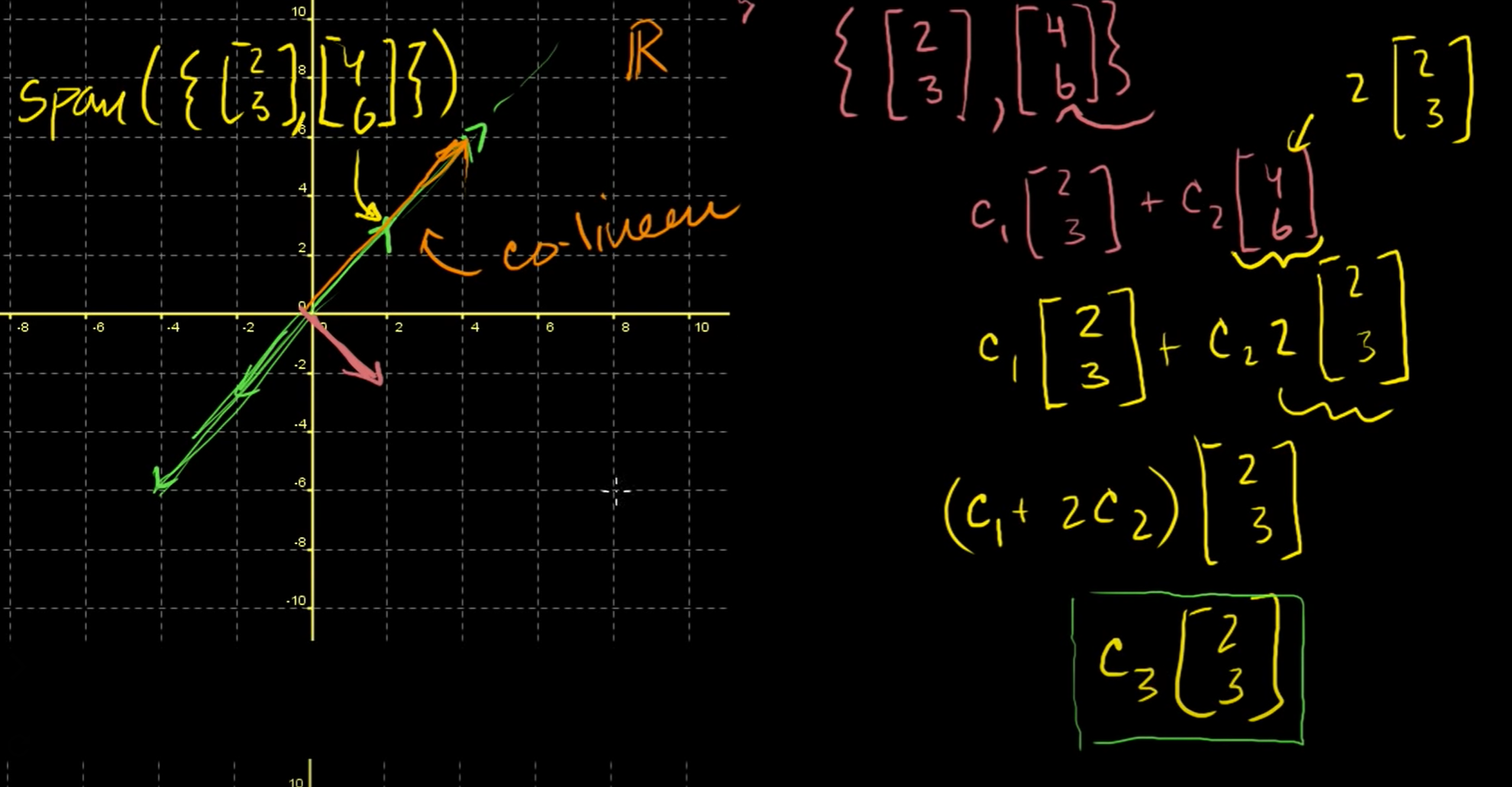
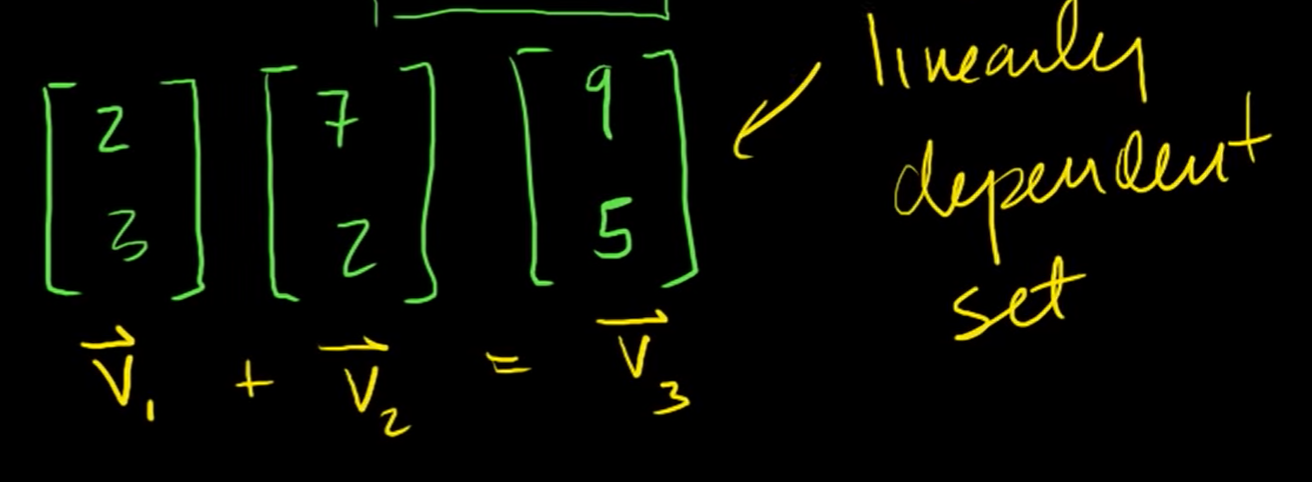
We call this set linearly dependent set. Linearly dependent means that one of the vector in the set can be represented by some combination of the other vectors in the set. Whichever vector you pick that can be represented by the others, it's not adding any new directionaility or any new information!

Ex 2

❓ Are these linearly independent?

❗ nope! $\vec {v_3}$ is a linear combinations of these other two vectors!

• span( $\vec {v_1}$,$\vec {v_2}$ ,$\vec {v_3}$ ) = span( $\vec {v_1}$,$\vec {v_2}$ ) = $R^2$

Ex 3

These are linearly independent!

More on linear independence

Let's say there is a linearly dependent set $S = {(\vec {v_1}, \vec {v_2}, ..., \vec {v_n})}$.

Linearly dependent $\iff$ ($c_1 \cdot \vec{v_1} + c_2 \cdot \vec{v_2} + ... + c_n \cdot \vec{v_n}) = \vec{0}$ $for \space some \space c_i \space is \space not \space all \space zero.$

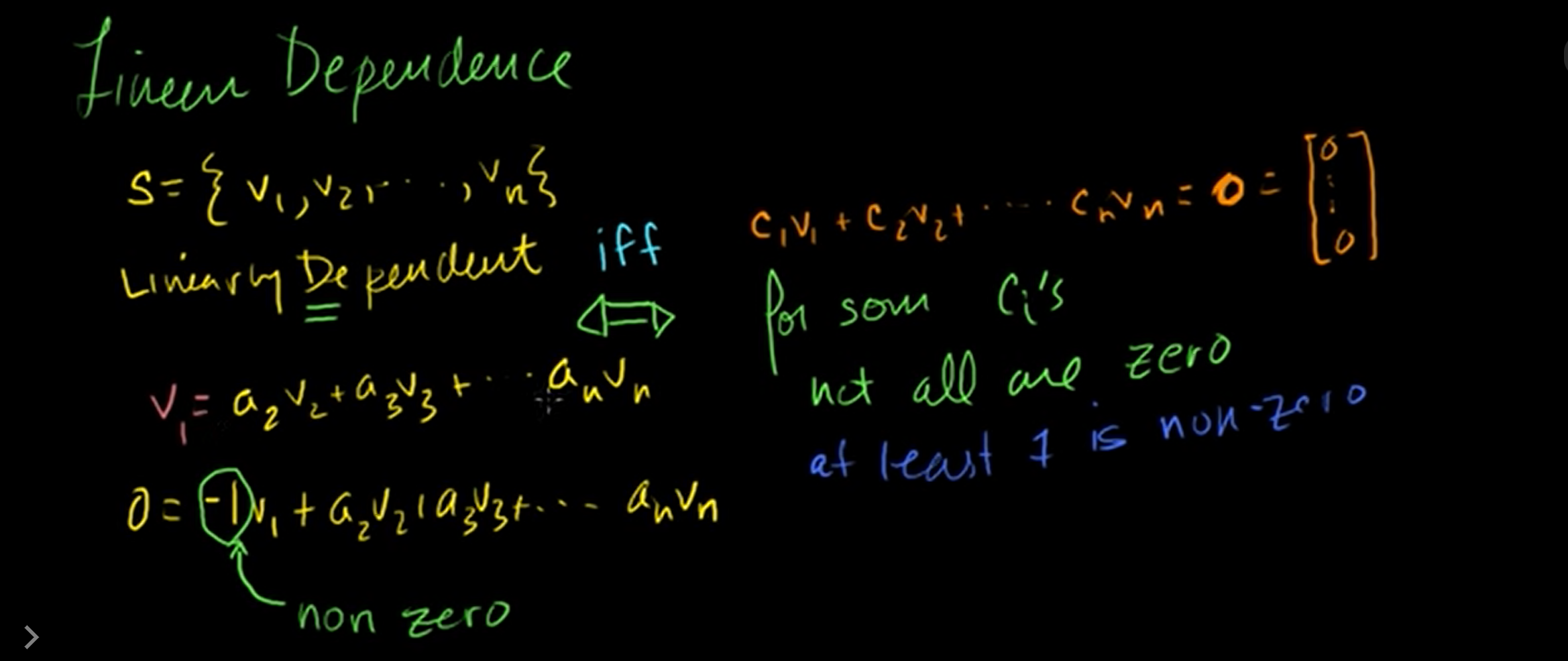
Now let's prove this proposition. we should show a vector $\vec {v_1}$ can be represented by other vectors' linear combination.

Proof 1)

Proof 2)

Span and linear independence example

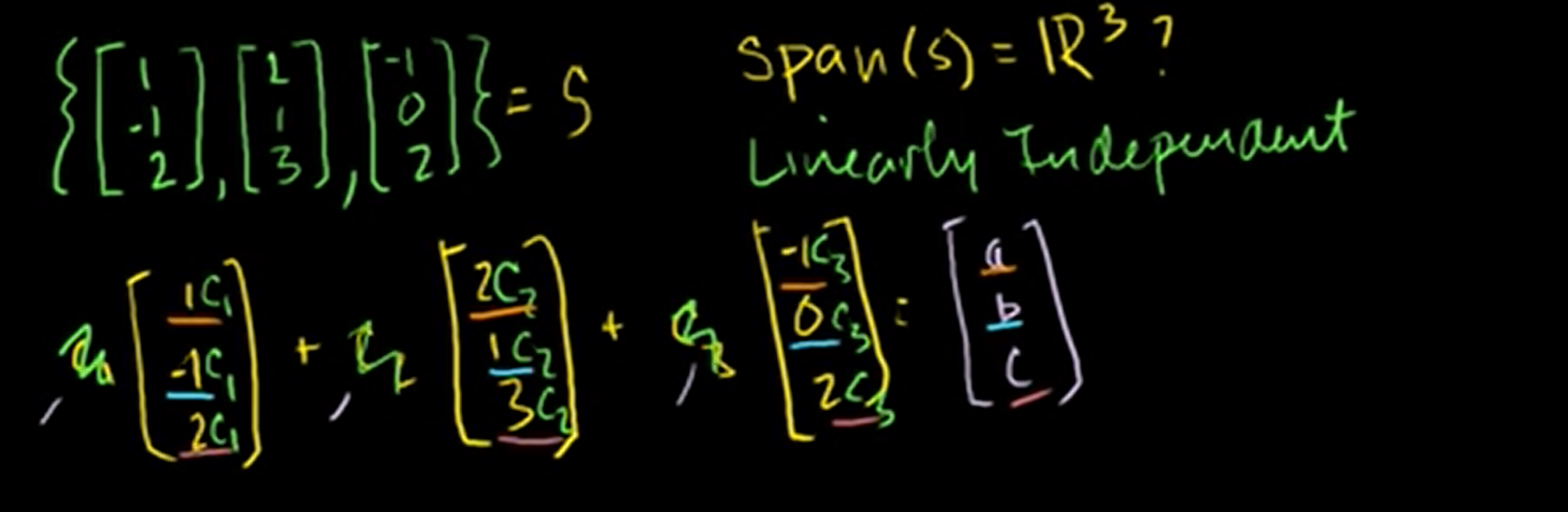
Let's see an example if $span(s)$ is $\mathbb R^3$.

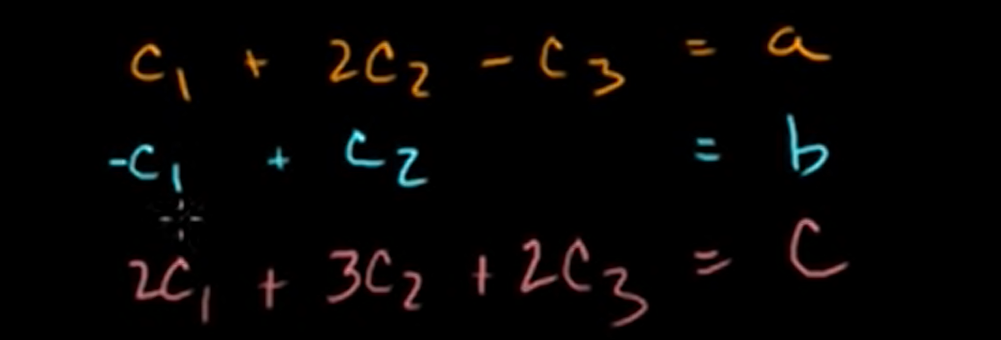
Using these equations, we can calculate like this.

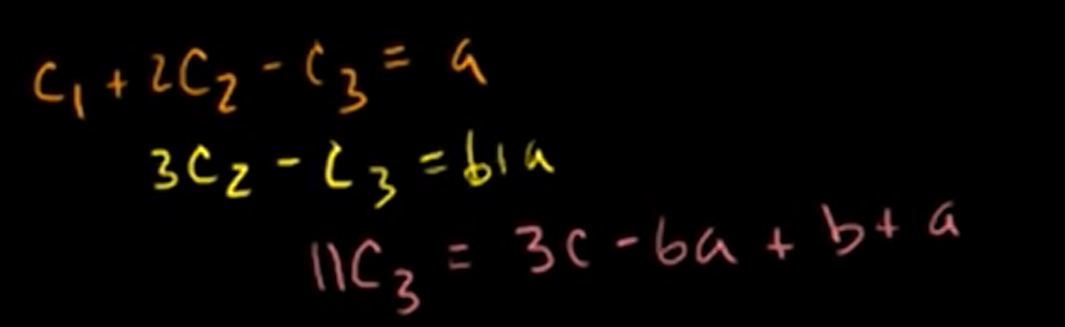
And from these equations, we can make equations about ${c_1}, {c_2}, {c_3}$.

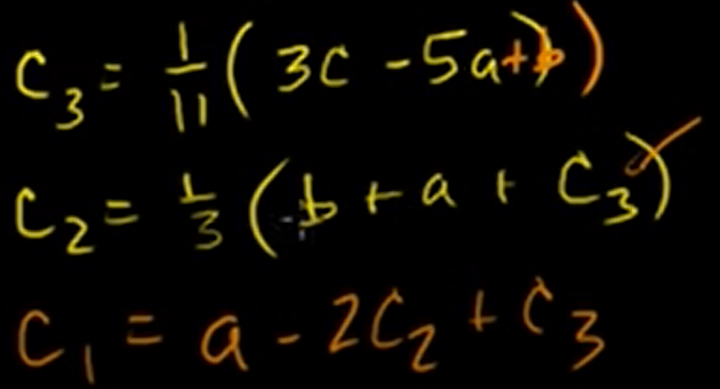
Span

It means that, If we get any vector $\left[ \begin{matrix} a \\ b \\ c \end{matrix} \right]$ $in \space R^3$, we can always find ${c_1}, {c_2}, {c_3}$ and represent the vector!

Linearly Independent

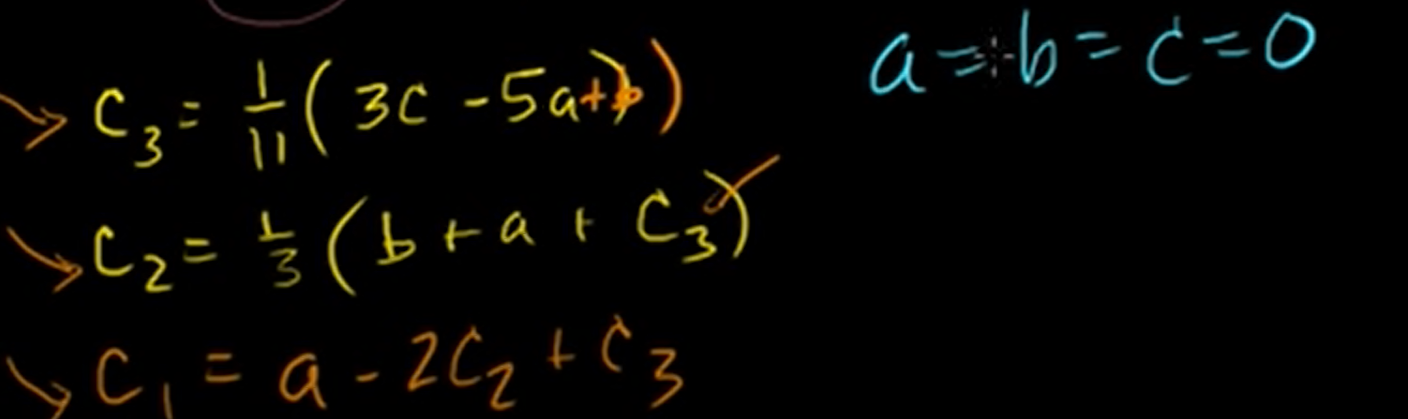
Linearly independent $\iff$ We cannot find the solution which satisfies ($c_1 \cdot \vec{v_1} + c_2 \cdot \vec{v_2} + ... + c_n \cdot \vec{v_n}) = \vec{0} \space$ except every $c$ is zero.

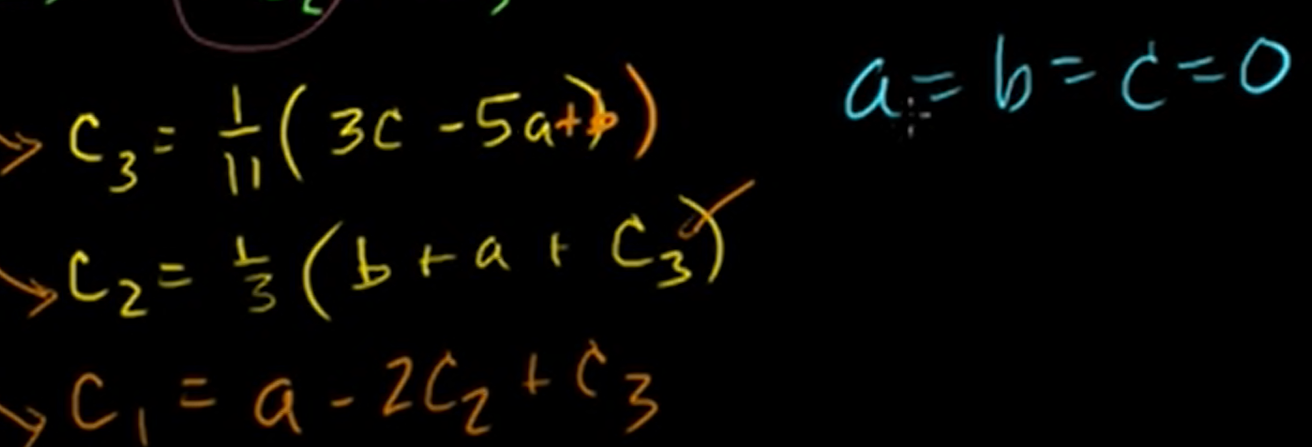
So if a,b,c are zero, c1,c2,c3 should be zero, too.
And none of these vectors can be represented as a combination of the other two.