Lab 7-1: Tips

목차

• Reminder: Maximum likelihood Estimation
• Reminder: Optimization via Gradient Descent
• Reminder: Overfitting and Regularization
• Training and Test Datset
• Learning Rate
• Date Preprocessing

Maximum likelihood Estimation(MLE)

Maximum likelihood Estimation에 대해 자세히 알아봅시다. 왜 이걸 하는지 또한 살펴봅시다.

압정이 떨어질 때 바늘이 하늘을 향할지, 그 외 결과가 나올지에 대해 알아본다고 가정합시다. 두 가지 경우 같이 없으므로 Bernoulli Distribution이 된다. 이를 여러 번 던지게 되면 Binary distribution이 된다.

Binary Distribution을 봅시다.

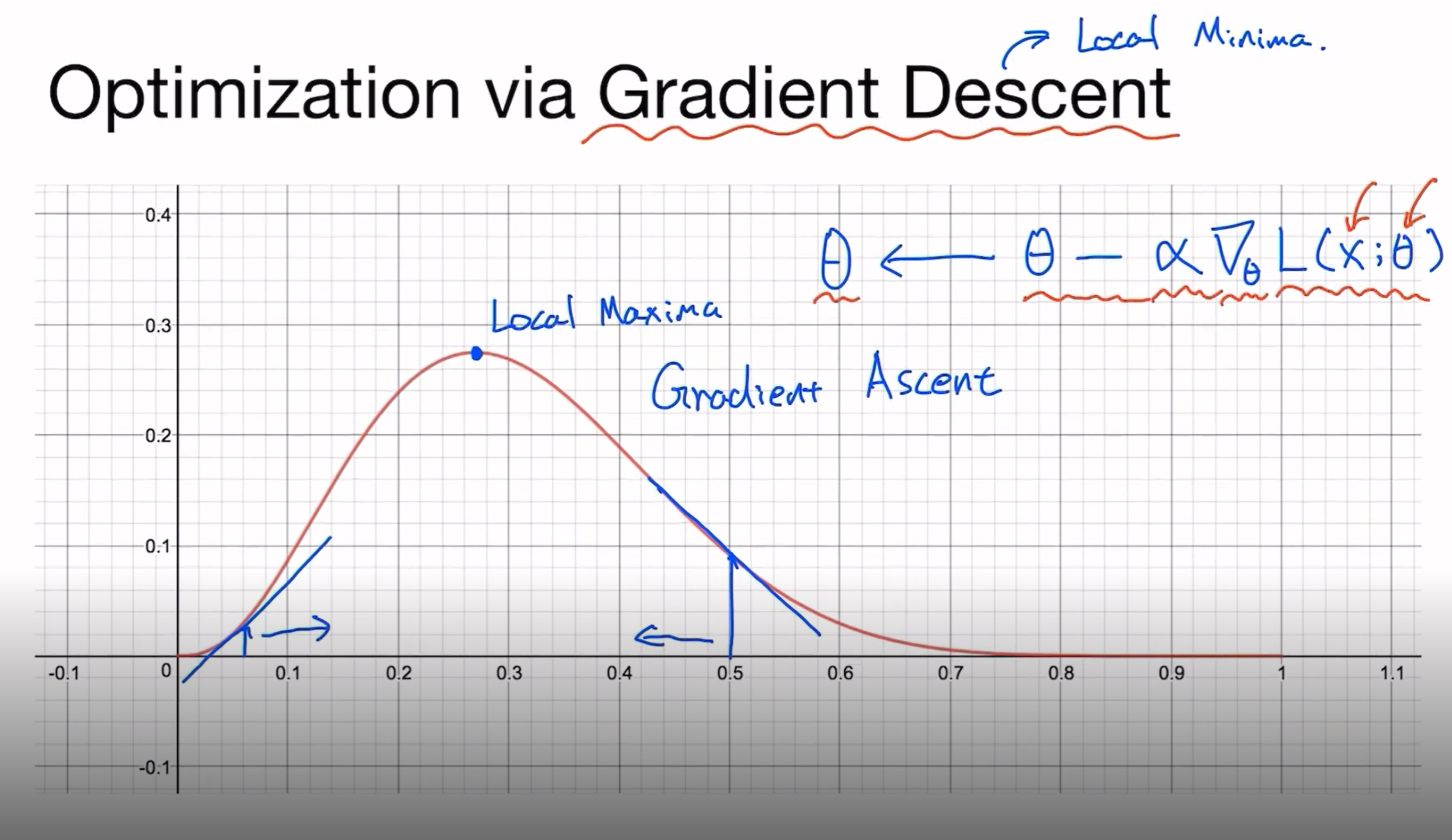
이 likelihood가 maximize 되는 부분을 살펴보자. 우리가 관찰한 데이터을 가장 잘 설명하는 확률 분포 함수의 파라미터(theta)를 찾는 과정을 MLE라고 부릅니다.

그래서 우리는 이를 어떻게 할까요?? 바로 그 기울기를 구하면 됩니다.

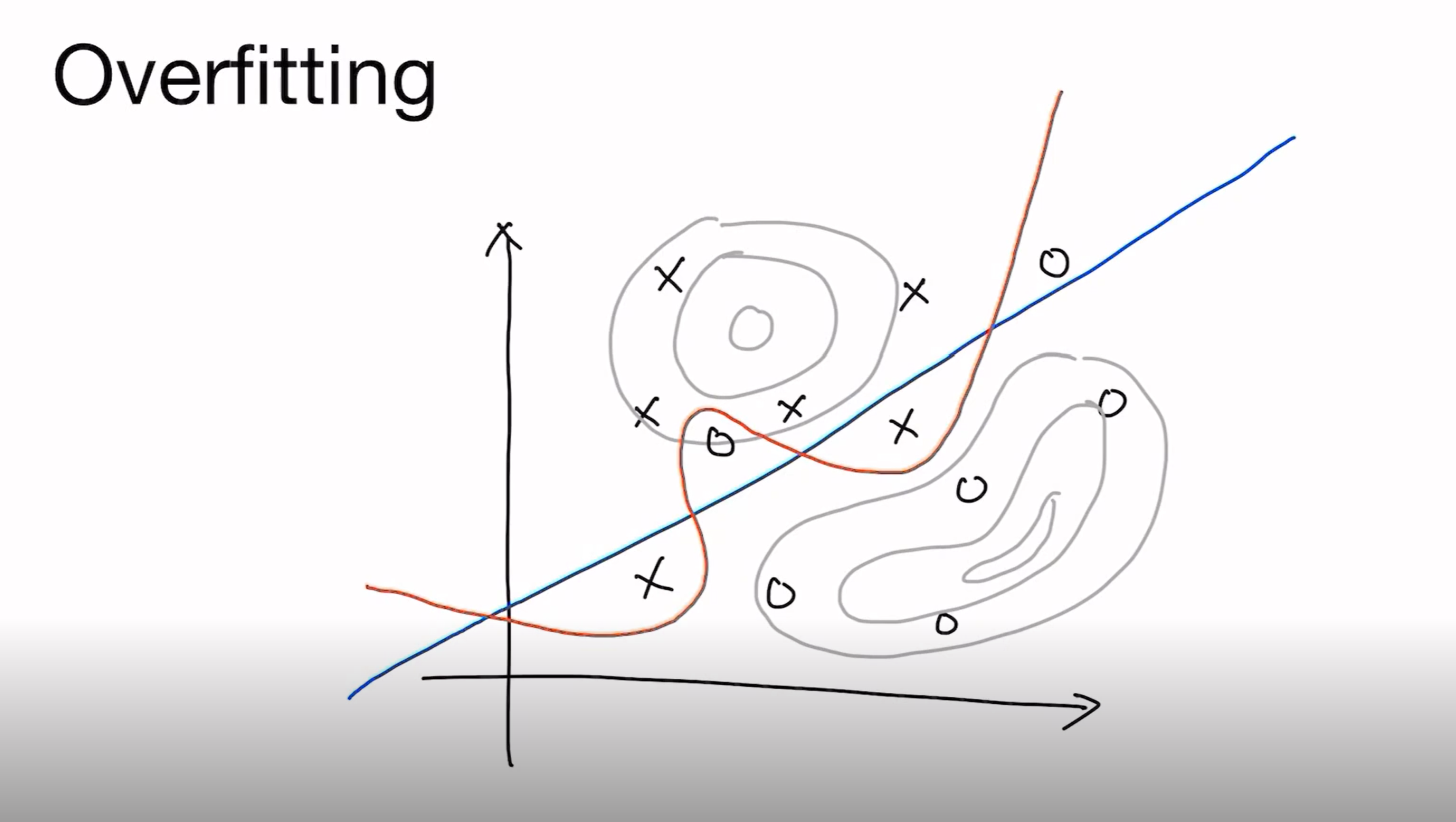
하지만 이 MLE같은 경우는 overfitting이라는 숙명을 거치게 됩니다. 이렇게 우리가 알고 싶은만큼이 아니라, 주어진 데이터에만 작동하게 과도하게 fitting 되어버린 케이스, 상황을 overfitting이라고 부릅니다.

이 overfitting을 어떻게 최소화 할 수 있을까요?

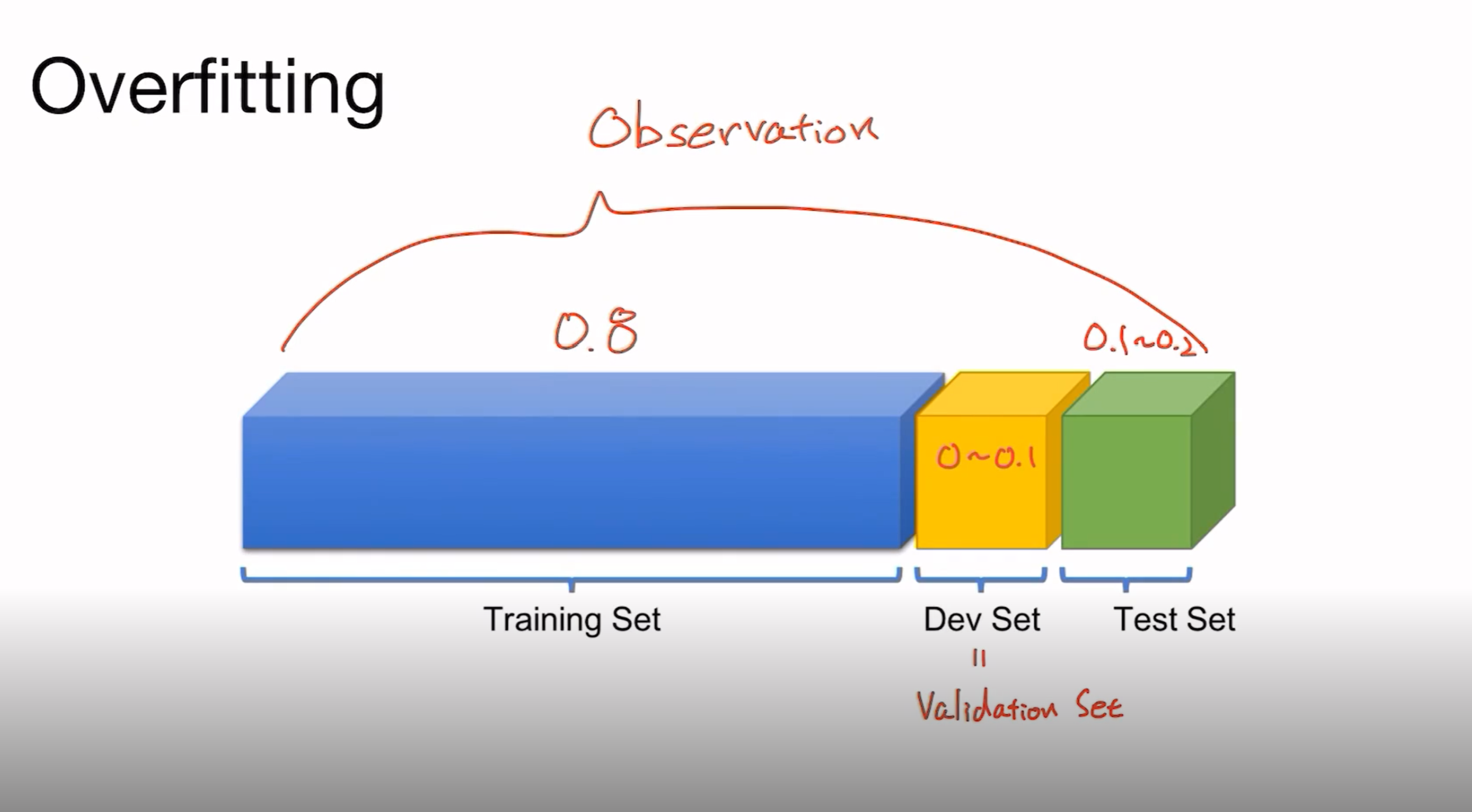
데이터를 Training set, Development set, Test set으로 나눠서 해당 훈련이 얼마나 잘 학습된지를 검증하면 됩니다.

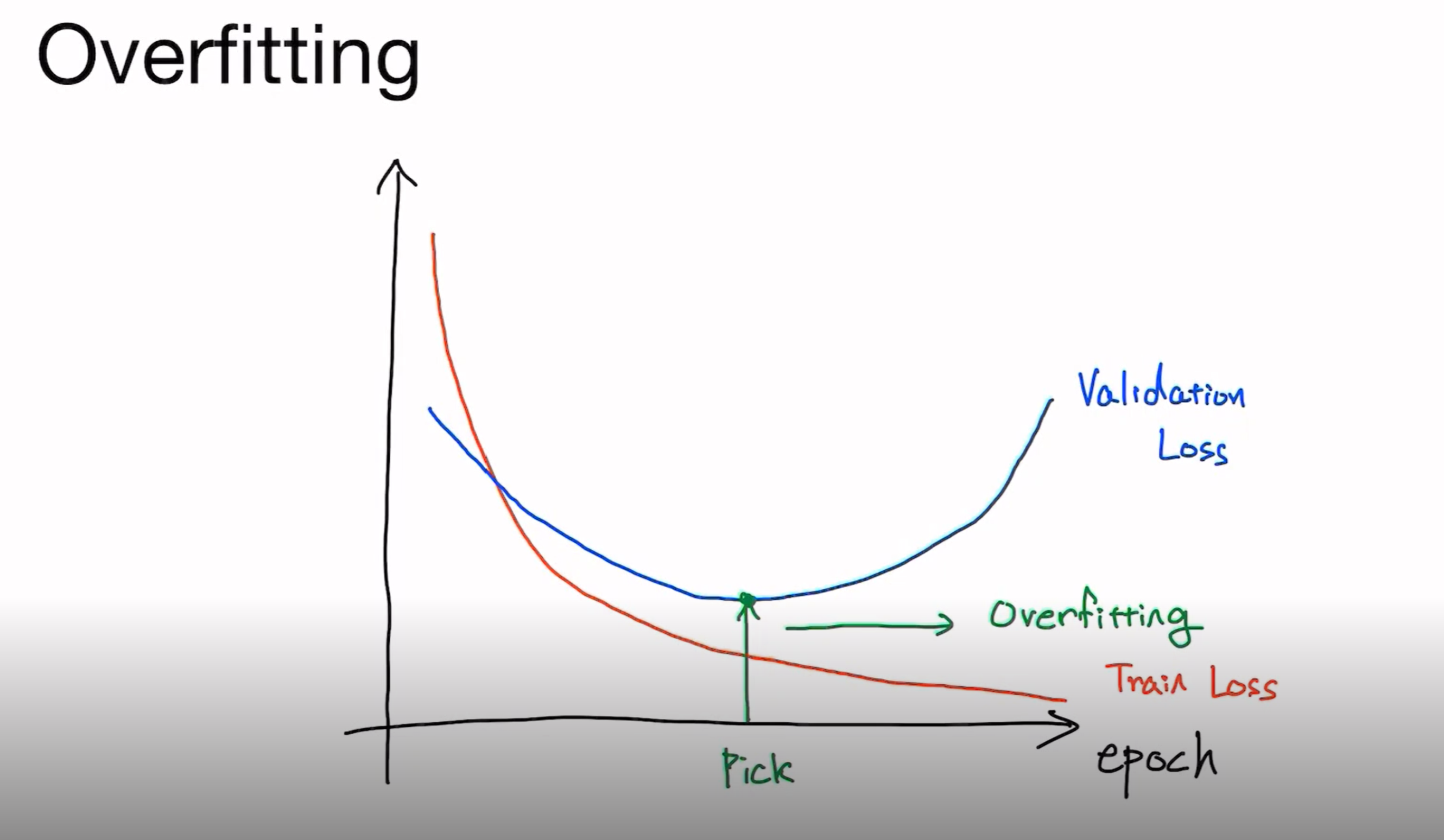
이렇게 Validation set의 loss가 증가하는 부분에서 Early stopping을 하여 overfitting을 방지하면 됩니다.

추가로 overfitting을 막는 방법은 무엇이 있을까요??
첫 번째는 데이터를 많이 모으는 것입니다. 편향된 데이터가 미치는 영향을 줄일 가능성이 큽니다.
두 번째는 feature의 숫자를 줄이는 법입니다.
마지막은 Regularization을 실행하는 것입니다.

Regularization에는 다음과 같이 여러 가지 방법이 있습니다. 딥러닝의 경우, Network Size를 줄이는 것도 좋은 방법이 될 것입니다.

가장 많이 쓰이는 방법은 Dropout, Batch Normalization이 되겠습니다. 이들 또한 딥러닝에 한해서입니다. 추후에 다룰 예정입니다.

그래서 추후에 DNN을 훈련시킬 때는 다음과 같은 과정을 따를 것입니다.

이제 실습을 해 봅시다.

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# For reproducibility
torch.manual_seed(1)

<torch._C.Generator at 0x7f0ddfd479b0>

Training and Test Datasets

# x_train = (m, 3)
# y_train = (m, )
x_train = torch.FloatTensor([[1, 2, 1],
                             [1, 3, 2],
                             [1, 3, 4],
                             [1, 5, 5],
                             [1, 7, 5],
                             [1, 2, 5],
                             [1, 6, 6],
                             [1, 7, 7]
                            ])
y_train = torch.LongTensor([2, 2, 2, 1, 1, 1, 0, 0])

# x_test = (m', 3)
# y_test = (m', )

x_test = torch.FloatTensor([[2, 1, 1], [3, 1, 2], [3, 3, 4]])
y_test = torch.LongTensor([2, 2, 2])

Model

class SoftmaxClassifierModel(nn.Module): # nn.Module 상속 받은 후 선언
    def __init__(self): 
        super().__init__()
        self.linear = nn.Linear(3, 3)
    def forward(self, x):
        return self.linear(x) # x = (m, 3) -> (m, 3)

model = SoftmaxClassifierModel()

# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.1)

def train(model, optimizer, x_train, y_train):
    nb_epochs = 20
    for epoch in range(nb_epochs):

        # H(x) 계산
        prediction = model(x_train)

        # cost 계산
        cost = F.cross_entropy(prediction, y_train)

        # cost로 H(x) 개선
        optimizer.zero_grad()
        cost.backward()
        optimizer.step()

        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))

def test(model, optimizer, x_test, y_test):
    prediction = model(x_test)
    predicted_classes = prediction.max(1)[1]
    correct_count = (predicted_classes == y_test).sum().item()
    cost = F.cross_entropy(prediction, y_test)

    print('Accuracy: {}% Cost: {:.6f}'.format(
         correct_count / len(y_test) * 100, cost.item()
    ))

train(model, optimizer, x_train, y_train)

Epoch    0/20 Cost: 2.203667
Epoch    1/20 Cost: 1.199645
Epoch    2/20 Cost: 1.142985
Epoch    3/20 Cost: 1.117769
Epoch    4/20 Cost: 1.100901
Epoch    5/20 Cost: 1.089523
Epoch    6/20 Cost: 1.079872
Epoch    7/20 Cost: 1.071320
Epoch    8/20 Cost: 1.063325
Epoch    9/20 Cost: 1.055720
Epoch   10/20 Cost: 1.048378
Epoch   11/20 Cost: 1.041245
Epoch   12/20 Cost: 1.034285
Epoch   13/20 Cost: 1.027478
Epoch   14/20 Cost: 1.020813
Epoch   15/20 Cost: 1.014279
Epoch   16/20 Cost: 1.007872
Epoch   17/20 Cost: 1.001586
Epoch   18/20 Cost: 0.995419
Epoch   19/20 Cost: 0.989365

test(model, optimizer, x_test, y_test)

Accuracy: 0.0% Cost: 1.425844

Learning Rate

Gradient Descent 에서의 $\alpha$ 값

optimizer = optim.SGD(model.parameters(), lr=0.1) 에서 lr=0.1 이다

learning rate이 너무 크면 diverge 하면서 cost 가 점점 늘어난다 (overshooting).

model = SoftmaxClassifierModel()

optimizer = optim.SGD(model.parameters(), lr=1e5)

train(model, optimizer, x_train, y_train)

Epoch    0/20 Cost: 1.280268
Epoch    1/20 Cost: 976950.812500
Epoch    2/20 Cost: 1279135.125000
Epoch    3/20 Cost: 1198379.000000
Epoch    4/20 Cost: 1098825.875000
Epoch    5/20 Cost: 1968197.625000
Epoch    6/20 Cost: 284763.250000
Epoch    7/20 Cost: 1532260.125000
Epoch    8/20 Cost: 1651504.000000
Epoch    9/20 Cost: 521878.500000
Epoch   10/20 Cost: 1397263.250000
Epoch   11/20 Cost: 750986.250000
Epoch   12/20 Cost: 918691.500000
Epoch   13/20 Cost: 1487888.250000
Epoch   14/20 Cost: 1582260.125000
Epoch   15/20 Cost: 685818.062500
Epoch   16/20 Cost: 1140048.750000
Epoch   17/20 Cost: 940566.500000
Epoch   18/20 Cost: 931638.250000
Epoch   19/20 Cost: 1971322.625000

learning rate이 너무 작으면 cost가 거의 줄어들지 않는다.

model = SoftmaxClassifierModel()

optimizer = optim.SGD(model.parameters(), lr=1e-10)

train(model, optimizer, x_train, y_train)

Epoch    0/20 Cost: 3.187324
Epoch    1/20 Cost: 3.187324
Epoch    2/20 Cost: 3.187324
Epoch    3/20 Cost: 3.187324
Epoch    4/20 Cost: 3.187324
Epoch    5/20 Cost: 3.187324
Epoch    6/20 Cost: 3.187324
Epoch    7/20 Cost: 3.187324
Epoch    8/20 Cost: 3.187324
Epoch    9/20 Cost: 3.187324
Epoch   10/20 Cost: 3.187324
Epoch   11/20 Cost: 3.187324
Epoch   12/20 Cost: 3.187324
Epoch   13/20 Cost: 3.187324
Epoch   14/20 Cost: 3.187324
Epoch   15/20 Cost: 3.187324
Epoch   16/20 Cost: 3.187324
Epoch   17/20 Cost: 3.187324
Epoch   18/20 Cost: 3.187324
Epoch   19/20 Cost: 3.187324

적절한 숫자로 시작해 발산하면 작게, cost가 줄어들지 않으면 크게 조정하자.

model = SoftmaxClassifierModel()

optimizer = optim.SGD(model.parameters(), lr=1e-1)

train(model, optimizer, x_train, y_train)

Epoch    0/20 Cost: 1.341573
Epoch    1/20 Cost: 1.198802
Epoch    2/20 Cost: 1.150877
Epoch    3/20 Cost: 1.131977
Epoch    4/20 Cost: 1.116242
Epoch    5/20 Cost: 1.102514
Epoch    6/20 Cost: 1.089676
Epoch    7/20 Cost: 1.077479
Epoch    8/20 Cost: 1.065775
Epoch    9/20 Cost: 1.054511
Epoch   10/20 Cost: 1.043655
Epoch   11/20 Cost: 1.033187
Epoch   12/20 Cost: 1.023091
Epoch   13/20 Cost: 1.013356
Epoch   14/20 Cost: 1.003968
Epoch   15/20 Cost: 0.994917
Epoch   16/20 Cost: 0.986189
Epoch   17/20 Cost: 0.977775
Epoch   18/20 Cost: 0.969660
Epoch   19/20 Cost: 0.961836

Data Preprocessing (데이터 전처리)

데이터를 zero-center하고 normalize하자.

x_train = torch.FloatTensor([[73, 80, 75],
                             [93, 88, 93],
                             [89, 91, 90],
                             [96, 98, 100],
                             [73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])

$x'_j = \frac{x_j - \mu_j}{\sigma_j}$

여기서 $\sigma$ 는 standard deviation, $\mu$ 는 평균값 이다.

mu = x_train.mean(dim=0)

sigma = x_train.std(dim=0)

norm_x_train = (x_train - mu) / sigma

print(norm_x_train)

tensor([[-1.0674, -0.3758, -0.8398],
        [ 0.7418,  0.2778,  0.5863],
        [ 0.3799,  0.5229,  0.3486],
        [ 1.0132,  1.0948,  1.1409],
        [-1.0674, -1.5197, -1.2360]])

Normalize와 zero center한 X로 학습해서 성능을 보자

class MultivariateLinearRegressionModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(3, 1)

    def forward(self, x):
        return self.linear(x)

model = MultivariateLinearRegressionModel()

optimizer = optim.SGD(model.parameters(), lr=1e-1)

def train(model, optimizer, x_train, y_train):
    nb_epochs = 20
    for epoch in range(nb_epochs):

        # H(x) 계산
        prediction = model(x_train)

        # cost 계산
        cost = F.mse_loss(prediction, y_train)

        # cost로 H(x) 개선
        optimizer.zero_grad()
        cost.backward()
        optimizer.step()

        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))

train(model, optimizer, norm_x_train, y_train)

Epoch    0/20 Cost: 29785.091797
Epoch    1/20 Cost: 18906.164062
Epoch    2/20 Cost: 12054.674805
Epoch    3/20 Cost: 7702.029297
Epoch    4/20 Cost: 4925.733398
Epoch    5/20 Cost: 3151.632568
Epoch    6/20 Cost: 2016.996094
Epoch    7/20 Cost: 1291.051270
Epoch    8/20 Cost: 826.505310
Epoch    9/20 Cost: 529.207336
Epoch   10/20 Cost: 338.934204
Epoch   11/20 Cost: 217.153549
Epoch   12/20 Cost: 139.206741
Epoch   13/20 Cost: 89.313782
Epoch   14/20 Cost: 57.375462
Epoch   15/20 Cost: 36.928429
Epoch   16/20 Cost: 23.835772
Epoch   17/20 Cost: 15.450428
Epoch   18/20 Cost: 10.077808
Epoch   19/20 Cost: 6.633700

Overfitting

너무 학습 데이터에 한해 잘 학습해 테스트 데이터에 좋은 성능을 내지 못할 수도 있다.

이것을 방지하는 방법은 크게 세 가지인데:

1. 더 많은 학습 데이터
2. 더 적은 양의 feature
3. Regularization

Regularization: Let's not have too big numbers in the weights

def train_with_regularization(model, optimizer, x_train, y_train):
    nb_epochs = 20
    for epoch in range(nb_epochs):

        # H(x) 계산
        prediction = model(x_train)

        # cost 계산
        cost = F.mse_loss(prediction, y_train)
        
        # l2 norm 계산
        l2_reg = 0
        for param in model.parameters():
            l2_reg += torch.norm(param)
            
        cost += l2_reg

        # cost로 H(x) 개선
        optimizer.zero_grad()
        cost.backward()
        optimizer.step()

        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch+1, nb_epochs, cost.item()
        ))

model = MultivariateLinearRegressionModel()

optimizer = optim.SGD(model.parameters(), lr=1e-1)

train_with_regularization(model, optimizer, norm_x_train, y_train)

Epoch    1/20 Cost: 29477.810547
Epoch    2/20 Cost: 18798.513672
Epoch    3/20 Cost: 12059.364258
Epoch    4/20 Cost: 7773.400879
Epoch    5/20 Cost: 5038.263672
Epoch    6/20 Cost: 3290.066406
Epoch    7/20 Cost: 2171.882568
Epoch    8/20 Cost: 1456.434570
Epoch    9/20 Cost: 998.598267
Epoch   10/20 Cost: 705.595398
Epoch   11/20 Cost: 518.073608
Epoch   12/20 Cost: 398.057220
Epoch   13/20 Cost: 321.242920
Epoch   14/20 Cost: 272.078247
Epoch   15/20 Cost: 240.609131
Epoch   16/20 Cost: 220.465637
Epoch   17/20 Cost: 207.570602
Epoch   18/20 Cost: 199.314804
Epoch   19/20 Cost: 194.028214
Epoch   20/20 Cost: 190.642014