Introduction
먼저 DNN의 문제점에 대해 분석하고 시작한다. Non-linear로 구성되어 있기 때문에, input, output 간의 복잡한 관계를 학습할 수 있다. 하지만 이렇게 복잡한 구조를 갖는 모델은 overfitting문제에 빠지기 쉽다.
지금까지의 모델들은 overfitting 문제에 빠지지 않기 위해서 해결책으로 validation dataset을 활용해 early stopping을 하거나 , 가중치에 패털티를 부과하는 L1,L2 regularization 사용했다.
여기 논문에서는 만약 computation을 무제한 할 수 있다면, 그림처럼 postrior probabilty를 활용해서 즉, 개별 세팅에 대해 파라미터와 웨이팅을 전부 계산해서 prediction하면 정확도가 늘 것이라고 했다. 라하지만 현실적으로 불가하다고 한다.
❔ posterior probabilty
❕ 알아보기
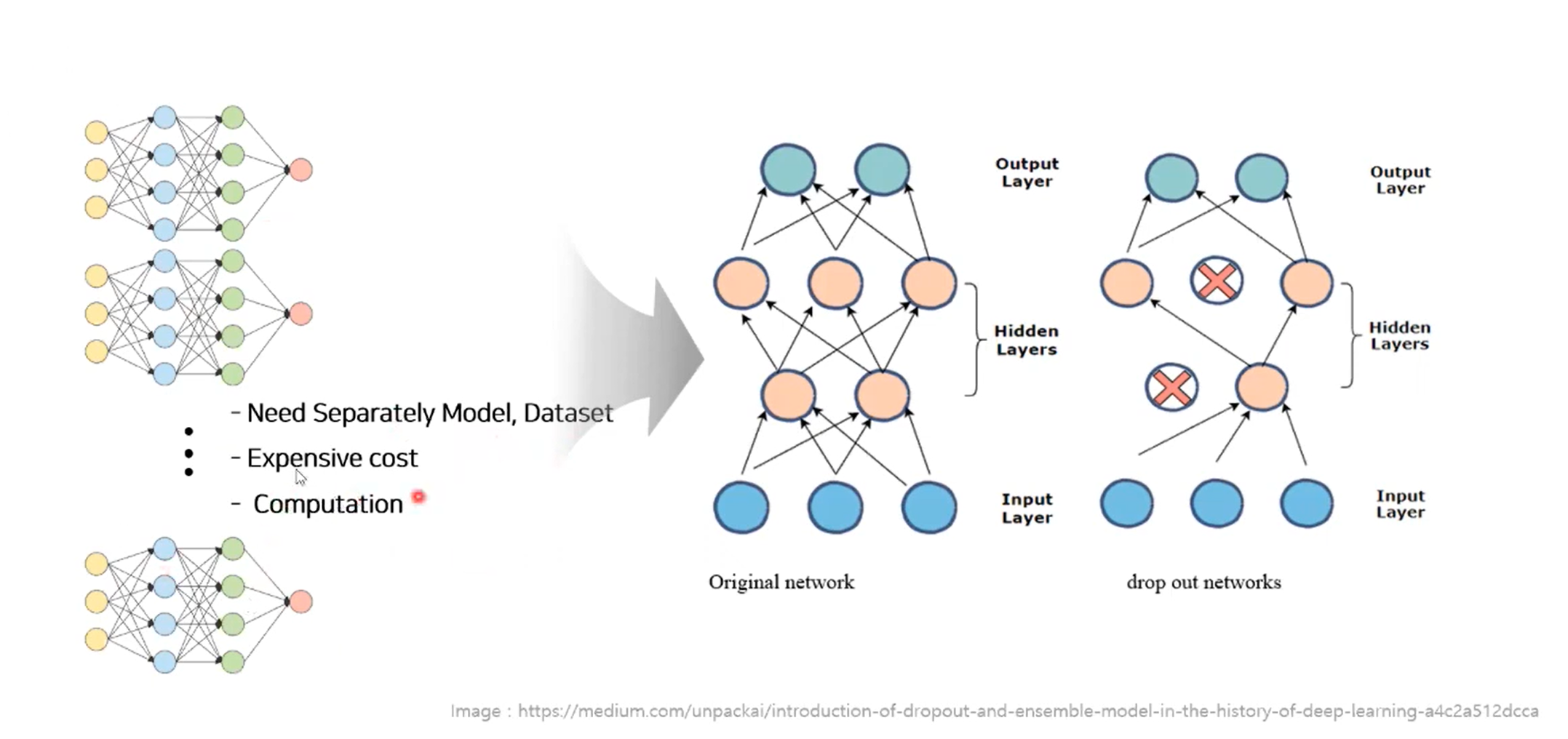
일반적으로 머신러닝의 경우 모델 결합을 통해, 앙상블 효과를 얻기 위해서는 서로 다른 모델과 데이터셋이 필요히다. 또한 computation 시간이 많이 필요하기 때문에 특정 application에서 response가 바로 필요한 상황에서는 사용을 할 수 없다.
그래서 이 논문에서는 이러한 문제점을 해결하기 위해 드랍아웃 제안하였다. 드랍아웃은 오버피팅을 방지하고 많은 수의 Neural Network를 효과적으로 분사하는 방법을 제시한다.
우측의 이미지와 같이, 랜덤의 확률 p값에 따라 노드를 제거하여 일시적으로 제거하는 기법을 말한다.
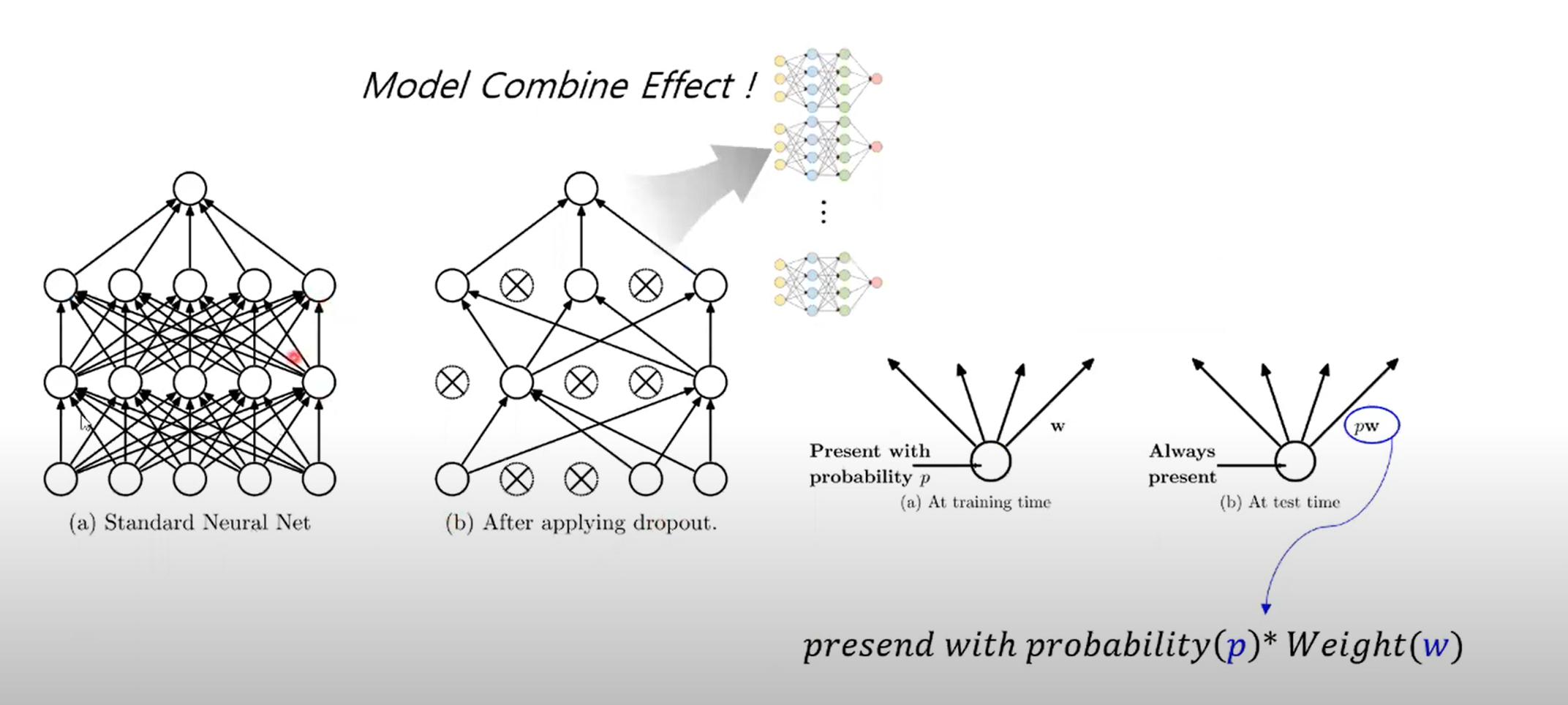
dropout을 통해 네트워크를 구성하게 되면 thinned한 네트워크를 구성하게 된다.
일부 유닛이 제거되는지에 따라 다양한 조합이 생긴다. 이렇게 다양한 모델이 생성되는 만큼, 다양한 모델을 얻을 수 있다. 그래서 다양한 모델이 결합되는 효과를 얻을 수 있다.
오른쪽 그림처럼, 어떤 노드는 학습이 되고 어떤 노드는 학습이 안 된다. 하지만 test를 할 때는 dropout이 수행되지 않는 일반적인 network에서 dropout이 될 확률 p값에 가중치 w를 곱한 형태도 값을 계산한다.
Motivation
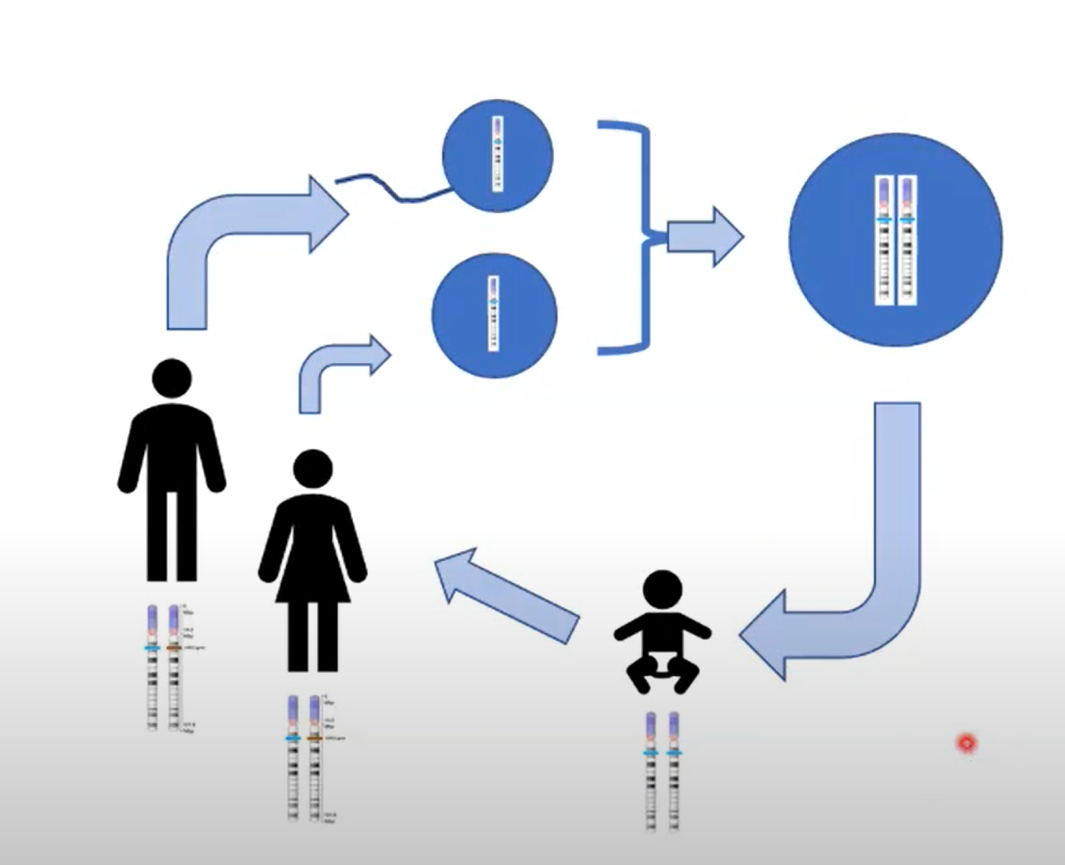
생식이론에서 고안했다고 한다.
무성생식보다 유성생식이 조금 더 유리할 수 있다는 생각을 하였다. (Random mutation!)
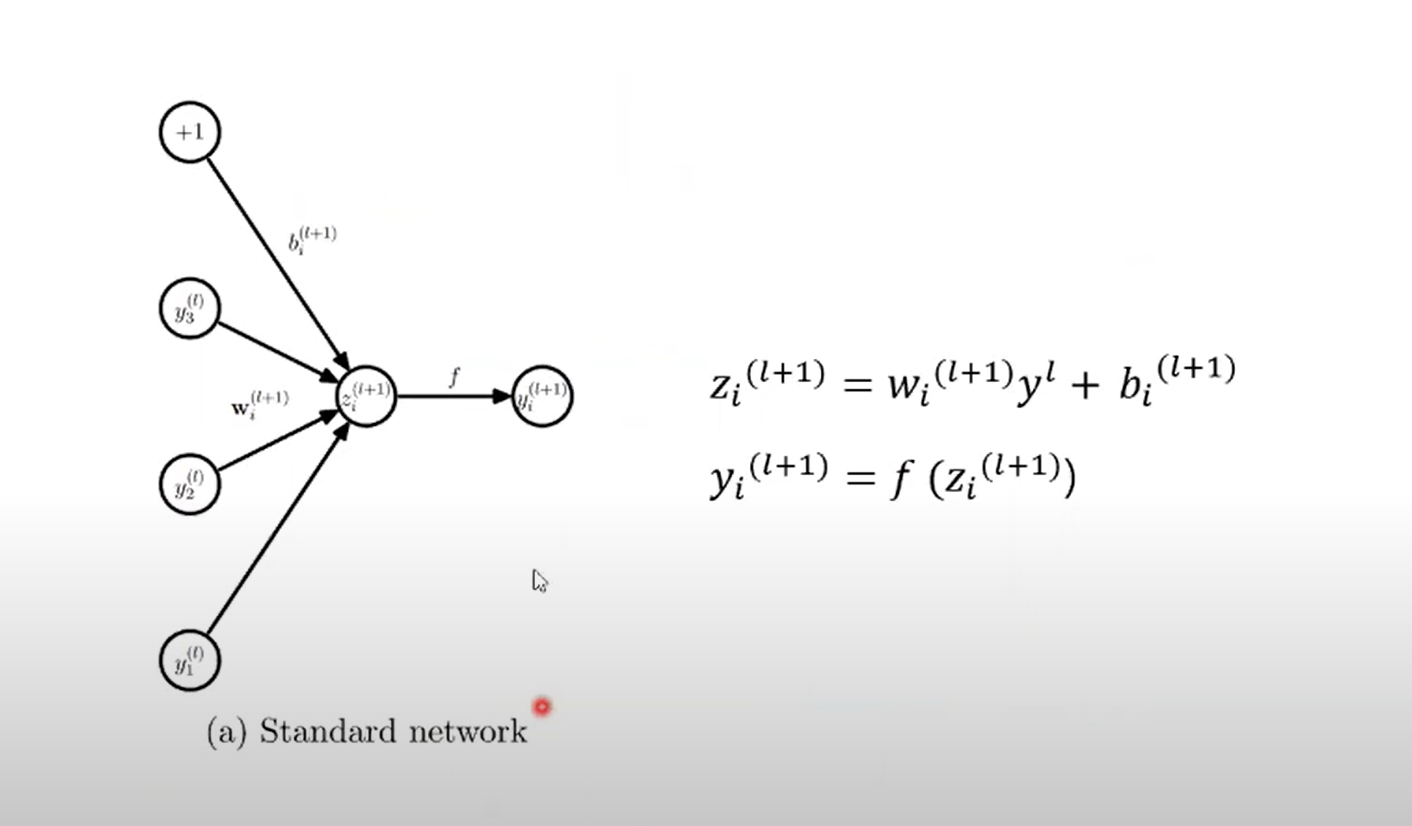
일반적인 모델 구조를 간단히 살펴보자. 가중치와 이전 시점의 값, bias로 표현한다. 이후 activation function을 지나 output 값이 나올 것이다.
Model Description
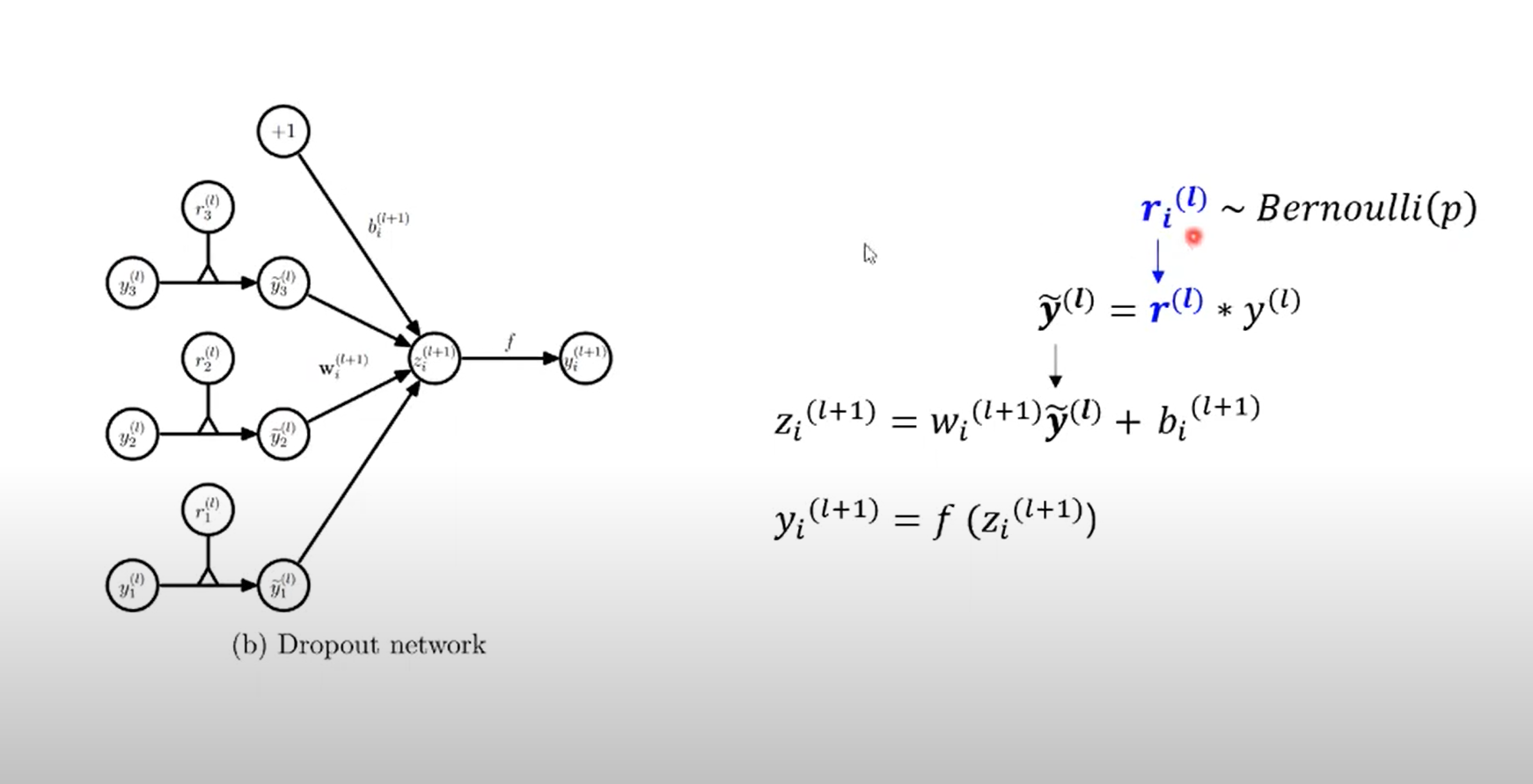
unit이 drop될 확률과 그렇지 않을 확률을 포함하기 때문에, 베르누이 분포를 따르게 되었고, 베르누이 분포를 따르는 r값만 더해주면 standard 모델 구조와 동일한 모델 가진다.
즉, unit의 포함여부에 베르누이 값을 더한 것이다.
Learning Dropout Nets
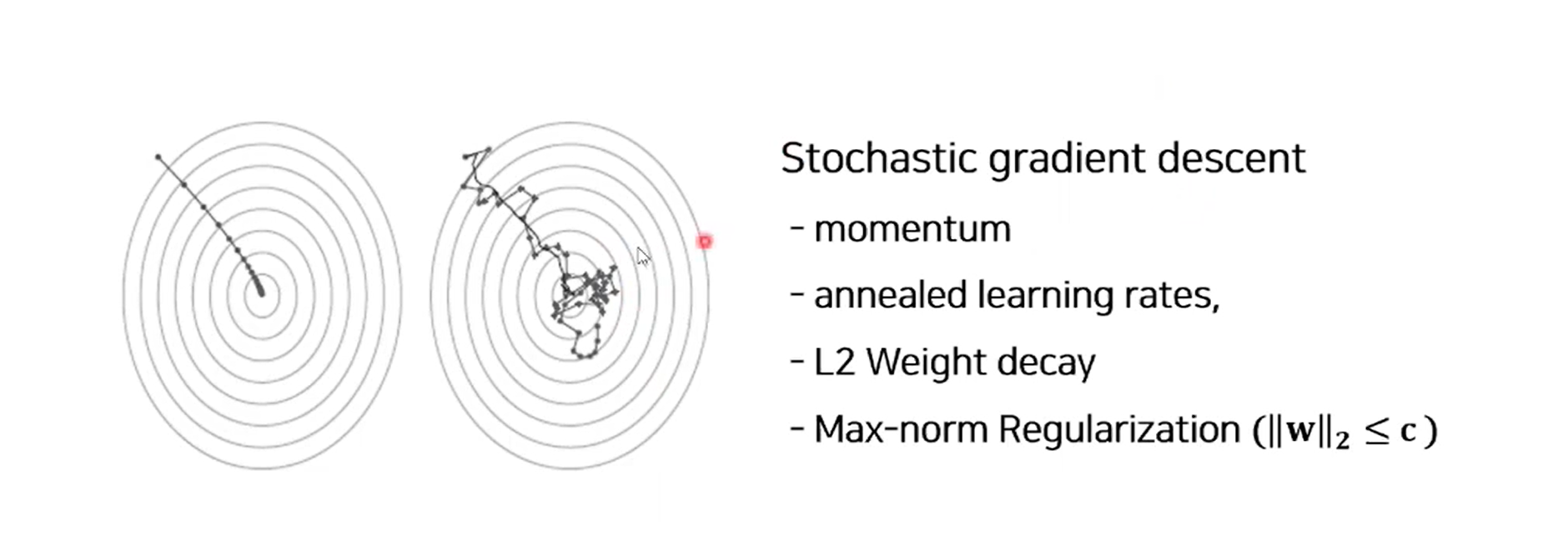
학습 방법은 일반적인 것과 동일하게 SGD 방법을 사용했다.
차이점이라하면 미니배치를 통해 케이스/유닛별로 드랍아웃을 진행했다.
또한 weight의 norm2값이 c보다 작다는 제약조건을 가지면 max-norm regularization 진행
❔ max-norm regularizatoin이란
❕
Experimental Result
모델은 간단하기 때문에 넘기고, 결과를 주로 보자.
MNIST
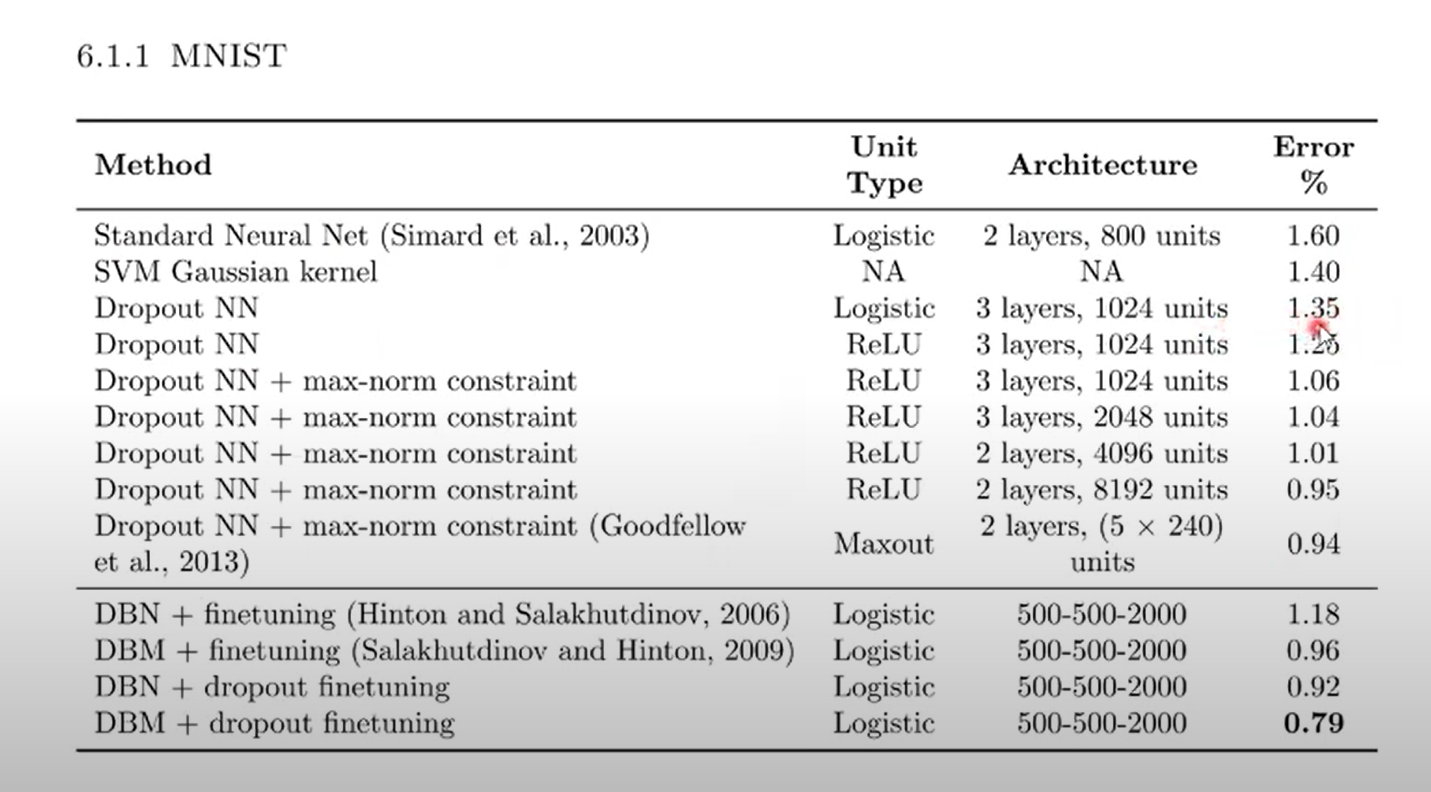
- ReLU 사용했을 때 Error 감소
- Max-norm 사용할 때 Error 감소
- 모델 사이즈 증가할수록 Error 감소
- DBM 모델에서도 잘 작동하는 거 보임
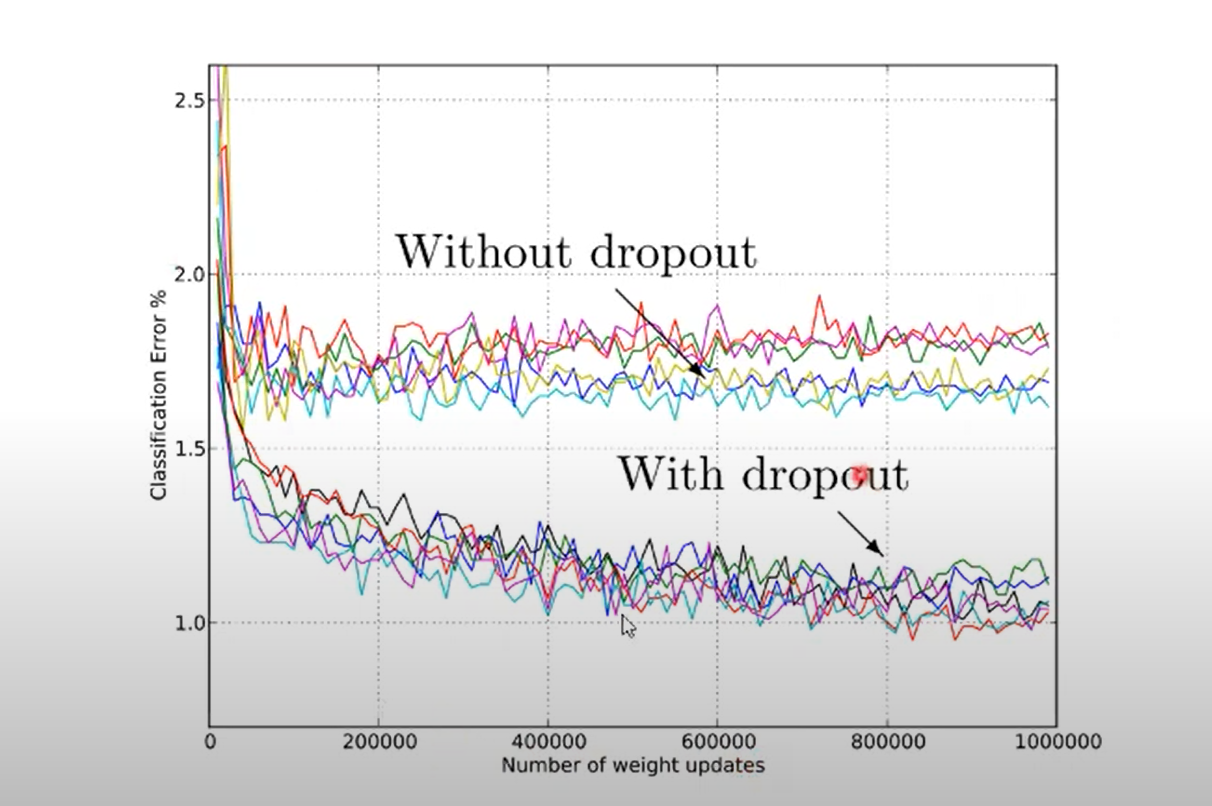
- 확률 p가 고정되었을 때 효과적으로 에러가 감소함을 확인
Street View House Numbers

- Dropout, Maxout 사용했을 때 감소
ImageNet

Results on TIMIT: 음성 데이터
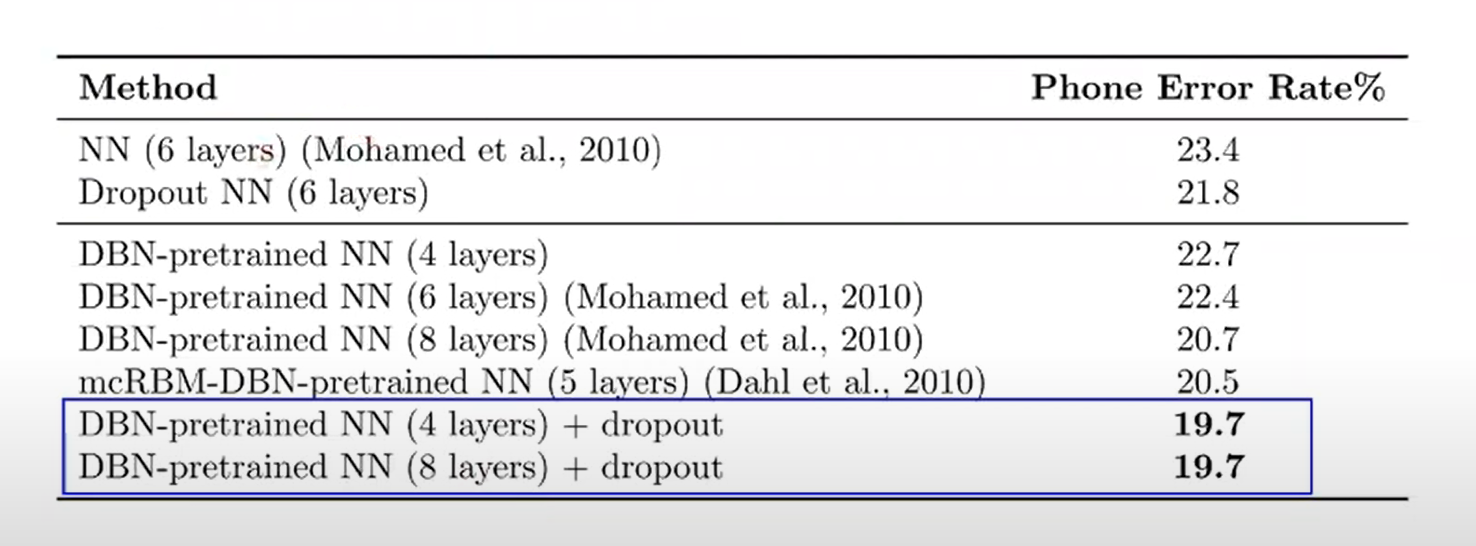
- 음성데이터에도 잘 적용됨
Comparison with Bayesian Neural Networks
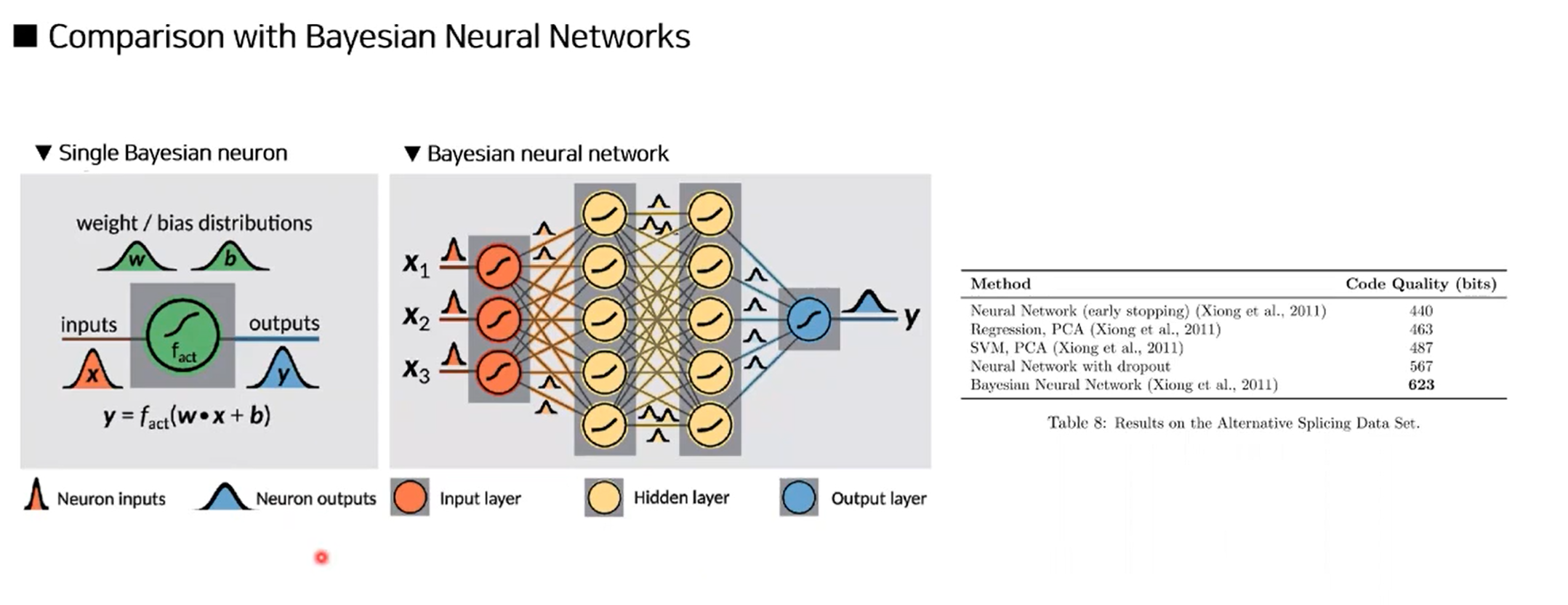
Salient Feature

MNIST를 오토인코더로 학습한 그림이다.
- Dropout을 사용할 때 더 선명한 특징이 보인다.
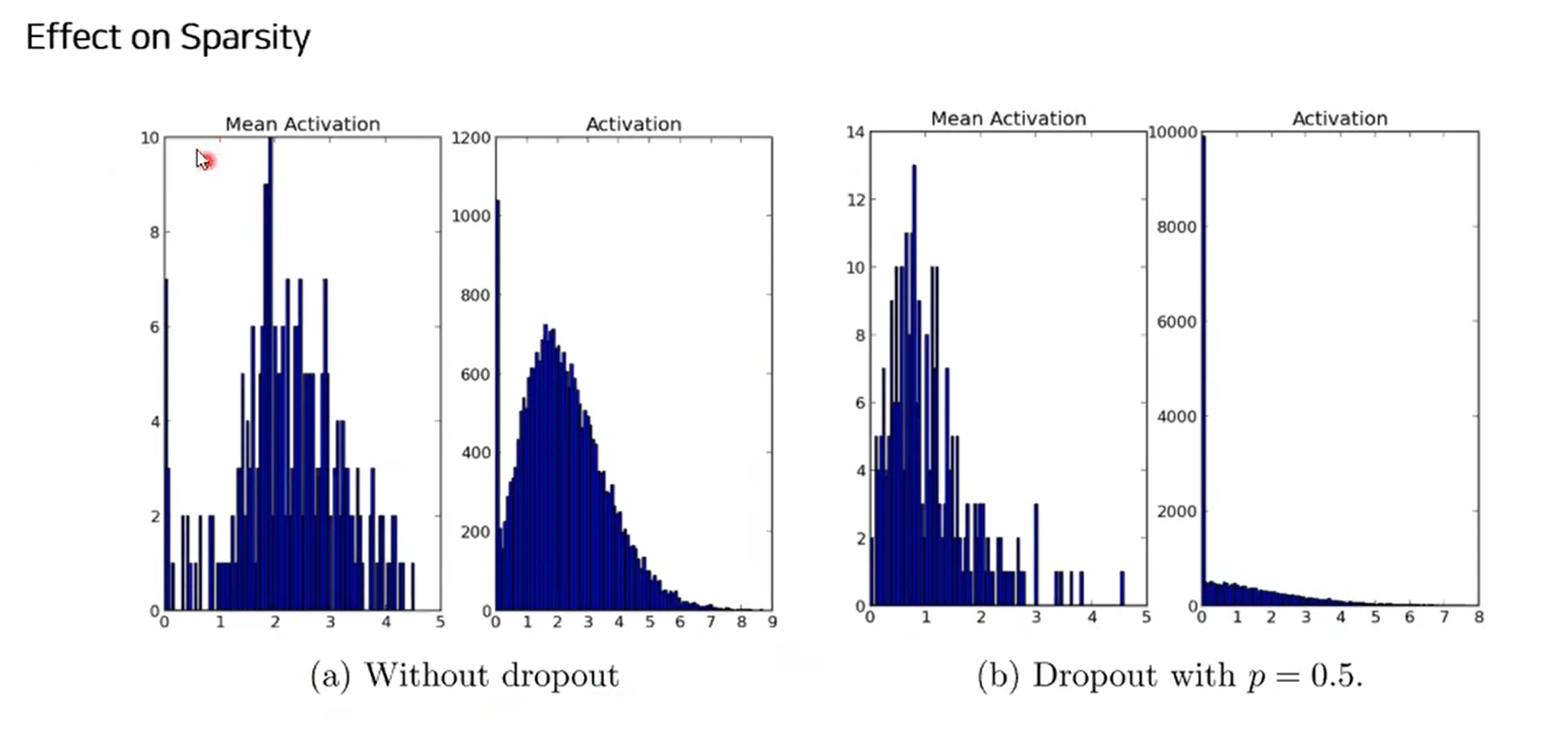
- side effect: activation이 sparsity한 경향이 있다.
퍼센트에 따른 성능
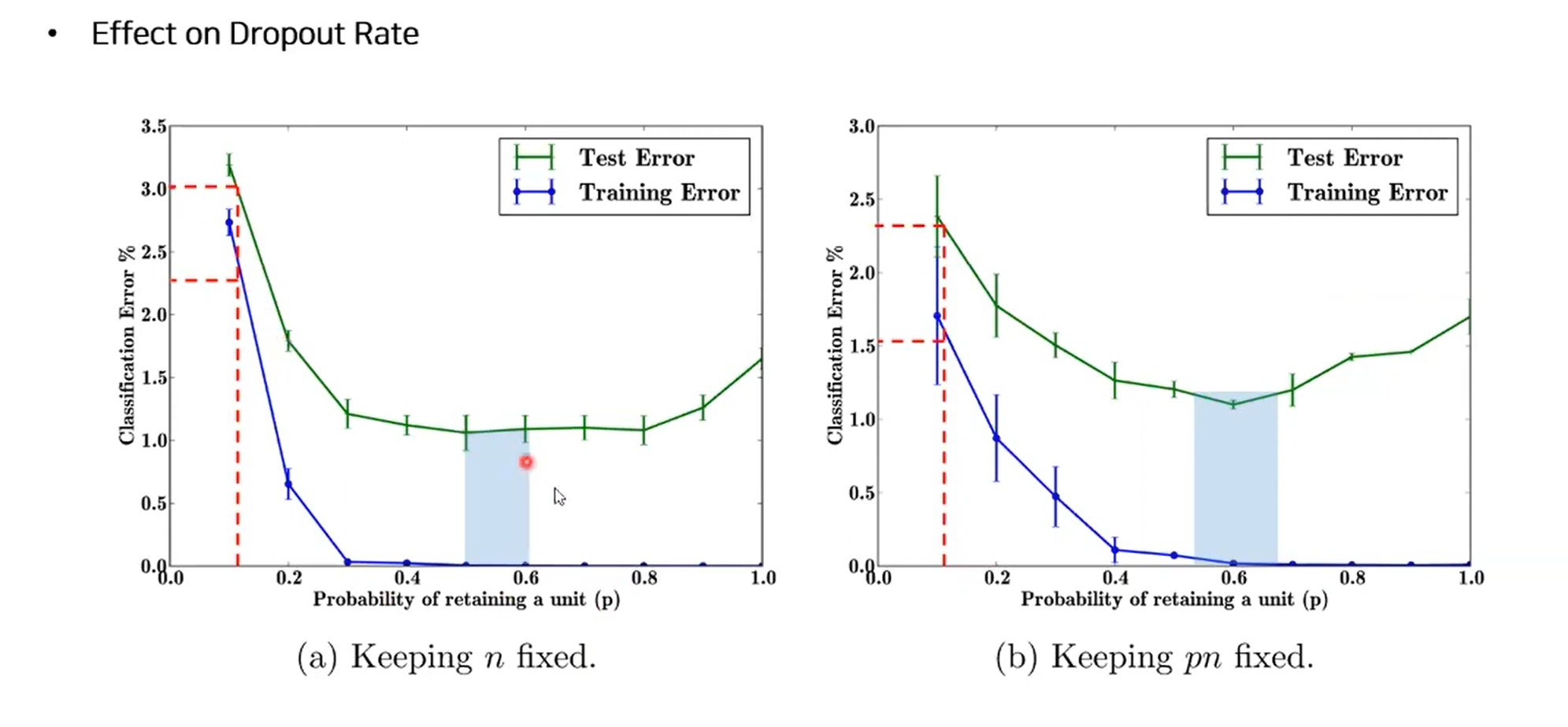
-
p값 따라서 성능 변함
- 0.3 이하에는 underfitting
- 0.8 이상에는 overfitting
-
pn 고정될 때(p, n의 값 곱 고정)
- p 줄면 히든 유닛의 숫자가 커지게 됨
-
결론
- p값이 낮을 때 hidden unit 수를 높여서 에러를 낮출 수 있다.
- p=0.6일 때 최고의 결과
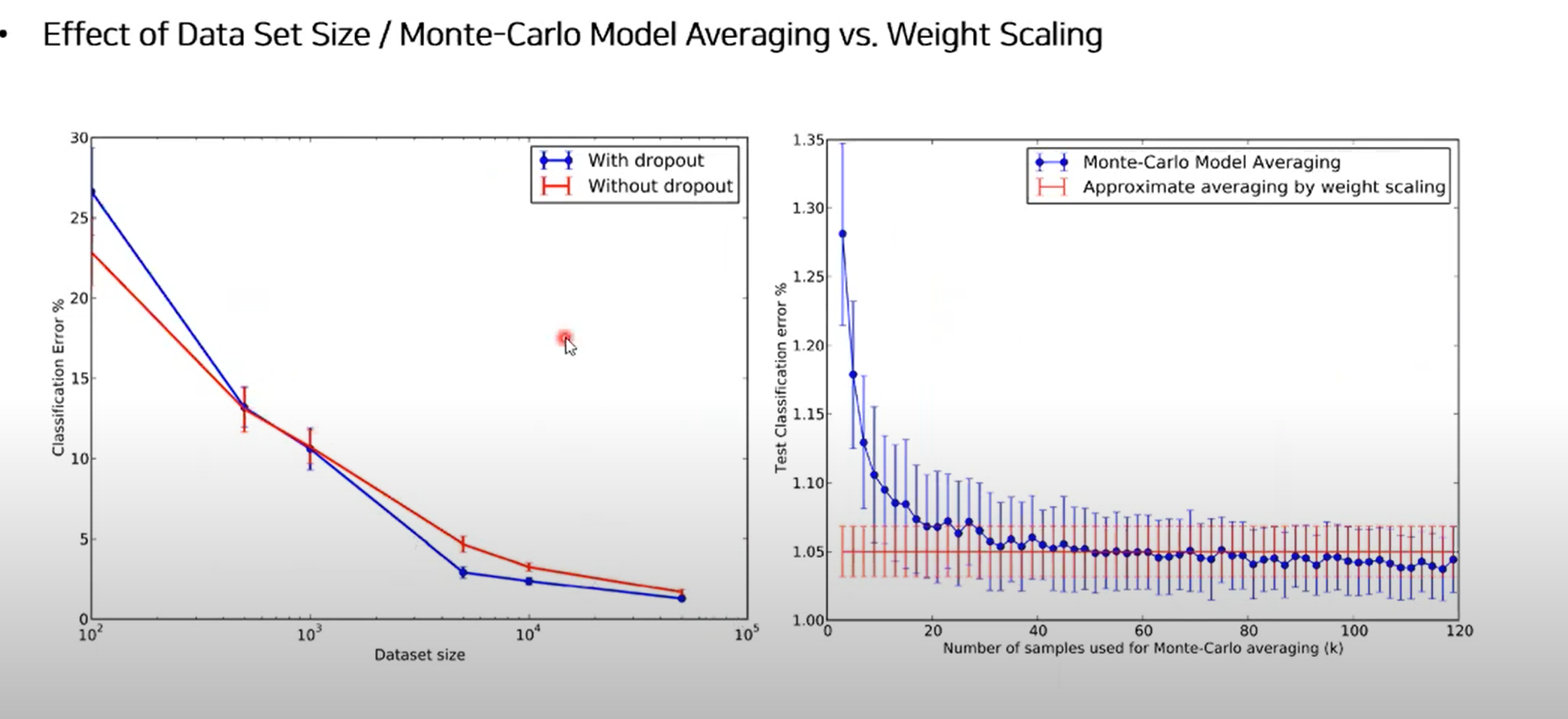
- Dataset size 커질 떄 성능 좋음
- K 값 증가할수록 몬테카를로 average 감소
Restricted Boltzann Machine(RMB)
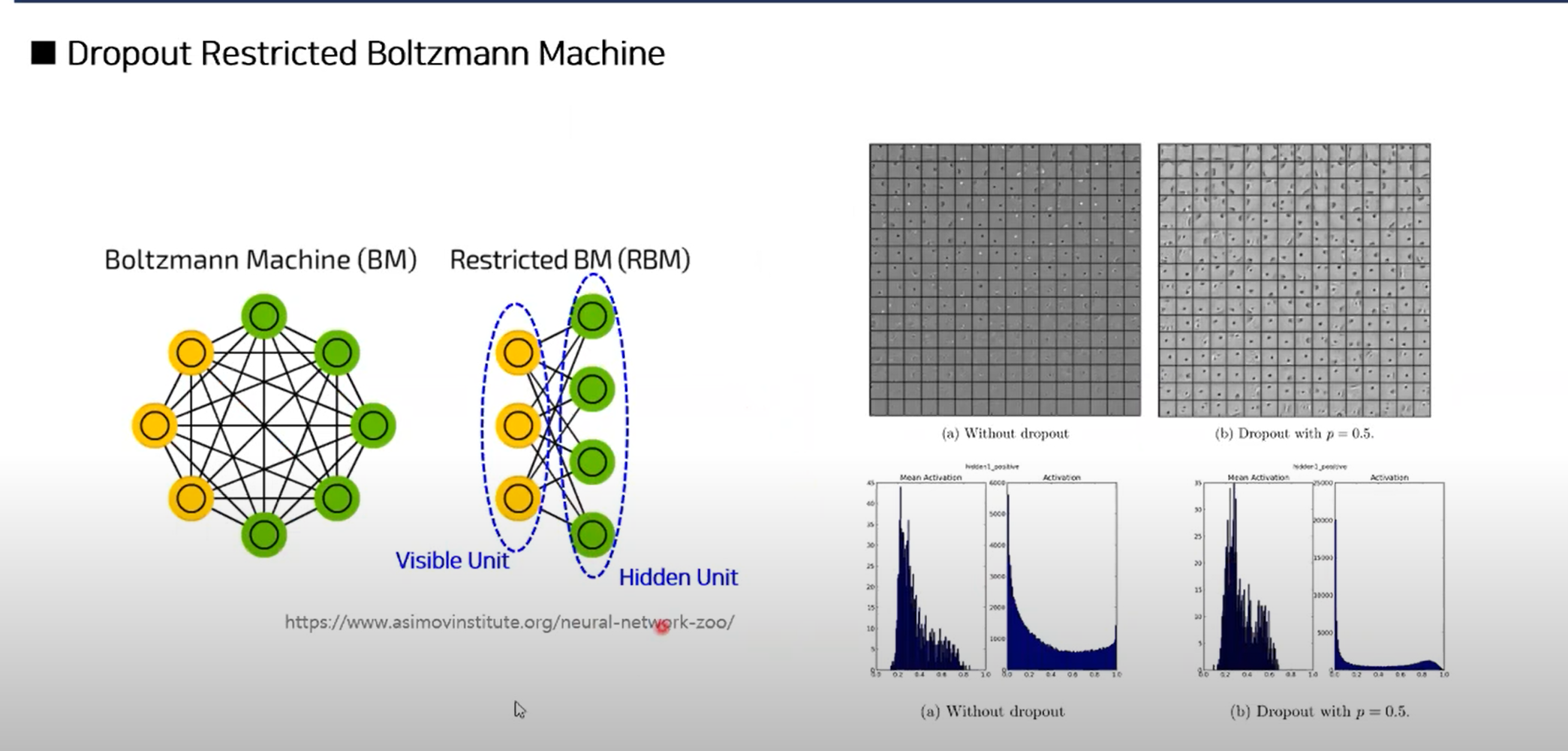
- 입력 히든 유닛간 연결성 없이 고정됨
- FeedFoward network의 한 단일부분로 직관적으로 받아들이면 될듯하다.
- 차이점은: output: NOT determinstic하게 계산하지 않고 probalistic하게 한다.
Conclusion

- 오버피팅을 줄이기 위해 dropout을 사용함
- 여러 도메인에서 적용됨(다양한 데이터셋으로 정리)을 확인
- 다른 graphical model에서도 확장해서 적용 가능
- 단점: training time이 2 ~ 3배 걸림
