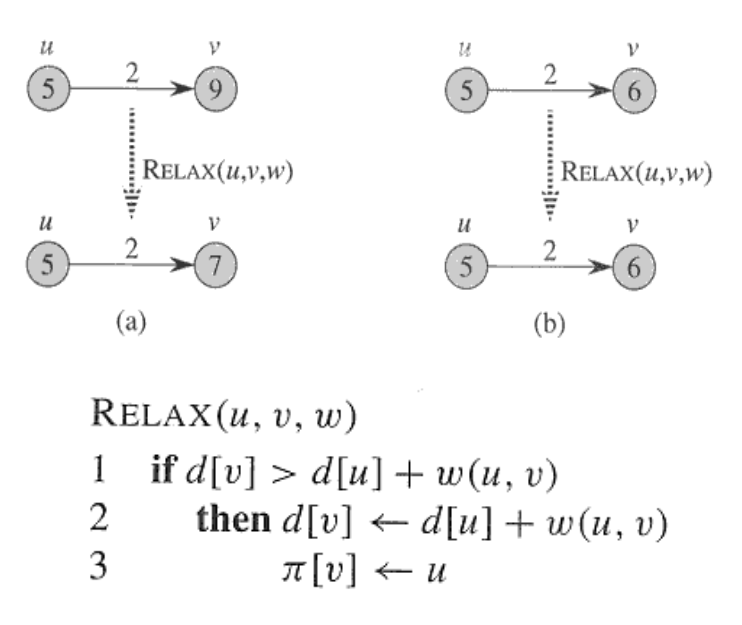
1. Relaxation
최단 거리를 찾는 알고리즘은 Relax를 하는 방식에 따라 나누어진다.
Relax연산은 한 노드 v와 기존의 최단거리 d[v]에 대하여 새로운 Edge를 사용했을 때의 최단거리가 작아지면 d[v]를 업데이트 해준다.
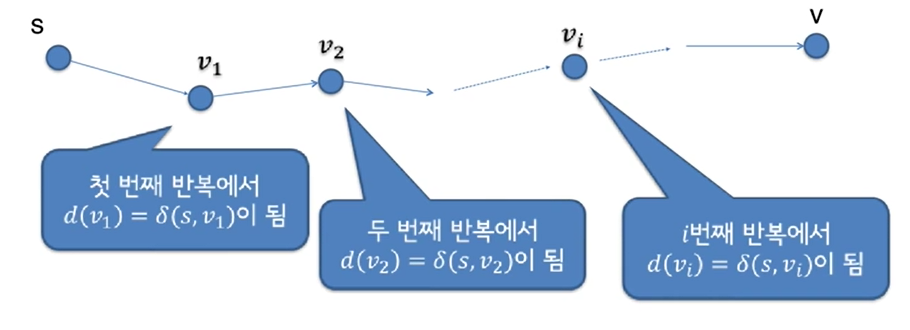
2. Bellman-Ford Algorithm
모든 에지에 대하여 Relax를 1회 실행하면 최단경로의 일부인 δ(s,v1)이 결정된다.
최단 경로는 n-1개의 노드를 포함하므로, Relax 연산을 n-1회 실행하면 된다.

최단 경로를 찾고 난 후에 Relax로 업데이트되는 Edge가 존재한다면, 음수 사이클이 존재한다.
모든 에지에 대해 O(m) Relax 연산을 O(1) n - 1 회 반복 -> O(nm)
하지만 다음과 Worst Case가 발생할 수 있다.
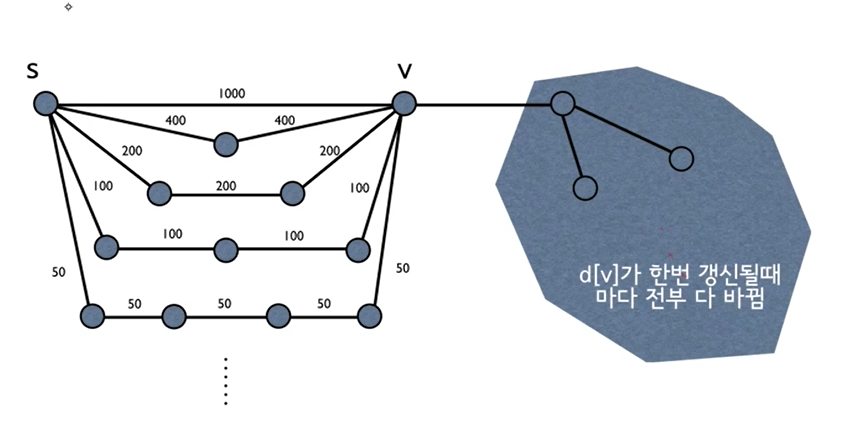
최초 모든 에지에 대해, S와 인접하지 않은 노드부터 Realx가 수행된다면 V는 1000으로 Relax될 수 있다.
다음의 모든 에지에 대해 같은 원리로 V는 800으로 Relax될 수 있는데, 이 경우에 V의 오른쪽에 연결된 subgraph에 포함된 모든 노드는 업데이트 되어야 한다.
3. Dijkstra Algorithm
Dijkstra Algorithm을 통해 위의 Worst Case를 해결할수 있다.
현재까지의 가장 작은 d값을 가진 노드와 연결된 Edge부터 Relax한다.
- 음수 가중치가 없어야 한다.
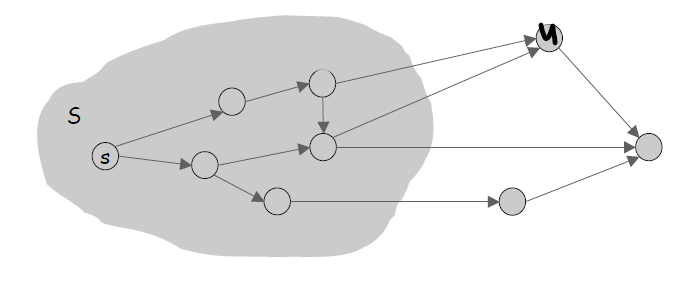
최단경로를 이미 알아낸 노드들의 집합 S에 대하여, S와 연결된 Edge들 중 가장 작은 weight를 가진 Edge를 Relax한다. 이 때 업데이트된 d[u]는 δ(s,u)와 같아지고, u는 S에 포함된다.
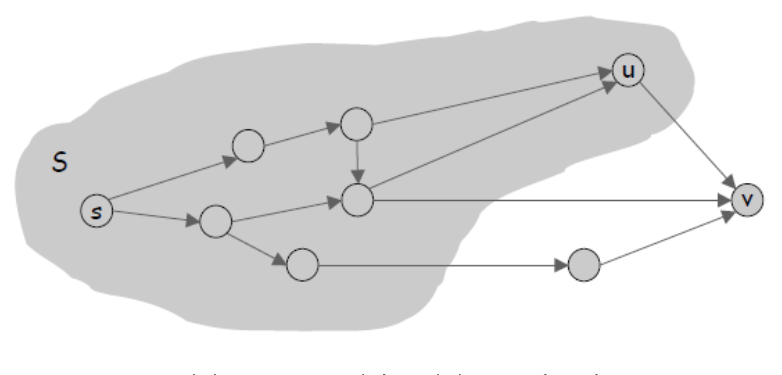

집합 S에 모든 노드들이 포함될 때까지 O(n)
u ∉ S인 d[u] 중 최솟값을 찾은 후 O(n) Relax 실행 O(1)
-> O(n^2)
4. Floyd-Warshall Algorithm
Dynamic Programming을 이용하여 모든 노드 쌍 i, j에 대한 최단경로를 구하는 All-pairs 알고리즘이다.
d^k[i,j]란 노드 i부터 노드 j까지 {1, 2, ... , k}의 노드를지나서 갈 수 있는 최단경로이다.
밑의 그래프와 인정행렬 그래프 d가 있다.
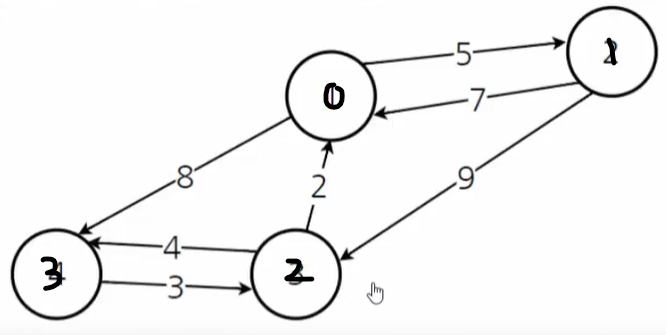
-
d^0[1,3]은 노드 0을 거쳐 1에서 3으로 이동하는 거리로 15 (d[1,0] + d[0,3])의 값을 가진다. 이것은 원래 값 ∞ (d[1,3])보다 작으므로 d에 덮어 씌워진다.
이 때 중간 경로를 나타내는 배열 pi[1,3]의 값은 0이된다. -
d^1[1,3]의 값은 d^0[1,3]: 15 <= d^0[1,1]: 0 + d^0[1,3]: 15 = 15이므로, 이전의 값과 동일하다.
-
d^2[1,3]의 값은 d^1[1,3]: 15 > d^1[1,2]: 9 + d^1[2,3]: 4 = 13이므로, d가 업데이트되고 pi[1,3]의 값은 2가된다.
-
d^3[1,3]의 값은 d^2[1,3]: 13 <= d^2[1,3]: 13 + d^2[3,3]: 0 = 13이므로, 이전의 값과 동일하다.
따라서 k가 0부터 n까지 모든 i,j에 대하여 차례대로 최단 경로가 계산되므로 다음과 같은 점화식을 만들 수 있다.

k를 나타내기위해 3차원 배열을 사용할 필요 없이 d^k-1[i,j]는 dk-1[i,j]를 계산할 때만 필요하므로 i와 j를 나타내기 위한 2차원 배열을 사용하면 된다.
2차원 배열에서 차례로 업데이트를 진행하다 보면 d^k[i,j] = d^k[i,k] + d^k[k,j]와 같이 이미 덮어 씌워진 값으로 d^k가 계산되는 경우가 있다.
d^k[i,k]의 의미를 생각해 보면, i부터 k까지 {1, 2, ..., k}의 노드들을 지나는 최단경로이므로 이는 d^k-1[i,k]와 같다.


시간복잡도는 O(n^3)이다.