1. MST
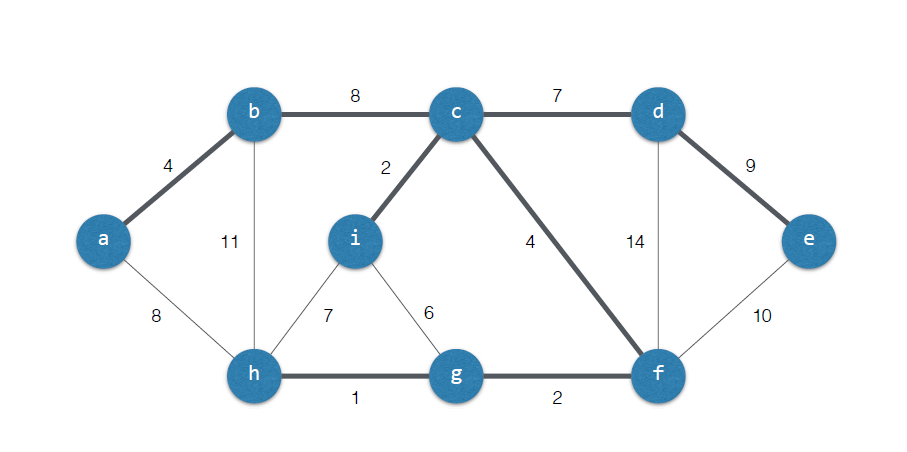
모든 Vertex들을 연결하는 트리.
트리: Cycle이 없는 연결된 무방향 그래프
따라서 MST의 edge의 개수는 Vertex의 개수 - 1이 된다.
2. Kruskal's Algorithm
알고리즘

- 모든 에지들을 가중치의 오름차순으로 정렬한다.
- 가중치가 작은 순서로 에지를 선택해가며 Cycle이 만들어지지 않는다면 MST에 포함한다.
- n - 1개의 에지가 선택되면 종료한다.
MAKE-SET: O(n)
FIND-SET:O(n)을 모든 Edge에 대해서 반복: O(mn)
Weighted Union & Path Compressison (WUPC)으로 상향 Tree의 높이를 줄일 경우, Find와 Union 연산을 O(M)으로 줄일 수 있다.
따라서 시간복잡도는 모든 에지를 정렬하는 O(mlogm) = O(mlogn)이 된다.
Cycle 검사
모든 Vertex를 각각 집합으로 나누어 두 Vertex가 연결되는 경우 두 집합을 합집합한다.
두 Vertex를 연결했는데 같은 집합안에 있는 경우 Cycle을 형성한다.
구현
- 집합
: 상향식 트리 자료구조를 이용한다.
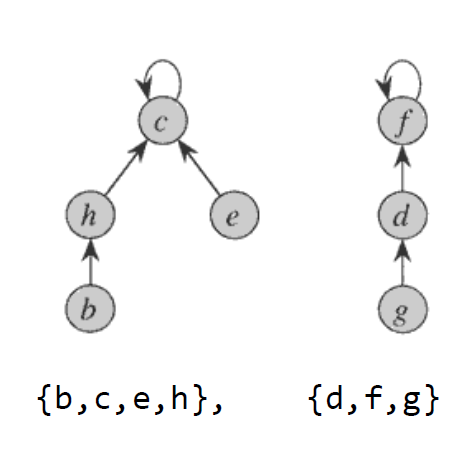
-
Cycle 확인: 두 veretx의 부모 노드가 같다면 같은 집합 내에 있다.
-
합집합: 한 vertex의 부모를 다른 vertex로 설정한다.
코드
/*
* Kruskal's Algorithm
*/
/*
* Sorting edge array
*/
typedef struct Edge {
int s;
int d;
int w;
}Edge;
void swap(Edge* a, Edge* b) {
Edge temp;
temp = *a;
*a = *b;
*b = temp;
}
void SortEdges(Graph* g, int m, Edge* edges) {
for (int i = m - 1; i >= 0; i--) {
for (int j = 0; j < i; j++) {
if (edges[j].w > edges[j + 1].w) {
swap(&edges[j], &edges[j + 1]);
}
}
}
};
int count_edges(Graph* g, int V) {
int m = 0;
AdjNode* c;
for (int i = 0; i < V; i++) {
c = g->array[i].head;
while (c != NULL) {
m++;
c = c->next;
}
}
return m;
}
/*
* Finding cycle
*/
typedef struct TreeNode {
int v;
struct TreeNode* p;
}TreeNode;
typedef struct Tree {
TreeNode* root;
}Tree;
TreeNode* find_root(TreeNode* x) {
if (x != x->p)
x->p = find_root(x->p);
return x->p;
}
void union_tree(TreeNode* u, TreeNode* v) {
TreeNode* x = find_root(u);
TreeNode* y = find_root(v);
x->p = y;
}
void Kruscal(Graph* mst, Graph* g, int V) {
// save and sort edges
int m = count_edges(g, V);
Edge* edges = (Edge*)malloc(sizeof(Edge) * m);
AdjNode* c;
int j = 0;
for (int i = 0; i < V; i++) {
c = g->array[i].head;
while (c != NULL && j < m) {
edges[j].s = i;
edges[j].d = c->dest;
edges[j].w = c->weight;
c = c->next;
j++;
}
}
SortEdges(g, m, edges);
// make set
Tree* tree = (Tree*)malloc(sizeof(Tree) * V);
TreeNode* treeNode = (TreeNode*)malloc(sizeof(Tree) * V);
for (int i = 0; i < V; i++) {
treeNode[i].v = i;
treeNode[i].p = &treeNode[i];
tree[i].root = &treeNode[i];
}
// make mst
int k = 0;
int n = 0;
while (k < m && n < V-1){
// if the edge doesn't make cycle
if (find_root(&treeNode[edges[k].s]) != find_root(&treeNode[edges[k].d])) {
add_edge(mst, edges[k].s, edges[k].d, edges[k].w);
union_tree(&treeNode[edges[k].s], &treeNode[edges[k].d]);
n++;
}
k++;
}
}3. Prim's Algorithm
알고리즘
-
MST의 부분집합 V가 있다.
-
key[i]는 V로부터의 최단거리를, pi[i]는 최단거리를 갖는 vertex를 의미한다.
-
시작점 부터 시작해 가장 작은 key값을 가지는 veretx를 V에 포함시킨다.
-
V에 포함된 vertex와 연결되어 있는 vertex들의 key와 pi를 업데이트한다.
수도코드

시간복잡도
-
최소의 key값을 가진 vertex를 찾는데 O(n)
-
그 vertex와 연결된 vertex들의 key와 pi를 업데이트 하는데 O(n)
-
총 n-1번 실행하므로 시간복잡도는 O(n^2)이다.
최소의 key값을 가진 vertex를 찾는데 최소 우선순위 큐를이용할 수 있다.

- Vertex의 정보를 최소 우선순위 큐에 삽입한다. O(logn)
- 최소의 key값을 가진 vertex를 찾는다. O(logn)
- 그 vertex에 연결된 vertex들의 정보를 업데이트한다.
(vertex의 key값이 원래의 값보다 작아지게 되면 heapify가 필요하다.)
모든 노드의 연결된 vertex에 대하여 실행하므로 O(m*logn)
코드
/*
* Prim's Algorithm
*/
int* Prim(Graph* g, int V, int r) {
int* key = (int*)malloc(sizeof(int) * V);
int* pi = (int*)malloc(sizeof(int) * V);
bool* visited = (bool*)malloc(sizeof(bool) * V);
for (int i = 0; i < V; i++) {
key[i] = INT_MAX;
pi[i] = NULL;
visited[i] = false;
}
AdjNode* c;
int min = INT_MAX;
int min_idx = r;
visited[r] = true;
for (int i = 0; i < V - 1; i++) {
c = g->array[min_idx].head;
while (c != NULL) {
if (visited[c->dest] == false && key[c->dest] > c->weight) {
key[c->dest] = c->weight;
pi[c->dest] = min_idx;
}
c = c->next;
}
min = INT_MAX;
//find min idx
for (int i = 0; i < V; i++) {
if (key[i] < min && visited[i] == false) {
min = key[i];
min_idx = i;
}
}
visited[min_idx] = true;
}
return pi;
}
