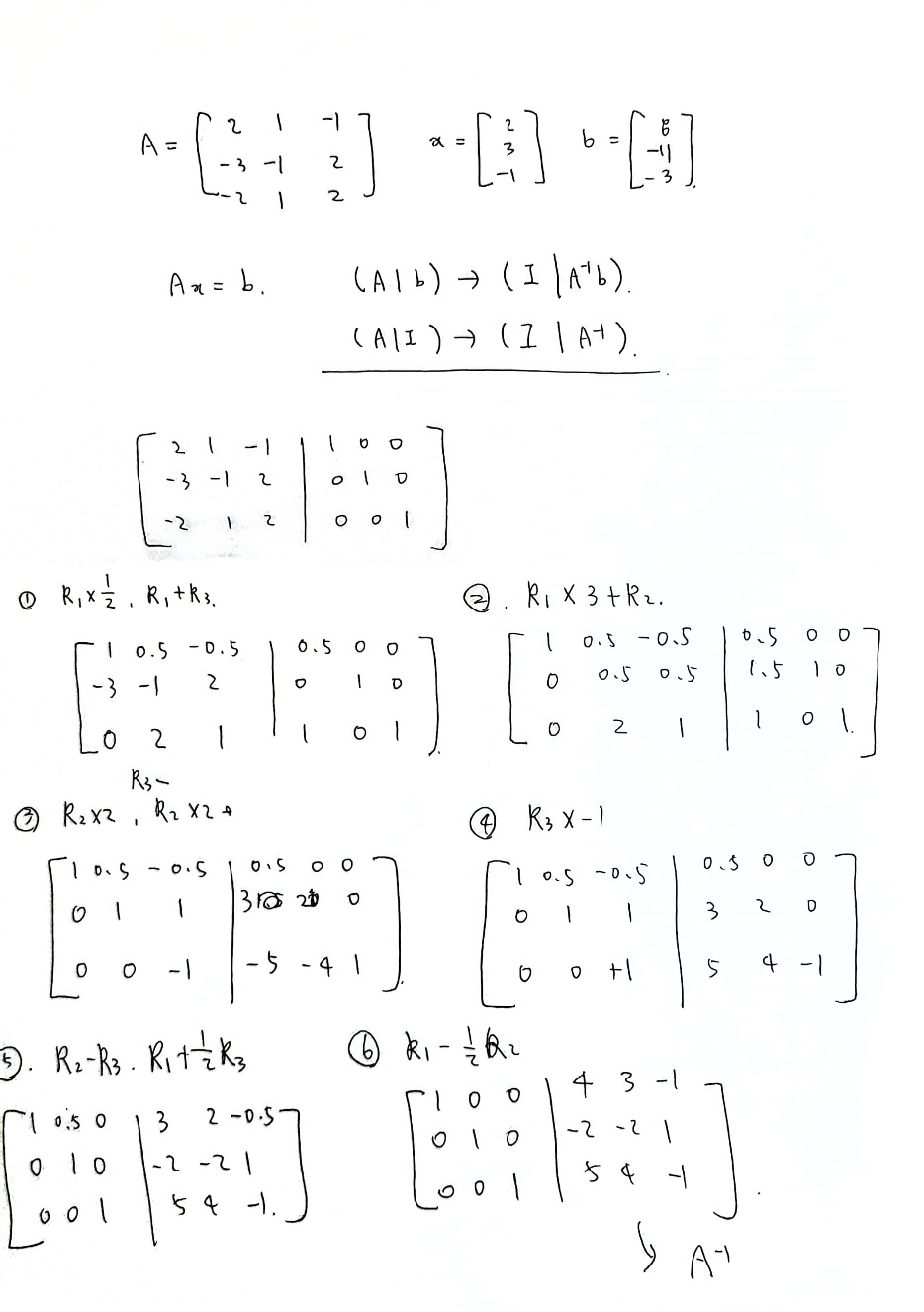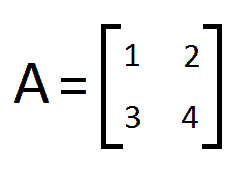응용수학 복습 4

Ax = b 형태의 비동차 선형 연립 방정식에서 x를 구하는 방법

• A가 정방행렬이고 행렬식이 0이 아니다.

  • 역행렬을 구해 x = A^(-1)b에 대입한다.
    • 여인수 전개

• A가 m x n의 직사각행렬이다.

  • 의사 역행렬을 구해 A^(-1) 대신 대입한다.
  • m보다 n이 크다. (방정식의 개수보다 미지수의 개수가 많다.)
    • 우 의사 역행렬 A^(T)(AA^(T))^(-1)
  • m이 n보다 크다. (방정식의 개수가 미지수의 개수보다 많다.)
    • 좌 의사 역행렬 ((A^(T)A))^(-1)A^(T)

• x를 구하는 알고리즘

  • 크래머 공식
  • 가우스 소거법
  • 가우스-조던 소거법

• 고유값, 고유벡터

• 특이값, 고유벡터

1. 크래머 공식

: Ax = b에서 A의 i번째 열을 b로 치환한 A_i(b) 행렬을 이용하여 x를 구하는 공식

1) 공식

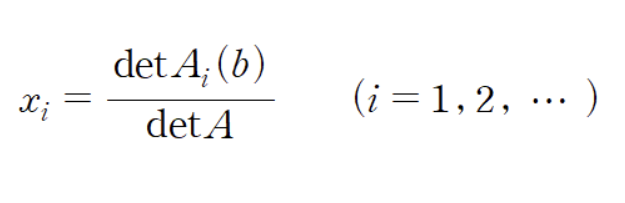
2) 예제

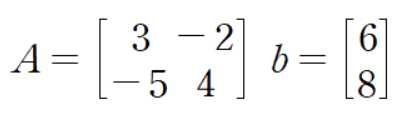
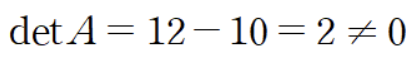
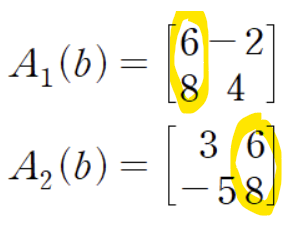
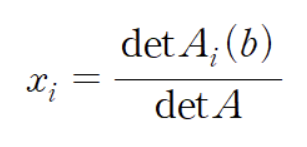
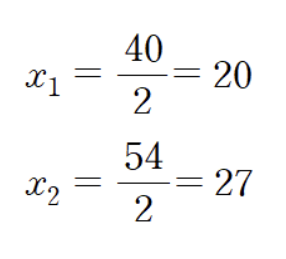
2. 가우스 소거법

: 행렬 A와 b로 이루어진 첨가 행렬 [A|b] (Augmented Matrix)를 가우스 소거법 (기본 행 연산)을 이용해 행사다리꼴 행렬로 만든다.

: 밑의 행으로 갈수록 미지수의 개수가 작아지므로 선형 방정식의 해를 쉽게 구할 수 있다.

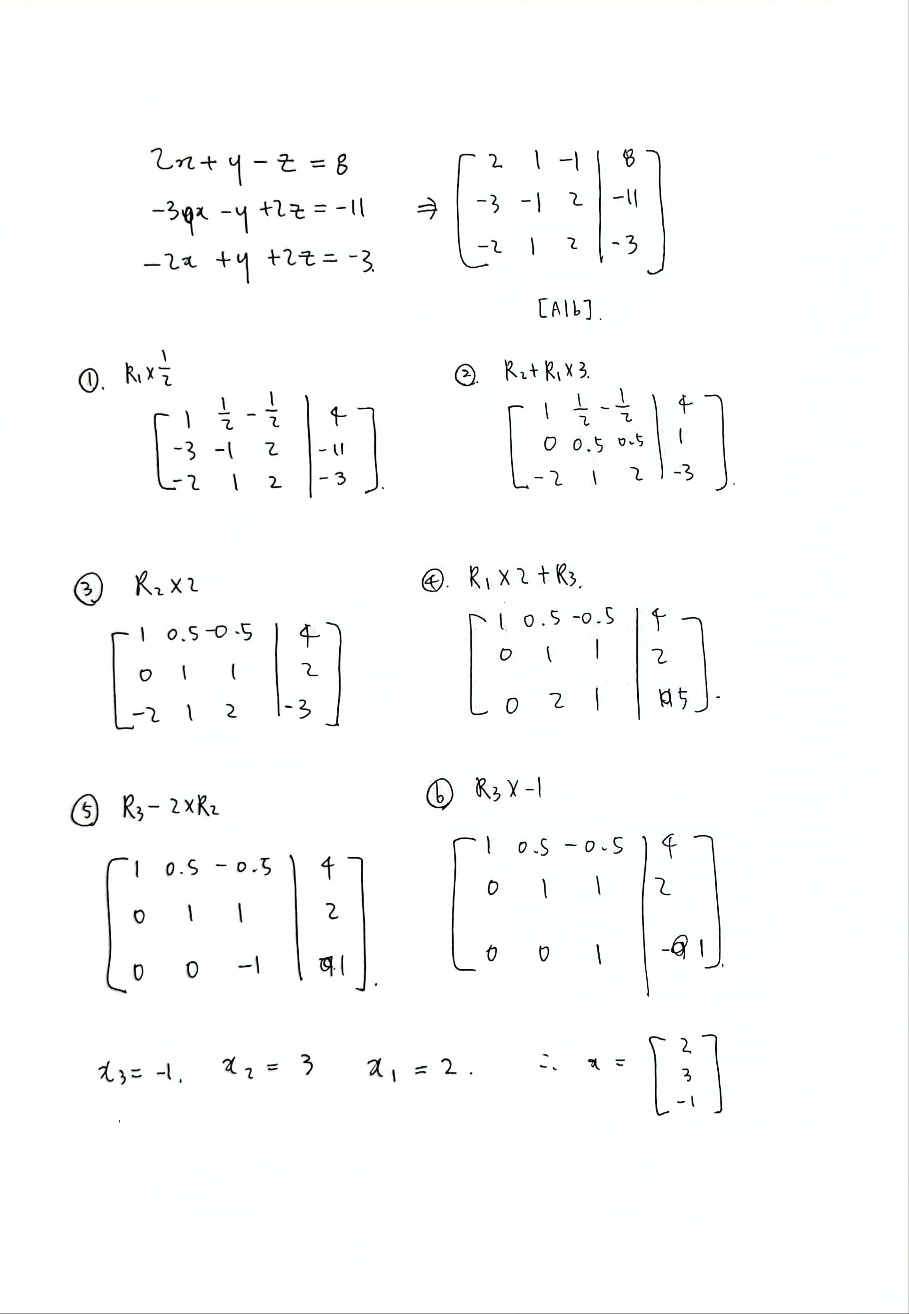
3. 가우스-조던 소거법

: 첨가 행렬을 기약 행 사다리꼴로 만든다.

: 선형 방정식의 해 벡터를 바로 구할 수 있다.

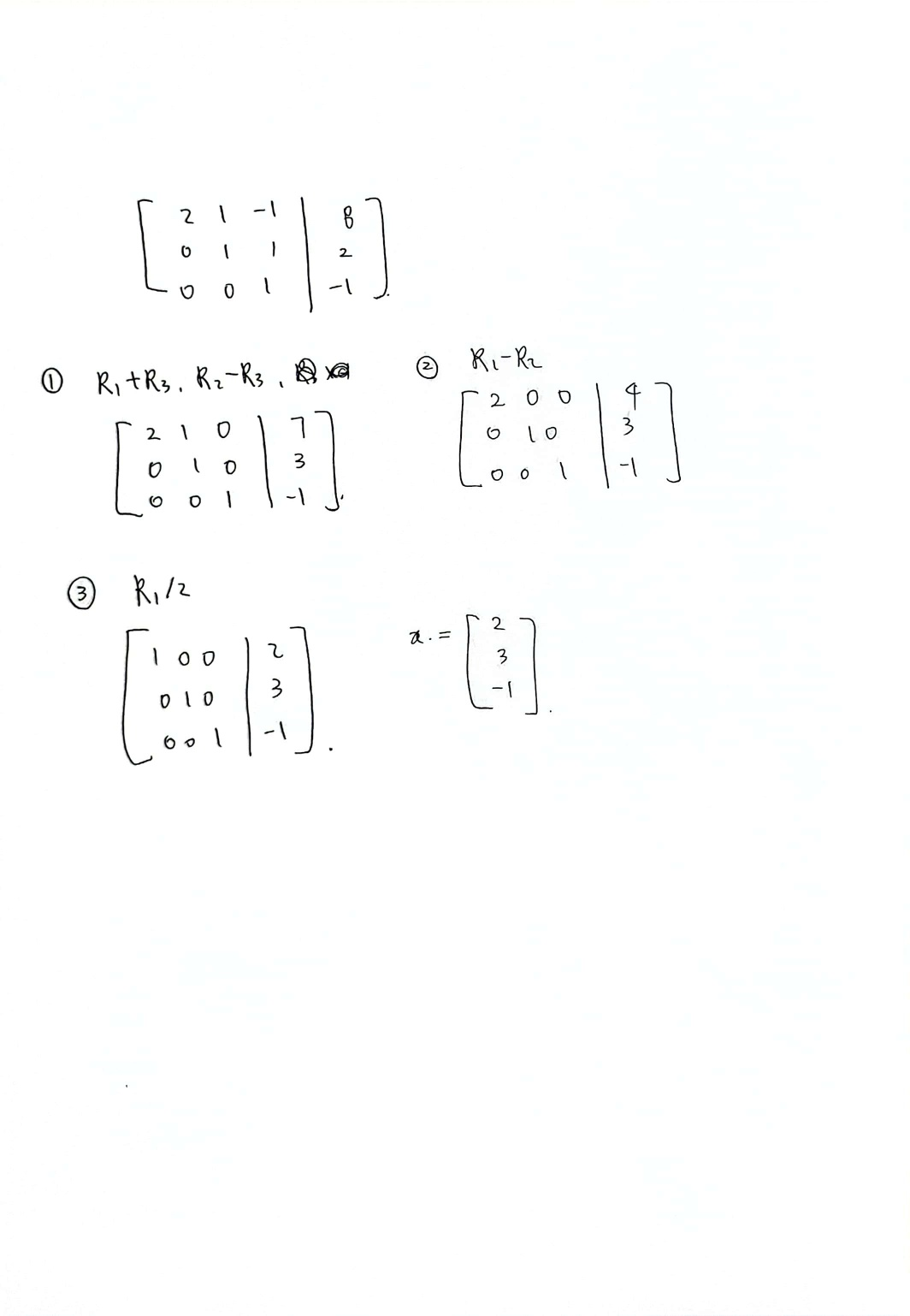
: 행렬에 b 대신 I를 첨가하면 역행렬을 구할 수 있다.