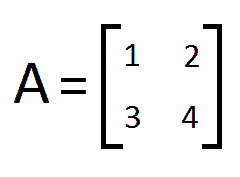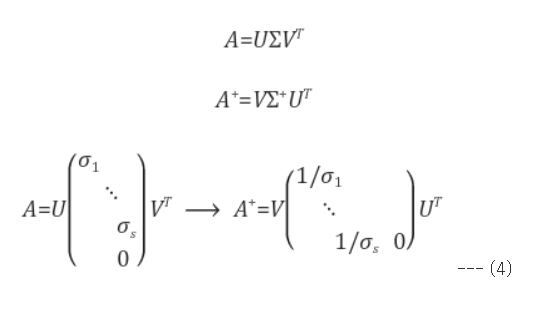Ax = b의 비동차 선형 연립 방정식에 대하여
-
A가 정방행렬이다.
- det(A)가 0이 아니다. (선형 독립이다.)
- 역행렬을 구해 b에 곱해준다.
- 여인수 전개
- A를 고유값 분해한 후 역행렬을 구한다.
- 역행렬을 구해 b에 곱해준다.
- det(A)가 0이 아니다. (선형 독립이다.)
-
A가 정방행렬이 아니다. (m x n 차원이다.)
- 의사역행렬을 구해 b에 곱해준다.
- m < n이다. (방정식 보다 미지수의 개수가 많다.)
: 우 의사 역행렬 A'(AA')^(-1) - m > n이다. (방정식이 미지수의 개수보다 많다.)
: 좌 의사 역행렬 (A'A)^(-1)A'
- m < n이다. (방정식 보다 미지수의 개수가 많다.)
- 의사역행렬을 구해 b에 곱해준다.
- A가 det(A) = 0 (선형 종속)이거나 정방행렬이 아니다.
- A를 특이값 분해한 후 역행렬을 구한다.
- 비동차 선형 연립 방정식의 해를 구하는 알고리즘
- 크래머 공식
- 가우스 소거법
- 가우스-조던 소거법
- (A|I) 첨가행렬로 역행렬도 구할 수 있다.
1. 고유값 분해
1) 정의
m x m 행렬 A에 대해 고유값 (eigen value) λ와 고유벡터 (eigen vector) v는 다음 식을 만족한다.

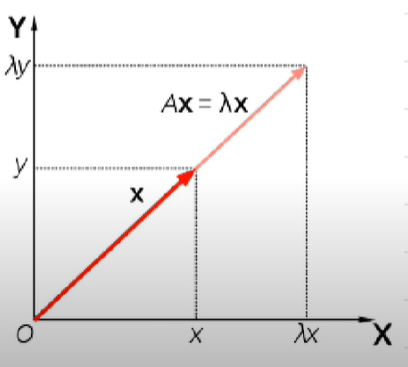
2) 기하학적 의미
고유벡터 x에 선형변환 (A) 했을 때 크기만 변하고 (λ 스칼라 배) 방향은 변하지 않는다.
3) 예제

선형변환 A가 주어졌을 때 고유벡터1 (v1, v2)는 A에 의해 1배 (λ1) 되고, 고유벡터 2 (w1, w2)는 A에 의해 3배 (λ2) 된다.
선형변환 전
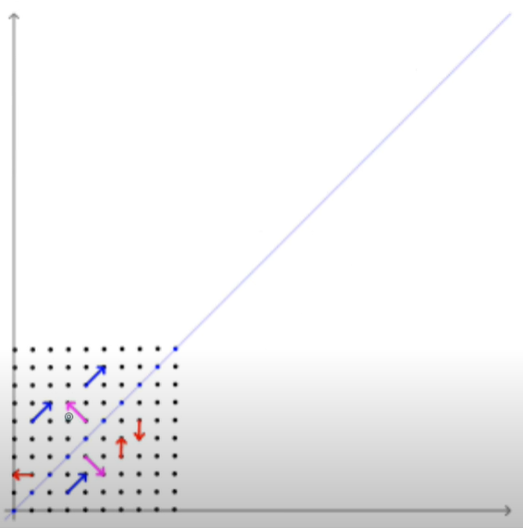
선형변환 후
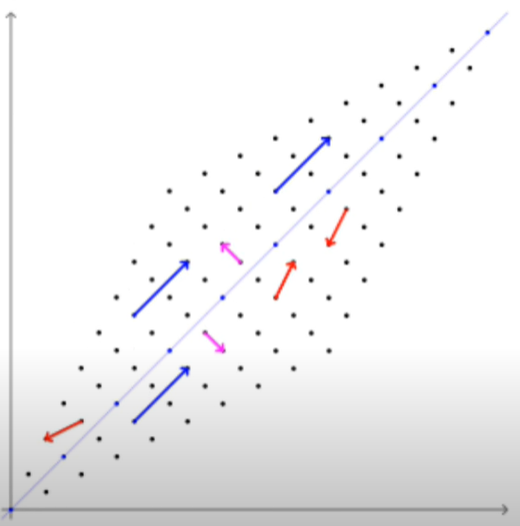
선형변환 후에도 방향이 같은 벡터는 파란색과 빨간색이 있고, 각각 크기만 3배, 1배 되었음을 확인할 수 있다.
4) 고유값 분해
행렬 A와 고유벡터와 고유값의 관계는 다음과 같다.
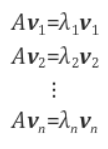
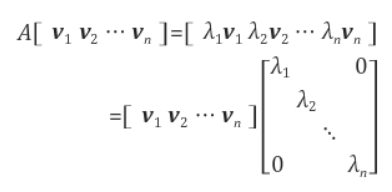
고유벡터를 열벡터로 하는 행렬을 P, 고유값들로 이루어진 대각행렬을 Λ라 하면 다음 식이 성립한다.
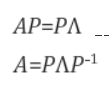
5) 예제

6) 결과
행렬을 고유값 분해하면 행렬식과 역행렬을 쉽게 구할 수 있다.
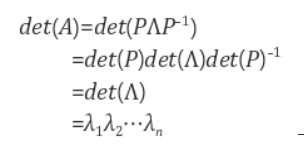
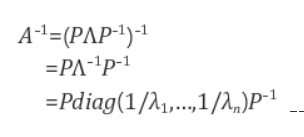
2. 특이값 분해
1) 직교행렬
행렬 A와 전치행렬 A'의 내적이 I가 될 때 A를 직교행렬이라고 한다.

A가 직교행렬일 때 AAT = ATA = E, A-1 = AT를 만족한다.
1) 정의
특이값 분해는 ATA와 AAT는 정방행렬이 됨을 이용한다. 따라서 모든 m x n 행렬에 대해 적용 가능하다.

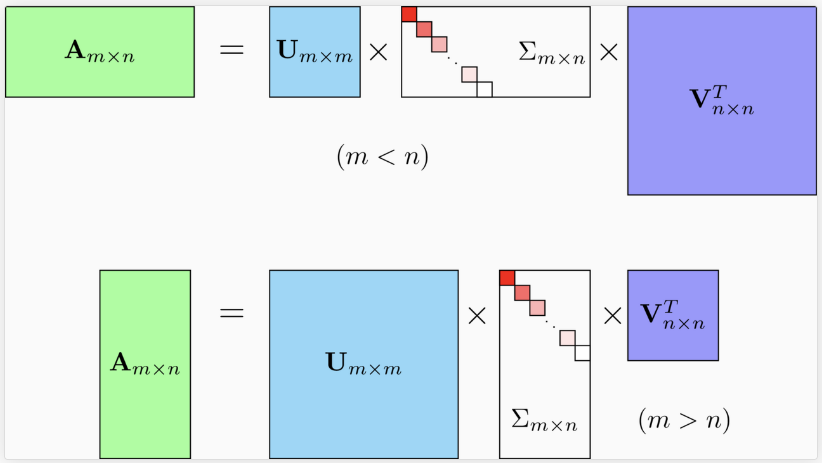
좌 특이벡터 U의 열벡터(ui): AAT (m x m)의 eigenvector
우 특이벡터 V의 열벡터(vi): A'A (n x n)의 eigenvector
특이값 Σ의 대각원소(σi): A'A, AA'의 eigenvalue들의 square root
(대각 원소를 제외한 원소는 0으로 채운다.)
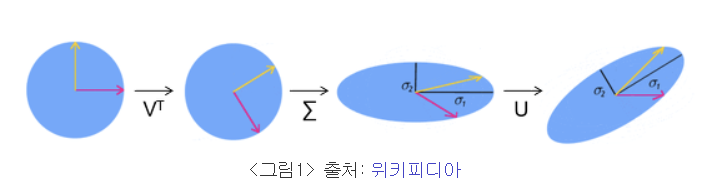
2) 기하학적 의미
AV = UΣ
: 직교행렬 V에 행렬 A를 선형변환 해주면 Σ만큼 크기가 변하지만 여전히 직교하는 행렬 U가 된다.
2) 예제

3) 결과
특이값 분해를 이용해면 의사 역행렬을 다음과 같이 쉽게 구할 수 있다.
A가 직교행렬일 A-1 = AT이므로
U, V의 순서가 바뀌고 Σ도 m x n에서 n x m 행렬로 바뀜에 주의하자.
3. 케일리-헤밀턴 정리
정방행렬A의 특성방정식에서 λ대신 A를 대입해도 식을 만족한다.
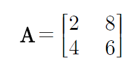
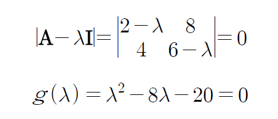
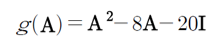
멱승을 구하는데 편리하다.
A^2 = 8A + 20I
역행렬을 구할 수 있다.
A(A - 8I) = 20I
A(1/20(A - 8I)) = I
A^-1 = 1/20(A - 8I)