[자료구조와 알고리즘 with 파이썬] 04 트리

찬은·2025년 3월 29일

자료구조와 알고리즘 with 파이썬

목록 보기

4/10

04-1 트리란?
04-2 이진 트리
04-3 이진 트리의 연산
04-4 모스 코드 결정 트리
04-5 수식 트리

04-1 트리란?

트리

계층적인 관계를 가진 자료의 표현에 유용하게 사용됨

트리의 사용

우선순위 큐를 효율적으로 구현
결정 트리(decision tree): 의사결정 구조 표현

트리 관련 용어

노드(node)

트리에서 각각의 요소들
트리는 하나 이상의 노드들로 이루어짐

간선 or 에지(edge)

노드와 노드의 연결 관계

루트(root)

계층적인 구조에서 가장 높은 곳에 있는 노드

트리의 모든 노드는 자신을 루트로하는 하나의 서브 트리를 대표함

트리의 표현 방법

트리는 중첩된 집합으로 나타낼 수 있음
트리의 루트와 서브 트리를 중첩된 괄호로 묶어 하나의 문자열처럼 표현할 수 있음
들여쓰기로도 나타낼 수 있음

일반 트리의 표현

N-링크 표현

차수가 N인 노드와 N개의 링크를 갖도록 허용
노드마다 링크의 개수가 다름

왼쪽 자식-오른쪽 형제 표현

하나의 링크는 왼쪽 자식을 가리키고, 다른 하나는 오른쪽 형제를 가리키기 위해 사용
형제 노드 사이에 순서가 있음
목표 노드까지 찾아가는 과정에서 많은 노드를 거쳐야 함

Quiz

(a) A
(b) D
(c) H, I
(d) 3
(e) 4
(f) 3

(a)
(b) (A (B (E)(F)) (C (G)(H)(I)) (D (J (K)(L)))

04-2 이진 트리

이진 트리(binary tree)

모든 노드가 최대 2개의 자식만을 가질 수 있는 트리
왼쪽 자식과 오른쪽 자식은 반드시 구별되어야 함

이진 트리의 사용

이진 탐색 트리(binary search tree)
힙 트리(heap tree)
수식 트리(expression tree)

이진 트리의 종류

포화 이진 트리

트리의 각 레벨에 노드가 꽉 차있는 이진 트리
트리의 높이를 알면 전체 노드의 수를 알 수 있음
각 노드에 순서대로 번호를 붙일 수 있음

완전 이진 트리

높이가 k인 트리에서 레벨 1부터 k-1까지는 노드가 모두 채워져 있고, 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진 트리
마지막 레벨에서는 노드가 꽉 차 있지 않아도 되지만, 빈 곳이 있으면 안 됨

균형 이진 트리

모든 노드에사 좌우 서브 트리의 높이 차이가 1 이하인 트리

경사 이진 트리

좌우 서브 트리의 높이 차이가 2인 트리

이진 트리의 표현 방법

배열 구조 표현

(1) 트리의 높이를 구해 배열(또는 파이썬의 리스트)을 할당함

높이가 $k$ 이면 길이가 $2^k - 1$ 인 배열이 필요함
(2) 포화 이진 트리의 번호를 인덱스로 사용해 배열에 노드들을 저장함

노드 i의 부모 노드 인덱스 = i/2

노드 i의 왼쪽 자식 노드 인덱스 = 2i

노드 i의 오른쪽 자식 노드 인덱스 = 2i + 1

연결된 구조 표현: 링크 표현법

class BTNode:
   def __init__(self, elem, left=None, right=None):
     self.data = elem
     self.left = left
     self.right = right

Quiz

9

31

16, 31

6

04-3 이진 트리의 연산

이진 트리의 표준순회

순회

모든 노드를 한 번씩 방문하는 것

전위 순회

def preorder(n):
  if n is not None:
    print(n.data, end=' ')
    preorder(n.left)
    preorder(n.right)

중위 순회

def inorder(n):
  if n is not None:
    inorder(n.left)
    print(n.data, end=' ')
    inorder(n.right)

후위 순회

def postorder(n):
  if n is not None:
    postorder(n.left)
    postorder(n.right)
    print(n.data, end=' ')

순회 방법의 선택

어떤 폴더의 용량은 하위 폴더들의 용량을 알아야만 계산할 수 있음 -> 후위순회 사용
부모의 레벨이 결정되어야 자식의 레벨을 결정할 수 있음 -> 전위순회 사용

레벨 순회

레벨 순으로 노드 방문
큐를 이용해 구현

def levelorder(root):
  queue = ArrayQueue()
  queue.enqueue(root)
  while not queue.isEmpty():
    n = queue.dequeue()
    if n is not None:
      print(n.data, end=' ')
      queue.enqueue(n.left)
      queue.enqueue(n.right)

이진 트리의 연산들

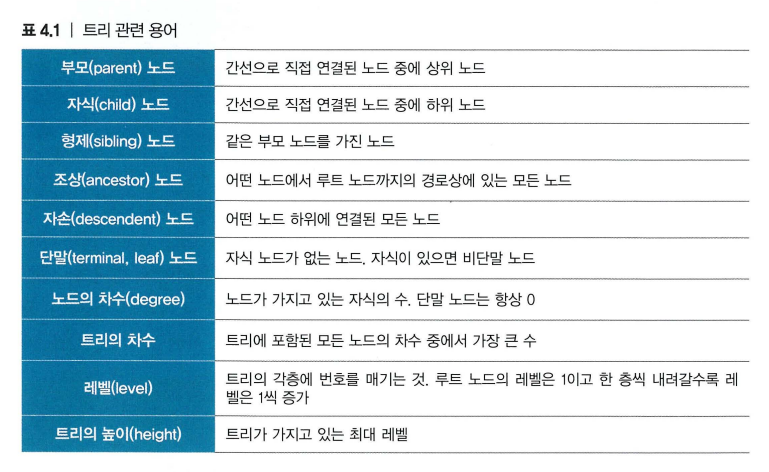
전체 노드의 수 구하기

def count_node(n):
  if n is None:
    return 0
  else:
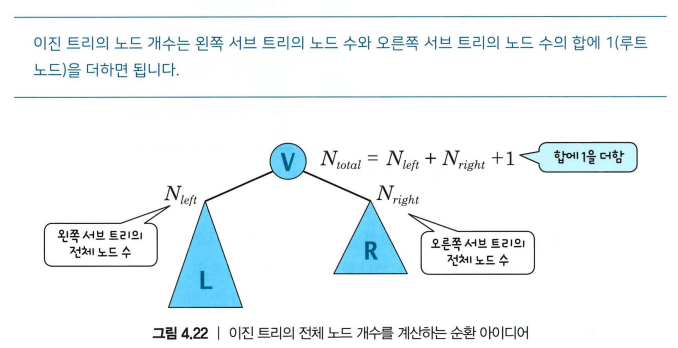
    return count_node(n.left) + count_node(n.right) + 1

트리의 높이 구하기

def clac_height(n):
  if n is None:
    return 0
  hLeft = clac_height(n.left)
  hRight = clac_height(n.right)
  if (hLeft > hRight):
    return hLeft + 1
  else: return hRight + 1

테스트 프로그램

코드

d = BTNode('D', None, None)
e = BTNode('E', None, None)
b = BTNode('B', d, e) 
f = BTNode('F', None, None)
c = BTNode('C', f, None)
root = BTNode('A', b, c)

print('\n In-Order : ', end=' '); inorder(root)
print('\n Pre-Order : ', end=' '); preorder(root)
print('\n Post-Order : ', end=' '); postorder(root)
print('\n Level-0rder : ', end=' '); levelorder(root)
print()

print(" 노드의 개수 = %d 개" % count_node(root))
print(" 트리의 높이 = %d" % calc_height(root))

실행 결과

In-Order : D B E A F C
Pre-Order : ( A ( B (D) (E) ) ( C (F) ) )
Post-Order : D E B F C A 
Level-0rder : A B C D E F
노드의 개수 = 6개
트리의 높이 = 3

Quiz

(전위) 24 19 15 11 17 23 20 42 41 28 55
(중위) 11 15 17 19 20 23 24 28 41 42 55
(하위) 11 17 15 20 23 19 28 41 55 42 24
def preorder(n):
  if n is not None:
    print("(", end='')
    print(n.data, end=' ')
    print(")", end='')
    preorder(n.left)
    preorder(n.right)

04-4 모스 코드 결정 트리

모스 코드(Morse Code)

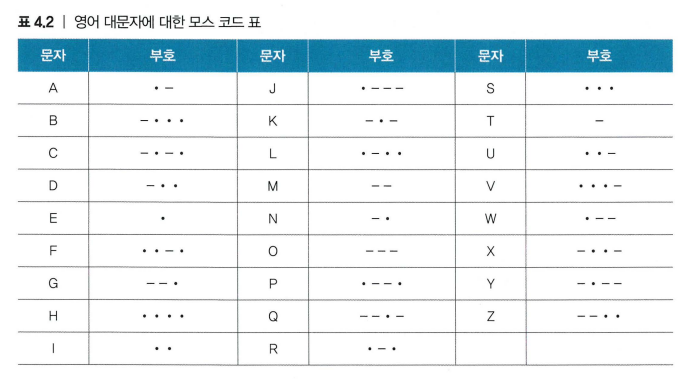
문자를 모스 코드로 변환하는 과정: 인코딩

부호화 or 인코딩(encoding)

문자열을 모스 코드로 바꾸는 것

def encode(ch):
  idx = ord(ch)-ord('A')
  return table[idx][1]

모스 코드를 문자로 변환하는 과정: 디코딩(decoding)

복호화 or 디코딩(decoding)

모스 코드가 주어졌을 때 해당하는 알파벳을 추출하는 것

def decode_simple(morse):
  for tp in table:
    if morse == tp[1]:
      return tp[0]

표의 크기가 n개라면 n번 비교해야함 -> 비효율적

결정 트리를 이용한 모스 코드의 디코딩

결정 트리

여러 단계의 복잡한 조건을 갖는 문제에 대해 조건과 그에 따른 해결 방법을 트리 형태로 나타낸 것

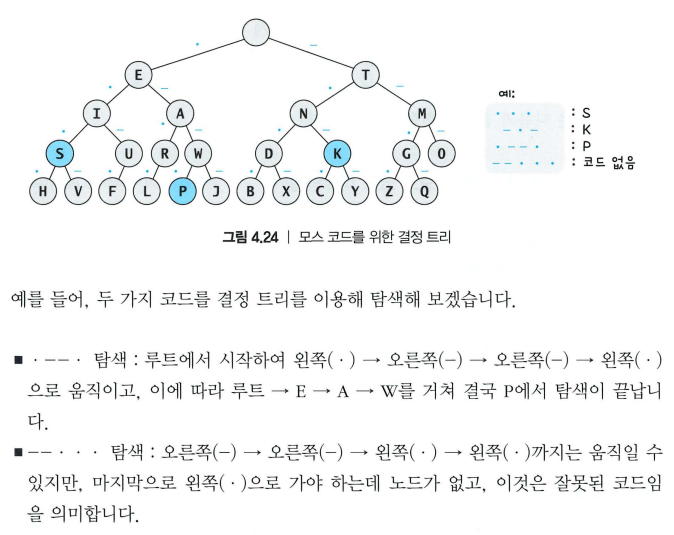
모스 코드 결정 트리 만들기
(1) 빈 루트 노드를 만들고 모스 코드표의 각 문자를 하나씩 트리에 추가함
(2) 문자를 추가할 때 루트부터 시작해 트리를 타고 내려감, 만약 타고 내려갈 자식 노드라 None이면 새로운 노드를 추가함, 노드만 추가할 뿐이고 그 노드의 문자는 결정할 수 없음
(3) 마지막 코드의 노드에 도달하면 그 노드에 문자를 할당함

def make_morse_tree()
  root = BTNode(None, None, None)
  for tp in table:
    code = tp[1]
    node = root
    for c in code:
      if c == '`':
        if node.left == None:
          node.left = BTnode(None, None, None)
        node = node.left
      elif c == '-':
        if node.right == None:
          node.right = BTNode(None, None, None)
        node = node.right
    node.data = tp[0]
  return root

결정 트리를 이용한 디코딩

def decode(root, code):
  node = root
  for c in code:
    if c == '`': node = node.left
    elif c == '-': node = node.right
  return node.data

n개의 노드를 갖는 포화 이진 트리라면, $log_2n$ 에 비례하는 비교 필요

테스트 프로그램

코드

morseCodeTree = make_morse_tree() 
str = input("입력 문장 : ")
mlist = []
for ch i n str:
  code = encode(ch)
  mlist.append(code)
print("Morse Code: ", mlist)
print("Decodi ng : ", end=")
for code in mlist:
  ch = decode(morseCodeTree, code)
  print(ch, end=' ')
print()

실행 결과

입력 문장 : GAMEOVER
Morse Code: ['--.', '.-'. '--', '.', '---', '...-', '.', '.-.']
Decoding : GAMEOVER

Quiz

-.. .- - .-

TREE

MEE

04-5 수식 트리

수식 트리

산술식을 트리 형태로 표현한 이진 트리

수식 트리의 계산

어떤 연산자를 계산하려면 자식 노드의 계산이 반드시 끝나야 함 -> 후위순회

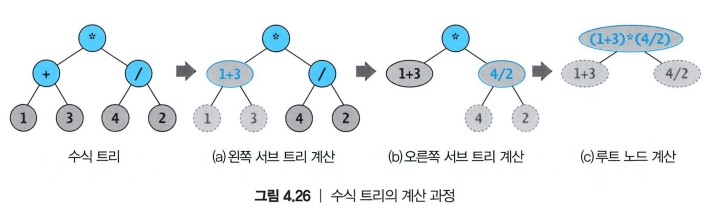
def evaluate(node):
  if node is None:
  return 0
  elif node.isLeaf():
    return node.data
  else:
    op1 = evaluate(node.left)
    op2 = evaluate(node.right)
    if node.data == '+': return op1 + op2
    elif node.data == '-': return op1 - op2
    elif node.data == '*': return op1 * op2
    elif node.data == '/': return op1 / op2

수식의 표현 방법

후위표기의 장점

괄호를 사용하지 않아도 계산 순서를 알 수 있음
식 자체에 우선순위가 이미 포함되어 있기 때문에 연산자의 우선순위를 생각할 필요가 없음
수식을 읽으면서 바로 계산할 수 있음

수식 트리 만들기

전위표기 식으로 수식 트리 만들기

맨 앞에서 뒤로 읽으면서 처리함
입력 수식: * + 1 3 / 4 2

* 첫 항목*은 수식 트리의 루트 노드가 됨
+ 이전 항목*이 연산자이므로 +는 *의 왼쪽 자식이 됨
1 이전 항목+이 다시 연산자이므로 1은 +의 왼쪽 자식이 됨
3 이전 항목1이 피연산자이므로 3은 이전 연산자+의 두 번째 피연산자가 됨, 두 번째 피연산자가 처리되었으므로 +을 루트로 하는 서브 트리는 완성됨
/ 이제 /는 이전 연산자 *의 오른쪽 자식이 됨
4 이전 연산자의 왼쪽 자식이 됨
2 이전 연산자의 오른쪽 자식이 됨

후위표기 식으로 수식 트리 만들기

맨 뒤에서 앞으로 읽으면서 처리
입력 수식: 1 3 + 4 2 / *

* 끝 항목*은 수식 트리의 루트 노드가 됨
/ 이전 항목*이 연산자이므로 /는 *의 오른쪽 자식이 됨
2 이전 항목/이 다시 연산자이므로 2은 +의 왼쪽 자식이 됨
4 이전 항목2이 피연산자이므로 4은 이전 연산자/의 첫 번째 피연산자가 됨, 피 연산자들이 모두 처리되었으므로 /를 루트로 하는 서브 트리는 완성됨
+ 이제 +는 이전 연산자 *의 왼쪽 자식이 됨
3 이전 연산자의 오른쪽 자식이 됨
1 이전 연산자의 왼쪽 자식이 됨

def buildETree(expr):
  if len(expr) == 0:
    return None
  token = expr.pop() 
  if token in "+-*/"
    node = BTNode(token)
    node.right= buildETree(expr)
    node.left = buildETree(expr)
    return node
  else:
    return BTNode(float(token))

테스트 프로그램

코드

str = input("입력(후위표기): ")
expr = str.split()
print("토큰분리 (expr): ", expr)
root = buildETree(expr)
print('\n 전위순회: ', end=''); preorder(root)
print('\n 중위순회: ' , end=''); inorder(root)
print('\n 후위순회: ', end=''); postorder(root)
print('\n 계산 결과 : ', evaluate(root))

실행 결과

입력(후위표기) : 1 3 + 4 2 / *
토큰분리(expr) : ['1', '3', '+', '4', '2', '/', '*']
전위 순회: ( * ( + ( 1.0 ) ( 3.0 ) ) ( / ( 4.0 ) ( 2.0 ) ) )
중위 순회: 1.0 + 3.0 * 4.0 / 2.0  
후뤼 순회: 1.0 3.0 + 4.0 2.0 / *
계산 결과: 8.0

Quiz
/
2 + 8 4
1 3
6

연습 문제

01

class NodeNLink:
    def __init__(self, value):
        self.value = value
        self.links = []  # 연결 리스트를 이용한 링크 저장

    def add_link(self, node):
        self.links.append(node)

02

class NodeLeftChildRightSibling:
    def __init__(self, value):
        self.value = value
        self.left_child = None
        self.right_sibling = None

03

def count_leaf_nodes(root):
    if not root:
        return 0
    if not root.left and not root.right:
        return 1
    return count_leaf_nodes(root.left) + count_leaf_nodes(root.right)

04

MORSE_CODE_DICT = {
    'A': '.-', 'B': '-...', 'C': '-.-.', 'D': '-..', 'E': '.', 'F': '..-.', 'G': '--.', 'H': '....', 'I': '..',
    'J': '.---', 'K': '-.-', 'L': '.-..', 'M': '--', 'N': '-.', 'O': '---', 'P': '.--.', 'Q': '--.-', 'R': '.-.',
    'S': '...', 'T': '-', 'U': '..-', 'V': '...-', 'W': '.--', 'X': '-..-', 'Y': '-.--', 'Z': '--..',
    '1': '.----', '2': '..---', '3': '...--', '4': '....-', '5': '.....', '6': '-....', '7': '--...', '8': '---..', '9': '----.', '0': '-----',
    '.': '.-.-.-', ',': '--..--', '?': '..--..', '/': '-..-.', '-': '-....-', '(': '-.--.', ')': '-.--.-'
}
REVERSE_MORSE_CODE_DICT = {v: k for k, v in MORSE_CODE_DICT.items()}

def encode_morse(text):
    return ' '.join(MORSE_CODE_DICT.get(char.upper(), '') for char in text)
    
def decode_morse(morse_code):
    return ''.join(REVERSE_MORSE_CODE_DICT.get(code, '') for code in morse_code.split(' '))

05

def precedence(op):
    """연산자의 우선순위를 반환"""
    if op in ('+', '-'):
        return 1
    if op in ('*', '/'):
        return 2
    if op == '^':  # 거듭제곱
        return 3
    return 0

def infix_to_postfix(expression):
    """중위표기식을 후위표기식으로 변환"""
    output = []
    stack = []
    
    for token in expression.split():
        if token.isnumeric():  # 숫자는 바로 출력
            output.append(token)
        elif token == '(':  # 왼쪽 괄호는 스택에 push
            stack.append(token)
        elif token == ')':  # 오른쪽 괄호는 '(' 만날 때까지 pop
            while stack and stack[-1] != '(':
                output.append(stack.pop())
            stack.pop()  # '(' 제거
        else:  # 연산자
            while stack and precedence(stack[-1]) >= precedence(token):
                output.append(stack.pop())
            stack.append(token)

    # 스택에 남아있는 연산자 출력
    while stack:
        output.append(stack.pop())
    
    return ' '.join(output)

# 테스트
expr = "3 + 5 * ( 2 - 8 )"
print(infix_to_postfix(expr))  # 출력: 3 5 2 8 - * +

찬은

이전 포스트

[자료구조와 알고리즘 with 파이썬] 03 리스트

다음 포스트

[자료구조와 알고리즘 with 파이썬] 04 트리