[자료구조와 알고리즘 with 파이썬] 05 알고리즘 개요

찬은·2025년 4월 8일

알고리즘 자료구조와 알고리즘 with 파이썬

자료구조와 알고리즘 with 파이썬

목록 보기

5/10

05-1 알고리즘이란?
05-2 알고리즘의 성능 분석

—-

05-1 알고리즘이란?

알고리즘의 정의와 조건

알고리즘

주어진 문제를 해결하기 위한 단계적인 절차

명령어

컴퓨터에서 수행되는 문장
프로그래밍 언어와 상관없이 문제 해결 절차를 나타내는 명령어의 집합

알고리즘의 조건

입력: 모호하지 않고 잘 정의된 입력
출력: 명확히 정의된 1개 이상의 출력
명확성: 각 명령어의 의미가 모호하지 않고 명확해야 함
유한성: 한정된 수의 단계 후에는 반드시 종료되어야 함
언어 독립성: 프로그래밍 언어와 상관 없음
유효성: 명령어 들은 현재 실행 가능한 연산이어야 함

알고리즘의 기술 방법

영어나 한국어와 같은 자연어를 사용하는 방법
흐름도(flowchart)로 표시하는 방법
특정한 프로그래밍 언어(C언어, Java, 파이썬)의 코드로 나타내는 방법
유사 코드(pseudo-code)로 기술하는 방법

자연어 표현

표현이 자유롭고 편리함
문장의 의미가 애매해질 수 있음

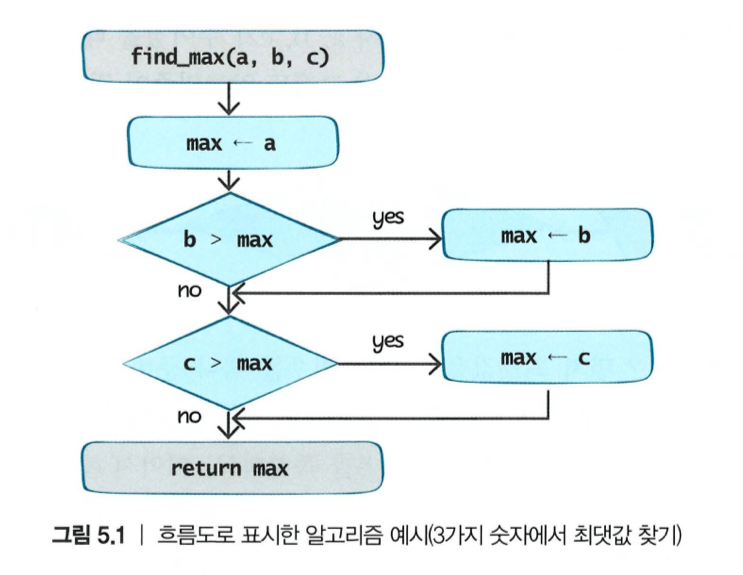
find_max(a, b, c)
  a를 최댓값을 저장하는 변수 max에 복사합니다.
  만약 b가 max보다 크면 b를 max에 복사합니다.
  만약 c가 max보다 크면 c를 max에 복사합니다.
  max를 반환합니다.

흐름도 표현

알고리즘의 절차들을 가장 정확하게 표현할 수 있어서 명세서 등에 자주 사용됨
알고리즘이 조금만 길어도 그림이 너무 복잡해져 혼란스러워짐

특정 프로그래밍 언어 표현

특정 프로그래밍 언어로 기술하면 알고리즘을 실행해 볼 수 있어 편리함
프로그래밍 언어의 특징에 따라 불필요한 표현들이 알고리즘에 포함되기 때문에, 알고리즘의 핵심을 이해하는 데 방해됨

int find_max(int a, int b, int c){
  int max = a;
  if(b > max A[i]) {
    max = b;
  }
  if(c > max A[i]){
    max = c;
  }
  return max; // ?

유사코드(pseudo code) 표현

프로그래밍 언어에서 발생하는 많은 불필요한 표현을 생략할 수 있음

find_max(a, b, c)
  max <- a
  if b > max then
    max <- b
  if c > max then
    max <- c
  return max

파이썬을 이용한 표현

파이썬은 알고리즘을 바로 실행해 확인할 수 있음

def find_max(a, b, c):
  max = a
  if b > max:
    max = b
  if c > max:
    max = c
  return max

—-

05-2 알고리즘의 성능 분석

성능 비교를 위한 다양한 기준

연산량: 알고리즘이 얼마나 적은 연산을 수행하는가? -> 시간효율성
메모리 사용량: 얼마나 적은 메모리 공간을 사용하는가? -> 공간효율성

실행 시간 측정 방법

import time
start = time.time()
testAlgorithm(input)
-
end = time.time()
print(“실행시간 = “, end-start)

단점

알고리즘을 구현하는데 부담이 될 수 있음
알고리즘 결과 비교를 위해 반드시 같은 조건의 하드웨어 사용해야 함
프로그래밍 언어나 운영체제와 같은 소프트웨어 환경도 동일해야 함
실행되지 않은 입력에 대해서는 실행 시간을 주장할 수 없음

복잡도 분석 방법

복잡도 분석

구현하지 않고 알고리즘의 시간 복잡도와 공간 복잡도를 구해 성능을 비교함

clac_sum1(n) # 반복문 이용
  sum <- 0
  for i <- 1 to n then
    sum <- sum + 1
  return sum

calc_sum2(n) # 공식 이용
  sum <- n * (n+1) / 2
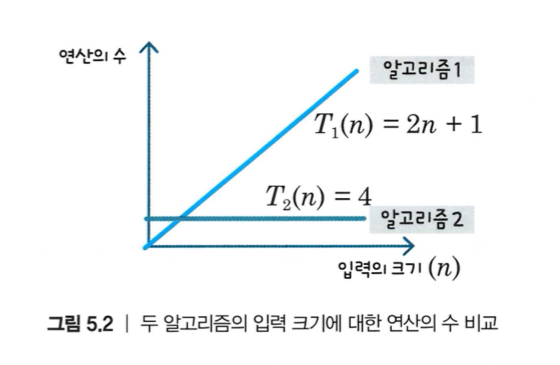
  return sum

복잡도 함수

연산의 실행 횟수를 입력의 크기 n에 대한 함수 형태 $T(n)$ 으로 나타냄

알고리즘 2는 입력의 크기 n과 관계 없이 같은 수의 연산이 실행됨

알고리즘 1은 입력의 크기 n에 비례하는 수의 연산이 실행됨

n이 커질수록 알고리즘 2가 알고리즘 1보다 훨씬 효율적임

복잡도의 점근적 표기

증가속도 표현

빅오(big-O) 표기법

$O(g(n))$ 은 증가속도가 $g(n)$ 과 같거나 낮은 모든 복잡도 함수를 포함하는 집합(상한)
$O(n^2)$ 는 어떤 경우에도 $n^2$ 에 비례하는 시간에는 완료된다는 것을 의미함

빅오메가(big-omega) 표기법

$\Omega(g(n))$ 은 증가속도가 $g(n)$ 과 같거나 높은 모든 복잡도 함수를 포함함(하한)
$\Omega(n^2)$ 는 아무리 빨리 처리하더라도 $n^2$ 에 비례하는 시간 이상은 반드시 걸린다는 것을 의미함

빅세타(big-theta) 표기법

$\theta(g(n))$ 은 증가속도가 $g(n)$ 과 같은 복잡도 함수들만을 포함함(상한/하한)

최선, 최악, 평균적인 효율성

같은 알고리즘도 입력의 종류 또는 구성에 따라 다른 특성의 실행 시간을 보일 수 있음
따라서, 입력의 특징에 따라 3가지 경우로 나누어 평가할 수 있음
- 최선의 경우(best case): 실행 시간이 가장 적은 경우를 말하는데, 알고리즘 분석에서는 큰 의미가 없음
- 평균적인 경우(average case): 알고리즘의 모든 입력을 고려하고 각 입력이 발생할 확률을 고려한 평균적인 실행 시간을 의미하는데, 정확히 계산하기 어려움
- 최악의 경우(worst case): 입력의 구성이 알고리즘의 실행 시간을 가장 많이 요구하는 경우를 말하고, 가장 중요하게 사용됨

예: 리스트에서 최댓값을 찾는 알고리즘

리스트에서 ‘최댓값’을 찾아 반환하는 간단한 알고리즘을 작성하고 복잡도 분석함

def find_max(A):
  n = len(A)
  max = A[0]
  for i in range(n):
    if A[i] > max:
      max = A[i]
  return max

이 알고리즘에서 입력의 크기는 리스트의 크기가 됨
4행의 반복문이 총 n번 반복되므로 반복문 내부인 5행은 n번 처리 -> $T(n) = n$
$O(n)$ 에 속함
리스트의 크기가 같다면 리스트의 내용 상관없이 반복되는 횟수는 같음 -> 항상 같은 연산이 필요함

예: 리스트에서 어떤 값을 찾는 알고리즘

def find_key(A, key):
  n = len(A)
  for i in range(n):
    if A[i] == key:
      return i
  return -1

순차 탐색
입력의 크기는 리스트의 크기이고, 4행이 가장 많이 처리되는 문장임
입력의 구성에 따라 검사 횟수가 달라짐
- 최선의 경우: A의 첫 번째 요소가 key와 같은 경우 -> $T_{best}(n) = 1$ , $O(1)$
- 최악의 경우: key가 리스트에 없거나 맨 뒤에 있는 경우 -> $T_{worst}(n) = n$ , $O(n)$
- 평균적인 경우: 모든 숫자가 균일하게 탐색되는 상황을 평균이라고 가정 $T_{avg}(n) = \frac{1+2+ … + n}{n} = \frac{n(n+1)/2}{n} = \frac{n+1}{2} \in O(n)$
최악의 경우에 대한 복잡도가 가장 중요함

찬은

이전 포스트

[자료구조와 알고리즘 with 파이썬] 04 트리

다음 포스트